
松廼屋|論点解説 薬剤師国家試験対策ノート問106-178【薬剤】論点:Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移
第106回薬剤師国家試験|薬学理論問題 /
問178
一般問題(薬学理論問題)【薬剤】
問106-178
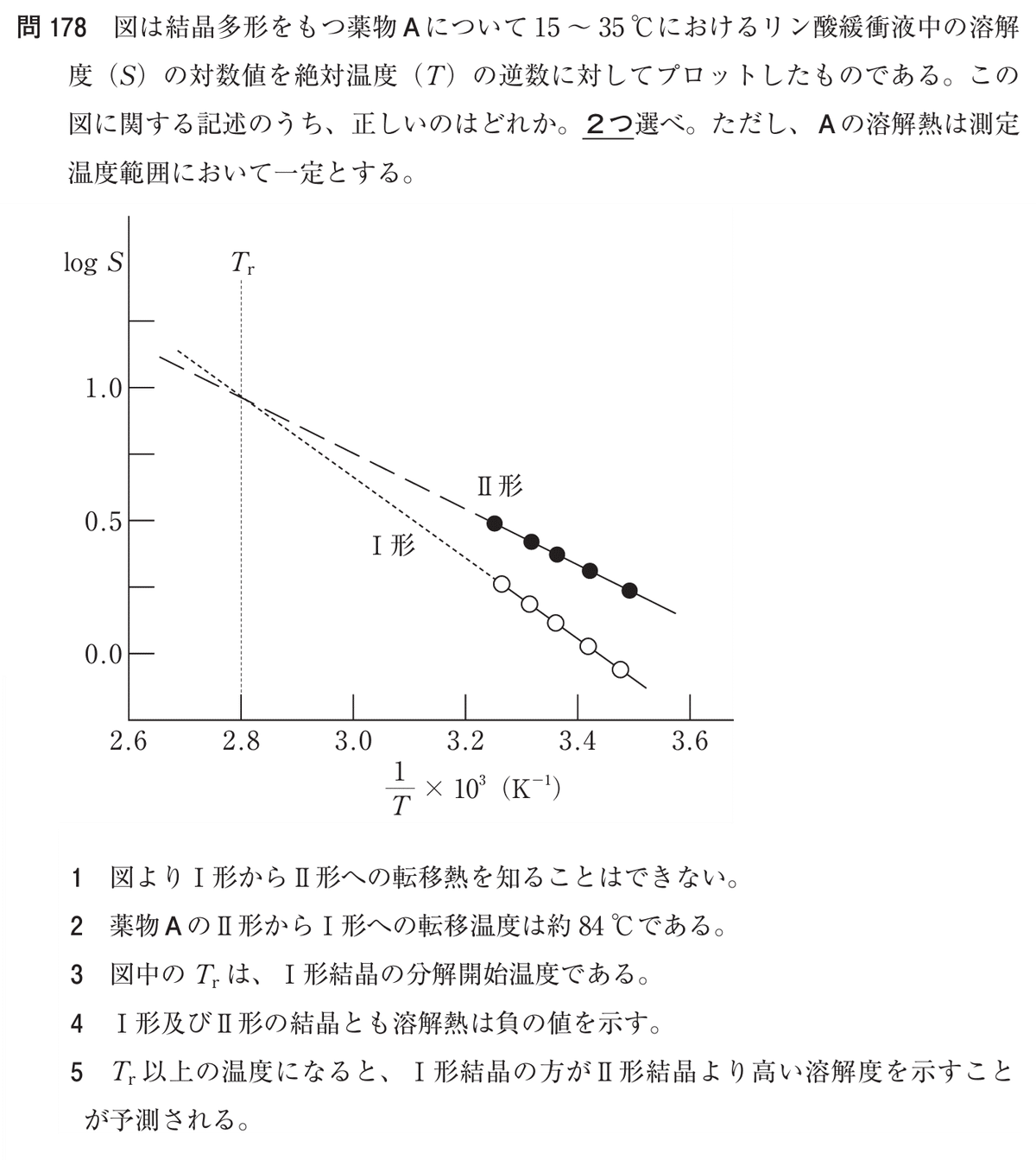
Q. 図は結晶多形をもつ薬物Aについて15~35℃におけるリン酸緩衝液中の溶解度(S)の対数値を絶対温度(T)の逆数に対してプロットしたものである。この図に関する記述のうち、正しいのはどれか。2つ選べ。ただし、Aの溶解熱は測定温度範囲において一定とする。
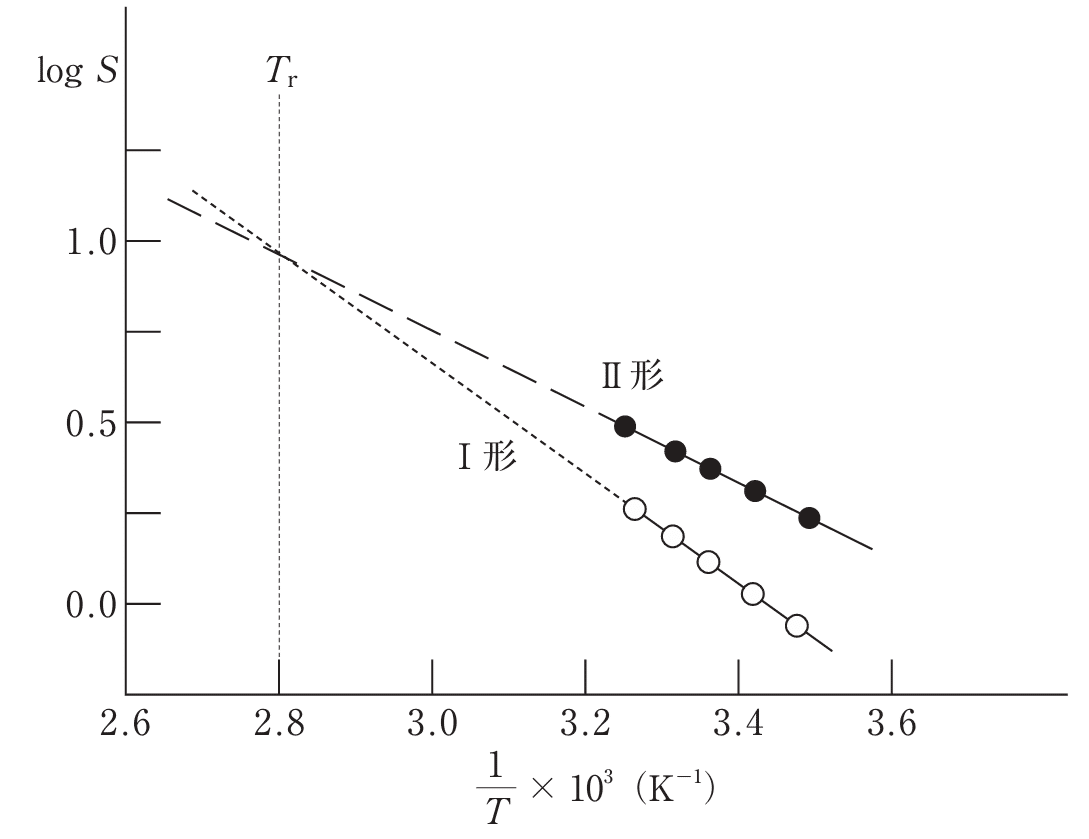
■選択肢
1. 図よりⅠ形からII形への転移熱を知ることはできない。
2. 薬物AのII形からⅠ形への転移温度は約84℃である。
3. 図中のTrは、Ⅰ形結晶の分解開始温度である。
4. Ⅰ形及びII形の結晶とも溶解熱は負の値を示す。
5. Tr以上の温度になると、Ⅰ形結晶の方がII形結晶より高い溶解度を示すことが予測される。
こんにちは!薬学生の皆さん。
Mats & BLNtです。
matsunoya_note から、薬剤師国家試験の論点解説をお届けします。
苦手意識がある人も、この機会に、薬学理論問題【薬剤】を一緒に完全攻略しよう!
今回は、第106回薬剤師国家試験|薬学理論問題 / 問178、論点:Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移を徹底解説します。
薬剤師国家試験対策ノート NOTE ver.
matsunoya_note|note https://note.com/matsunoya_note
Here; https://note.com/matsunoya_note/n/ncf8f4243cf18
松廼屋|論点解説 薬剤師国家試験対策ノート問106-178【薬剤】論点:Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移
薬剤師国家試験対策には、松廼屋の eラーニング
「薬剤師国家試験対策ノート」
マガジン|薬剤師国家試験対策ノート on note
👉マガジンをお気に入りに登録しよう!
このコンテンツの制作者|
滝沢 幸穂 Yukiho Takizawa, PhD
https://www.facebook.com/Yukiho.Takizawa
お友達や知り合いに、matsunota_note で学習したeラーニングを勧めてみたい方は、いいね!、口コミ、おススメなど、よろしくお願いします!
設問へのアプローチ|
第106回薬剤師国家試験の問178(問106-178)では、Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移に関する知識を問われました。
溶解度と温度の関係におけるVan 't Hoff式
ln S = -Δ H_sol / RT +Δ S_sol / R
ここで、
S は溶解度
R はガス定数
T は絶対温度
計算問題は、慣れです。
手を動かして繰り返し解いてみてください。
2分30秒以内に解けるか、タイマーで時間を測定しながら解いてみると自信がつきます。
出題範囲:
製剤化のサイエンス|製剤の性質|固形材料|
粉体の性質について説明できる。
結晶(安定形及び準安定形)や非晶質、無水物や水和物の性質について説明できる。
固形材料の溶解現象(溶解度、溶解平衡等)や溶解した物質の拡散と溶解速度について説明できる。👈ココ
固形材料の溶解に影響を及ぼす因子(pHや温度等)について説明できる。👈ココ
固形材料の溶解度や溶解速度を高める代表的な製剤的手法を列挙し、説明できる。
薬剤師国家試験 出題基準
出典: 薬剤師国家試験のページ |厚生労働省 (mhlw.go.jp)
出題基準 000573951.pdf (mhlw.go.jp)
今回の解説は、Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移を語らせたら生成AI界で右に出る者はいない Grok 2 mini (beta) の登板です(^^)/
基本的な知識について復習しておきましょう。
■■Grok 2 mini (beta)
結晶多形をもつ薬物におけるVan 't Hoff式の概説
1. Van 't Hoff式の基本概念
Van 't Hoff式は、温度に対する反応の平衡定数の変化を記述する熱力学的な式です。しかし、ここでは溶解度の温度依存性について考えます。溶解度 S は平衡定数 K_sp に相当します。
d ln K_sp / d T =Δ H_sol / RT^2
ここで、
Δ H_sol は溶解エンタルピー
R はガス定数
T は絶対温度
溶解度 S を用いると、以下のように書き換えられます:
d ln S / d T =Δ H_sol / RT^2
2. 結晶多形と溶解度の温度依存性
多形性を持つ薬物では、各多形(例えばI形とII形)の溶解度が温度に対して異なる依存性を持つことがあります。この場合、Van 't Hoff式は各多形に対して適用され、溶解度の温度依存性を解析する際に有用です。
3. Van 't Hoff式を溶解度に適用
溶解度 S を用いたVan 't Hoff式は以下のように表されます:
ln S = -Δ H_sol / RT + C
ここで、 C は積分定数です。温度 T が増加すると、溶解度 S の増加が予測されます。
4. 多形間の溶解度の比較
多形間の溶解度の比較において、Van 't Hoff式は異なる多形間の溶解エンタルピー差を評価するためのツールとなります。例えば、I形とII形の溶解度の温度依存性を比較することで、どちらの多形が特定の温度範囲でより溶解しやすいかを理解できます。
5. 実際の応用と解析
グラフ化:

実験データを ln S vs. 1 / T のグラフにプロットすることで、各多形の溶解度の温度依存性を視覚的に確認できます。傾き m から溶解エンタルピーを求めることができます:
m = -Δ H_sol / R
転移温度の予測:
多形間の溶解度曲線が交わる点は、どちらの多形も同じ溶解度を持つ温度(転移温度)を示します。
6. 結論
結晶多形を持つ薬物におけるVan 't Hoff式は、溶解度の温度依存性を理解し、多形間の溶解度の違いを解析するために非常に有用です。これにより、製薬開発において、特定の温度範囲での安定な多形を選定したり、溶解度を制御する戦略を立てることが可能になります。
Ref.
Atkins, P., & de Paula, J. (2014). Physical Chemistry for the Life Sciences. Oxford University Press.
Van 't Hoff式の詳細な説明とその応用。Grant, D. J. W., & Higuchi, T. (1990). Solubility Behavior of Organic Compounds. Wiley-Interscience.
溶解度の温度依存性と多形に関する理論的背景。Brittain, H. G. (2016). Polymorphism in Pharmaceutical Solids. CRC Press.
薬物の多形性の影響とその解析方法。Pudipeddi, M., & Serajuddin, A. T. M. (2005). "Trends in Solubility of Polymorphs." Journal of Pharmaceutical Sciences, 94(5), 929-939.
多形間の溶解度の違いに関する研究。Hill, T. L. (1986). An Introduction to Statistical Thermodynamics. Dover Publications.
熱力学および統計熱力学の基礎を含む。
これらの文献は、Van 't Hoff式を用いた多形の溶解度解析の理解に役立つ基本的な情報を提供しています。
論点を整理します。
■■Grok 2 mini (beta)
総合的な論点
この問題は、薬物Aの結晶多形(I形とII形)の溶解度に関する温度依存性を解析するものです。
溶解度の温度依存性
溶解度 S は一般的に溶解エンタルピー Δ H_sol と溶解エントロピー Δ S_sol に依存します。溶解度の温度依存性は以下の式で表されます:
ln S = -Δ H_sol / RT + Δ S_sol / R
ここで、
S は溶解度
R はガス定数
T は絶対温度
グラフの解析
グラフのY軸が log S であり、X軸が 1 / T × 10^3 なので、上記の式を対数に変換した形で考えます:
log S = -Δ H_sol / 2.303RT + 定数

このグラフでは、直線の傾き m は以下の関係式から得られます:
m = -Δ H_sol / 2.303R
このグラフでは、傾きが負であることから、溶解エンタルピー Δ H_sol は正の値を持つことが示唆されます。
多形間の転移
Tr はI形とII形の溶解度が等しい温度です。
この点ではエンタルピーとエントロピーが平衡状態に達し、以下の関係が成り立ちます:
Δ G =Δ H - TΔ S = 0
ここで、 Δ G はギブズ自由エネルギー変化です。
問題の論点は薬物Aの結晶多形間の溶解度の温度依存性と、それに伴う熱力学的性質(特に溶解エンタルピーと溶解エントロピー)の理解に基づいています。
各選択肢の論点および解法へのアプローチ方法
選択肢1: 図よりⅠ形からII形への転移熱を知ることはできない。
論点: この選択肢は、溶解度曲線の交点や傾きから直接転移熱(転移エンタルピー)を得ることはできないという主張です。
アプローチ:
グラフから直接転移熱を得るためには、具体的な溶解熱を知る必要がありますが、グラフ自体ではこれは示されていません。
しかし、傾きから溶解エンタルピーを推定し、その差から転移エンタルピーを計算することは可能です。ただし、詳細な数値がなければ正確な転移熱は特定できません。

選択肢2: 薬物AのII形からⅠ形への転移温度は約84℃である。
論点: 転移温度を具体的な数値で示す。
アプローチ:
Trが 1 / T × 10^3 = 2.8 に対応しているので、Tを求めます。
T = 1 / 2.8 × 10^3 ≒ 357.14 K。
これをセルシウス度に変換すると
357.14 - 273.15 ≒ 84 ℃。

選択肢3: 図中のTrは、Ⅰ形結晶の分解開始温度である。
論点: Trを分解開始温度と関連付けている。
アプローチ:
Trは溶解度が等しくなる温度であり、分解開始温度とは異なります。
分解開始温度は通常、別の実験(例えばDSC)によって決定されます。

選択肢4: Ⅰ形及びII形の結晶とも溶解熱は負の値を示す。
論点: 溶解エンタルピーが負であるという主張。
アプローチ:
傾きが負であることから、溶解エンタルピー Δ H_sol は正の値を持つことが示唆されました。
溶解エンタルピーが負というのは、溶解がエネルギーを放出する過程であることを意味しますが、ここでの傾きからは正しいとは言えません。

選択肢5: Tr以上の温度になると、Ⅰ形結晶の方がII形結晶より高い溶解度を示すことが予測される。
論点: 温度がTr以上でどちらが高い溶解度を示すか。
アプローチ:
グラフではTr以上でI形の溶解度がII形より高いことが示されています。
この予測はグラフの傾きと交点から直接導かれます。

各選択肢の論点および解法へのアプローチ方法
深掘り
選択肢1: 図よりⅠ形からII形への転移熱を知ることはできない。
論点の詳細:
転移熱とは、ある結晶形(例えばI形)から別の結晶形(II形)への転移に必要なエネルギー(エンタルピー変化)を指します。
この転移熱を直接グラフから得ることは、実際には難しいか不可能です。なぜなら、グラフは溶解度の温度依存性を示しており、転移熱そのものを直接描写しているわけではないからです。

アプローチ方法:
グラフの傾きから溶解エンタルピーの推定:
傾き m から溶解エンタルピー Δ H_sol を推定できます:
m = -Δ H_sol / 2.303R
ここで、 R はガス定数(8.314 J/mol·K)です。
傾きの絶対値を比較して、I形とII形の溶解エンタルピーの違いを知ることはできますが、詳細な数値を知るためには具体的な傾きの数値が必要です。
転移エンタルピーの計算:
転移エンタルピー Δ H_tr は、以下のように計算できます:
Δ H_tr =Δ H_sol,II -Δ H_sol,I
ここで、 Δ H_sol,II と Δ H_sol,I はそれぞれII形とI形の溶解エンタルピーです。
結論:
グラフは溶解度の温度依存性を示すものであり、転移熱を直接得るための情報は含まれていません。したがって、この選択肢の主張は正しいです。
選択肢2: 薬物AのII形からⅠ形への転移温度は約84℃である。
論点の詳細:
転移温度は、ある相(ここではII形)が別の相(I形)に変わる温度を指します。グラフ上では、溶解度が等しくなる点がこの転移温度に対応します。
アプローチ方法:
転移温度の特定:
グラフでは、X軸が 1 / T × 10^3 で、Y軸が log S です。転移点 Tr は 1 / T × 10^3 = 2.8 に対応しています。
絶対温度 T の計算:
この情報を使って絶対温度 T を求めます:
T = 1 / 2.8 × 10^-3 ≒ 357.14 K
ここで、357.14Kをセルシウス度に変換します:
T_℃ = 357.14 K - 273.15 K ≒ 84 ℃
結論:
したがって、選択肢2の主張「薬物AのII形からI形への転移温度は約84℃である。」は、グラフの情報に基づいて正しいです。グラフから導かれる転移温度が約84℃であることは、計算により確認できます。
選択肢3: 図中のTrは、Ⅰ形結晶の分解開始温度である。
論点の詳細:
分解開始温度は、物質が熱分解を始める温度を指します。これは通常、熱重量分析(TGA)や差熱走査カロリメトリー(DSC)などの手法で測定されます。
アプローチ方法:
グラフのTrの意味:
TrはI形とII形の溶解度が等しくなる温度を示しており、これは溶解度の温度依存性の観点から重要です。具体的には、Trは以下の条件を満たします:
log S_I = log S_II
ここで、 S_I と S_II はそれぞれI形とII形の溶解度です。
分解開始温度との関連性の欠如:
分解開始温度は物質が分解し始める温度であり、これは溶解度の温度依存性とは直接関連しません。
グラフ上のTrは、I形とII形の溶解度が同じになる温度です。
結論:
選択肢3の主張「図中のTrは、Ⅰ形結晶の分解開始温度である。」は、グラフの情報から直接導かれるものではありません。したがって、この主張は誤りです。Trは多形間の溶解度が等しくなる温度であり、分解開始温度とは異なります。
選択肢4: Ⅰ形及びII形の結晶とも溶解熱は負の値を示す。
論点の詳細:
溶解熱(溶解エンタルピー Δ H_sol )は、ある物質が溶液中に溶解する際に吸収または放出される熱量を指します。溶解熱が負の場合、それはエネルギーを放出する過程(エキソテルミック)です。
アプローチ方法:
溶解度の温度依存性と溶解エンタルピー:
グラフのY軸が log S であり、X軸が 1 / T 、傾き m は以下の関係式から求まります:
m = -Δ H_sol / 2.303RT
ここで、傾きが負であることを意味します。
傾きの解釈:
傾きが負の値を示すのは、溶解度が温度上昇に伴って増加することを示しています。
これは、溶解エンタルピー Δ H_sol が正の値を持つことを示唆します。なぜなら、溶解がエネルギーを吸収する(吸熱;エンドテルミック)過程である場合、温度が上がるほど溶解度が増加するからです。
溶解熱の負の値の解釈:
溶解熱が負の値を示すというのは、溶解がエネルギーを放出する過程であることを意味します。すなわち、溶解度が温度低下に伴って増加する場合です。
しかし、グラフの傾きが負であることから、溶解度は温度上昇に伴って増加しています。これは溶解がエネルギーを吸収する過程であることを示しています。
結論:
選択肢4の主張「Ⅰ形及びII形の結晶とも溶解熱は負の値を示す。」は、グラフの傾きと溶解度の温度依存性から見て誤りです。
溶解エンタルピーが負の値を持つというのは、溶解が発熱(エキソテルミック)であることを意味しますが、グラフから見て溶解は吸熱(エンドテルミック)であることが示唆されています。
選択肢5: Tr以上の温度になると、Ⅰ形結晶の方がII形結晶より高い溶解度を示すことが予測される。
論点の詳細:
選択肢5は、特定の温度(Tr)以上でI形の溶解度がII形より高いことを示唆しています。これは、多形間の溶解度の温度依存性に基づいた予測です。
アプローチ方法:
グラフの傾きと溶解度の温度依存性:
グラフの傾きが負であることは、溶解度が温度と共に増加することを示しています。具体的には、I形の傾きの絶対値がII形より大きいため、温度上昇に伴ってI形の溶解度の増加速度がII形より速いことが示唆されます。
Trの決定:
TrはI形とII形の溶解度が等しくなる温度であり、ここでは 1 / T × 10^3 = 2.8 に対応します。Tr以上の温度では、I形とII形の溶解度の差が増加します。
予測の検証:
グラフの傾きから、Tr以上の温度ではI形の溶解度の方がII形より高いことが予測されます。具体的には、以下の式で表されます:
log S_I > log S_II for T > Tr
この関係式を満たすためには、I形の溶解度の温度依存性(傾き)がII形より強い必要があります。これはグラフの傾きの比較からも明らかです。
結論:
選択肢5の主張「Tr以上の温度になると、Ⅰ形結晶の方がII形結晶より高い溶解度を示すことが予測される。」は、グラフの傾きと溶解度の温度依存性に基づいて正しいです。グラフの傾きから見て、Tr以上の温度ではI形の溶解度がII形より高いと予測されることが確認できます。
以上のステップで、選択肢5が正しいことが示されました。
8. Ref.
以下は、問題の解説に関連する科学的根拠や一般的な知識を提供する文献のリストです。これらの文献は、溶解度の温度依存性、結晶多形、および熱力学の基本原理に関する情報を提供します。
Atkins, P., & de Paula, J. (2014). Physical Chemistry for the Life Sciences. Oxford University Press.
溶解度の温度依存性と熱力学の基本原理についての詳細な説明。
Grant, D. J. W., & Higuchi, T. (1990). Solubility Behavior of Organic Compounds. Wiley-Interscience.
溶解度の理論と実際のアプローチに関する包括的なレビュー。
Brittain, H. G. (2016). Polymorphism in Pharmaceutical Solids. CRC Press.
薬物の結晶多形についての詳細な議論。
Haleblian, J., & McCrone, W. (1969). "Pharmaceutical Applications of Polymorphism." Journal of Pharmaceutical Sciences, 58(8), 911-929.
多形が薬物の物性に与える影響についての古典的な論文。
Giron, D. (1995). "Thermal Analysis and Calorimetric Methods in the Characterisation of Polymorphs and Solvates." Thermochimica Acta, 248, 1-59.
熱分析を用いた多形の特性評価についてのレビュー。
Pudipeddi, M., & Serajuddin, A. T. M. (2005). "Trends in Solubility of Polymorphs." Journal of Pharmaceutical Sciences, 94(5), 929-939.
多形間の溶解度の違いとその傾向についての論文。
Hill, T. L. (1986). An Introduction to Statistical Thermodynamics. Dover Publications.
統計熱力学の基本原理とその応用について。
Connors, K. A. (1990). Chemical Kinetics: The Study of Reaction Rates in Solution. Wiley-VCH.
溶液中での反応速度と溶解度の関係についての議論を含む。
これらの文献は、問題の背景となる科学的知識を提供し、溶解度の温度依存性や多形の理解に役立ちます。
選択肢1の論点および解法へのアプローチ方法
より詳細に!!
選択肢1: 図よりⅠ形からII形への転移熱を知ることはできない。
詳細なアプローチ:
グラフの傾きから溶解エンタルピーの推定:
グラフの傾き m は以下の式で与えられます:
m = -Δ H_sol / 2.303RT
ここで、
Δ H_sol は溶解エンタルピー
R はガス定数(8.314 J/mol·K)
T は温度

与えられたデータを使って各結晶の傾きを計算します。
I型の傾き:
m_I = 0.01 - 0.35 / 3.4 - 3.2 = -0.34 / 0.2 = -1.7
したがって、溶解エンタルピー Δ H_sol,I は:
Δ H_sol,I = -2.303 × 8.314 × 1.7 × 10^3 ≒ 32.33 kJ/mol
II形の傾き:
m_II = 0.35 - 0.55 / 3.4 - 3.2 = -0.20 / 0.2 = -1.0
したがって、溶解エンタルピー Δ H_sol,II は:
Δ H_sol,II = -2.303 × 8.314 × 1.0 × 10^3 ≒ 19.17 kJ/mol
転移エンタルピーの計算:
転移エンタルピー Δ H_tr は、以下のように計算できます:
Δ H_tr =Δ H_sol,II -Δ H_sol,I
これを代入すると:
Δ H_tr = 19.17 kJ/mol - 32.33 kJ/mol ≒ -13.16 kJ/mol
しかし、この計算には問題があります。
グラフから直接転移熱を正確に導くには、溶解エンタルピーの差だけでなく、他の熱力学的パラメータ(例えば溶解エントロピー)も必要です。
結論:
グラフから傾きを使って溶解エンタルピーを推定することはできましたが、転移熱を正確に知るためには詳細な溶解度データと温度依存性が必要です。したがって、選択肢1の主張「図よりⅠ形からII形への転移熱を知ることはできない。」は、グラフの情報のみから転移熱を正確に得ることができないという点で正しいです。
以上で、論点整理を終わります。
理解できたでしょうか?
大丈夫です。
完全攻略を目指せ!
はじめましょう。
薬剤師国家試験の薬学理論問題【薬剤】からVan 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移を論点とした問題です。
なお、以下の解説は、著者(Yukiho Takizawa, PhD)がプロンプトを作成して、その対話に応答する形でGPT4o & Copilot 、Gemini 1.5 Pro、またはGrok 2 (beta) が出力した文章であって、著者がすべての出力を校閲しています。
生成AIの製造元がはっきりと宣言しているように、生成AIは、その自然言語能力および取得している情報の現在の限界やプラットフォーム上のインターフェースのレイト制限などに起因して、間違った文章を作成してしまう場合があります。
疑問点に関しては、必要に応じて、ご自身でご確認をするようにしてください。
松廼屋|論点解説 薬剤師国家試験対策ノート問106-178【薬剤】論点:Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移|matsunoya (note.com)
Here we go.
第106回薬剤師国家試験|薬学理論問題 /
問178
一般問題(薬学理論問題)【薬剤】
問106-178
Q. 図は結晶多形をもつ薬物Aについて15~35℃におけるリン酸緩衝液中の溶解度(S)の対数値を絶対温度(T)の逆数に対してプロットしたものである。この図に関する記述のうち、正しいのはどれか。2つ選べ。ただし、Aの溶解熱は測定温度範囲において一定とする。

■選択肢
1. 図よりⅠ形からII形への転移熱を知ることはできない。
2. 薬物AのII形からⅠ形への転移温度は約84℃である。
3. 図中のTrは、Ⅰ形結晶の分解開始温度である。
4. Ⅰ形及びII形の結晶とも溶解熱は負の値を示す。
5. Tr以上の温度になると、Ⅰ形結晶の方がII形結晶より高い溶解度を示すことが予測される。
■■Grok 2 mini (beta)
薬剤|問 106-178
■論点|Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移
この問題の論点は、溶解度の温度依存性を理解し、多形間の溶解度曲線が交わる点(転移温度)やその温度以上での溶解度の相対的な変化を解析することです。
■解説1|
薬物AのII形からⅠ形への転移温度は約84℃である。(選択肢2)[正しい]

Trは 1 / T × 10^3 = 2.8 に対応し、転移温度 T を求めると:
T = 1 / 2.8 × 10^-3 ≒ 357.14 K
これをセルシウス度に変換すると:
T_℃ = 357.14 K - 273.15 K ≒ 84 ℃
Tr以上の温度になると、Ⅰ形結晶の方がII形結晶より高い溶解度を示すことが予測される。(選択肢5)[正しい]
グラフの傾きが負であり、I形の傾きの絶対値がII形より大きいため、温度上昇に伴ってI形の溶解度の増加速度がII形より速いことが示されています。これにより、Tr以上ではI形の溶解度がII形より高いと予測されます。

■解説2|
以上の計算から、転移温度が約84℃であることが確認されました。これはグラフの情報に基づく正確な導出です。
傾きの絶対値の比較から、I形の溶解度が温度に対してより強く依存することは、溶解エンタルピーの違いを示しており、Tr以上での溶解度の相対的な変化を予測することができます。
■結論|
選択肢2と5は、グラフの情報およびVan 't Hoff式に基づく解析から正しいと結論付けられます。
■補足|
図よりⅠ形からII形への転移熱を知ることはできない。(選択肢1)[誤り]
グラフの傾きから溶解エンタルピーを推定し、それらを比較することで転移熱を計算することが理論上可能です。しかし、実際にはこの情報のみでは転移熱を正確に知ることは難しく、詳細な実験データや他の熱力学的パラメータが必要です。したがって、この選択肢は情報の不足を理由に誤りと見なすことができますが、理論的には転移熱を推定することが可能です。

図中のTrは、Ⅰ形結晶の分解開始温度である。(選択肢3)[誤り]
Trは多形間の溶解度が同じになる温度を示しており、分解開始温度とは直接関連しません。分解開始温度は、物質が分解を開始する温度であり、通常熱重量分析(TGA)や差熱走査カロリメトリー(DSC)などの手法で測定されます。

Ⅰ形及びII形の結晶とも溶解熱は負の値を示す。(選択肢4)[誤り]
溶解熱が負の値を示すというのは、エネルギーを放出する(エキソテルミック)過程を意味します。しかし、グラフの傾きが負であり、溶解度が温度上昇に伴って増加することを示しているため、溶解はエネルギーを吸収する(エンドテルミック)過程であることが示唆されます。したがって、溶解熱が負であるという主張は誤りです。

■Lecture
論点解説
結晶多形をもつ薬物における転移熱の概説
1. 結晶多形の概念
結晶多形(Polymorphism)とは、同じ化学組成を持つ物質が異なる結晶構造を取る現象を指します。薬物においては、多形の違いは溶解度、溶解速度、安定性、生物利用能などに影響を与えるため、製薬業界では重要な概念です。
2. 転移熱の定義
転移熱(または溶解熱、転移エンタルピー)は、ある結晶形から別の結晶形への転移に必要なエンタルピー変化を指します。具体的には、以下の数式で表現できます:
Δ H_tr = H_final - H_initial
ここで、 H_final は最終状態のエンタルピー、 H_initial は初期状態のエンタルピーです。
3. 転移熱の測定と解析
転移熱は差熱走査カロリメトリー(DSC)などの熱分析法で測定されます。DSCでは、エネルギーの吸収または放出を記録し、これによりエンタルピー変化を計算します。
4. 転移熱の理論的背景
転移熱は、以下の熱力学的関係式に基づいています:
Δ G =Δ H - TΔ S
ここで、
Δ G はギブズ自由エネルギーの変化
Δ H はエンタルピー変化
T は絶対温度
Δ S はエントロピー変化
転移が起こるとき、二つの多形間のギブズ自由エネルギーが等しくなる温度 T_tr があります。この温度で:
Δ G = 0 ⇒Δ H_tr = T_trΔ S_tr
5. 多形間のエンタルピー差
多形間のエンタルピー差は、各多形の溶解エンタルピー (Δ H_sol ) を比較することで推定できます。例えば、I形からII形への転移熱は:
Δ H_tr =Δ H_sol,II -Δ H_sol,I
6. 実際の応用と注意点
実験的測定: DSCなどの実験データから転移熱を測定します。
理論的予測: 溶解度の温度依存性や溶解エンタルピーから転移熱を推定することができますが、正確な数値を得るためには詳細な実験データが必要です。
まとめ
結晶多形をもつ薬物における転移熱は、薬物の物理化学的特性や製薬プロセスに影響を与える重要なパラメータです。転移熱は熱分析法により測定され、理論的には溶解エンタルピー差やギブズ自由エネルギー変化に関連しています。製薬開発では、これらの情報を利用して、より安定な多形を選択したり、製剤の安定性を確保したりすることが求められます。
Ref.
Brittain, H. G. (2016). Polymorphism in Pharmaceutical Solids. CRC Press.薬物の多形についての包括的なレビュー。
Haleblian, J., & McCrone, W. (1969). "Pharmaceutical Applications of Polymorphism." Journal of Pharmaceutical Sciences, 58(8), 911-929.
多形の薬学的応用に関する古典的な論文。Giron, D. (1995). "Thermal Analysis and Calorimetric Methods in the Characterisation of Polymorphs and Solvates." Thermochimica Acta, 248, 1-59.
多形の熱分析に関するレビュー。Grant, D. J. W., & Higuchi, T. (1990). Solubility Behavior of Organic Compounds. Wiley-Interscience.
溶解度と多形性の関係についての詳細な議論。Hill, T. L. (1986). An Introduction to Statistical Thermodynamics. Dover Publications.
統計熱力学の基本原理を含む。
これらの文献は、結晶多形と転移熱の理解に役立つ基本的な情報を提供しています。
必須問題の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 必須問題 第106回-第109回 一覧 powered by Gemini 1.5 Pro, Google AI Studio & GPT4, Copilot|matsunoya (note.com)
薬学理論問題【薬剤】(1) の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 薬学理論問題 薬剤(1) 第106回-第109回 31問 powered by GPT4o, Chat GPT|matsunoya (note.com)
お疲れ様でした。
🍰☕🍊
では、問題を解いてみましょう!
すっきり、はっきりわかったら、合格です。
第106回薬剤師国家試験|薬学理論問題 /
問178
一般問題(薬学理論問題)【薬剤】
問106-178
Q. 図は結晶多形をもつ薬物Aについて15~35℃におけるリン酸緩衝液中の溶解度(S)の対数値を絶対温度(T)の逆数に対してプロットしたものである。この図に関する記述のうち、正しいのはどれか。2つ選べ。ただし、Aの溶解熱は測定温度範囲において一定とする。

■選択肢
1. 図よりⅠ形からII形への転移熱を知ることはできない。
2. 薬物AのII形からⅠ形への転移温度は約84℃である。
3. 図中のTrは、Ⅰ形結晶の分解開始温度である。
4. Ⅰ形及びII形の結晶とも溶解熱は負の値を示す。
5. Tr以上の温度になると、Ⅰ形結晶の方がII形結晶より高い溶解度を示すことが予測される。
楽しく!驚くほど効率的に。
https://note.com/matsunoya_note
お疲れ様でした。
🍰☕🍊
またのご利用をお待ちしております。
ご意見ご感想などお寄せくださると励みになりうれしいです。
note からのサポート、感謝します。
今日はこの辺で、
それではまた
お会いしましょう。
Your best friend
Mats & BLNt
このコンテンツ
松廼屋|論点解説 薬剤師国家試験対策ノート問106-178【薬剤】論点:Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移|matsunoya (note.com)
Here; https://note.com/matsunoya_note/n/ncf8f4243cf18
よろしければこちらもどうぞ
このコンテンツの制作者|
滝沢幸穂(Yukiho.Takizawa)phD
■Facebook プロフィール
https://www.facebook.com/Yukiho.Takizawa
■X (Former Twitter) プロフィール 🔒
https://twitter.com/YukihoTakizawa
CONTACT|
mail: info_01.matsunoya@vesta.ocn.ne.jp (Matsunoya Client Support)
tel: 029-872-9676
日々の更新情報など、Twitter @Mats_blnt_pharm から発信しています!
🔒 🐤💕 https://twitter.com/Mats_blnt_pharm
https://note.com/matsunoya_note
note.com 右上の🔍で
( matsunoya_note 🔍 )
松廼屋 Mats.theBASE
https://matsunoya.thebase.in/
サポート感謝します👍
最後までお読みいただきましてありがとうございました。
Here; https://note.com/matsunoya_note/n/ncf8f4243cf18
松廼屋|論点解説 薬剤師国家試験対策ノート問106-178【薬剤】論点:Van 't Hoff式 / 溶解度の温度依存性 / 結晶多形 / 相転移|matsunoya (note.com)
ここから先は
¥ 700
医療、健康分野のリカレント教育における「最強コンテンツ」を note で誰でもいつでも学習できる、 https://note.com/matsunoya_note はそんな場にしたい。あなたのサポートがあれば、それは可能です。サポート感謝します!松廼屋 matsunoya
