
松廼屋|論点解説 薬剤師国家試験対策ノート問107-176【薬剤】論点:well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度
第107回薬剤師国家試験|薬学理論問題 /
問176
一般問題(薬学理論問題)【薬剤】
問107-176
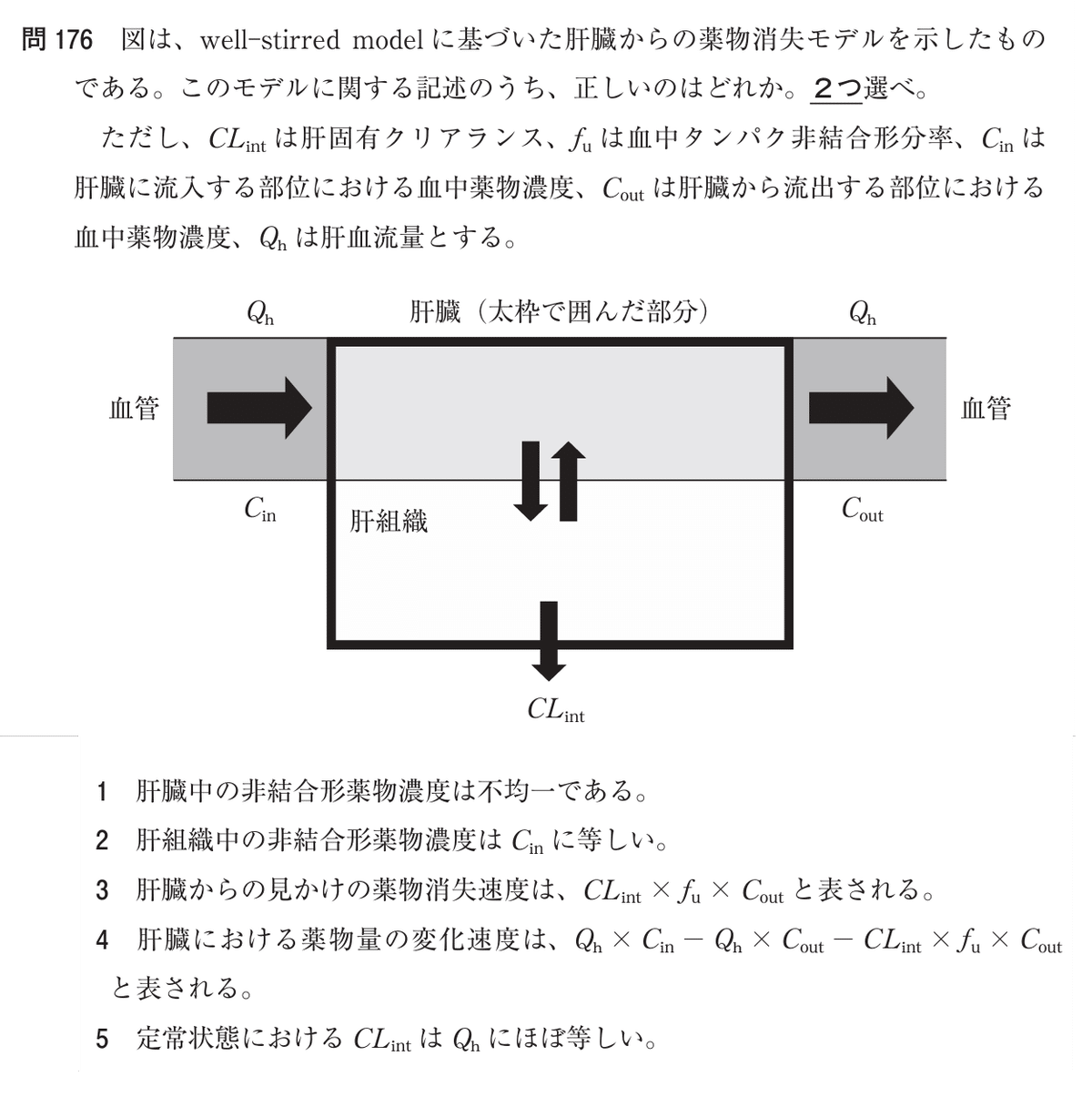
Q. 図は、well-stirred modelに基づいた肝臓からの薬物消失モデルを示したものである。このモデルに関する記述のうち、正しいのはどれか。2つ選べ。ただし、CLintは肝固有クリアランス、fuは血中タンパク非結合形分率、Cinは肝臓に流入する部位における血中薬物濃度、Coutは肝臓から流出する部位における血中薬物濃度、Qhは肝血流量とする。図で肝臓は太枠で囲んだ部分。肝組織は、太枠で囲んだ部分の下半分。

■選択肢
1. 肝臓中の非結合形薬物濃度は不均一である。
2. 肝組織中の非結合形薬物濃度はCinに等しい。
3. 肝臓からの見かけの薬物消失速度は、CLint×fu×Coutと表される。
4. 肝臓における薬物量の変化速度は、Qh×Cin - Qh×Cout - CLint×fu×Coutと表される。
5. 定常状態におけるCLintはQhにほぼ等しい。
こんにちは!薬学生の皆さん。
Mats & BLNtです。
matsunoya_note から、薬剤師国家試験の論点解説をお届けします。
苦手意識がある人も、この機会に、薬学理論問題【薬剤】を一緒に完全攻略しよう!
今回は、第107回薬剤師国家試験|薬学理論問題 / 問176、論点:well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度を徹底解説します。
薬剤師国家試験対策ノート NOTE ver.
matsunoya_note|note https://note.com/matsunoya_note
Here; https://note.com/matsunoya_note/n/n61aa49700eaf
松廼屋|論点解説 薬剤師国家試験対策ノート問107-176【薬剤】論点:well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度
薬剤師国家試験対策には、松廼屋の eラーニング
「薬剤師国家試験対策ノート」
マガジン|薬剤師国家試験対策ノート on note
👉マガジンをお気に入りに登録しよう!
このコンテンツの制作者|
滝沢 幸穂 Yukiho Takizawa, PhD
https://www.facebook.com/Yukiho.Takizawa
お友達や知り合いに、matsunota_note で学習したeラーニングを勧めてみたい方は、いいね!、口コミ、おススメなど、よろしくお願いします!
設問へのアプローチ|
第107回薬剤師国家試験の問176(問107-176)では、well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度に関する知識を問われました。
薬物動態の解析の薬物速度論から、well-stirred model の理解を問う問題です。
well-stirred modelにおける肝クリアランスと肝血流量および肝固有クリアランスおよび血中タンパク非結合形分率との関係の定義は、薬剤師国家試験の出題基準の範囲内と言えます。
ココ👇
組織クリアランス(肝、腎)及び固有クリアランスの意味と、それらの関係について、数式を使って説明できる。
薬剤師国家試験 出題基準
出典: 薬剤師国家試験のページ |厚生労働省 (mhlw.go.jp)
薬物動態の解析|薬物速度論 000573951.pdf (mhlw.go.jp)
線形コンパートメントモデルと、関連する薬物動態パラメータ(全身クリアランス、分布容積、消失半減期、生物学的利用能等)を説明できる。
線形1-コンパートメントモデルに基づいた解析ができる(急速静注・経口投与 [単回及び反復投与]、定速静注)。
体内動態が非線形性を示す薬物の例を挙げ、非線形モデルに基づいた解析ができる。
モーメント解析の意味と、関連するパラメータの計算法について説明できる。
組織クリアランス(肝、腎)及び固有クリアランスの意味と、それらの関係について、数式を使って説明できる。
薬物動態学-薬力学解析(PK-PD解析)について説明できる。
論点を整理します。
■■Grok 2 mini (beta)
総合的な論点

この問題は、肝臓における薬物の消失を説明する「well-stirred model」に基づいています。このモデルは、肝臓が均一にかき混ぜられた単一の区画として扱われ、薬物の濃度が一様であることを前提とします。
具体的には、以下のポイントが重要です:
肝臓の薬物濃度の均一性:肝臓内の薬物濃度が一様であるかどうか。
薬物の消失速度:薬物が肝臓からどのように消失するか、その速度をどのように表現するか。
肝血流と薬物濃度の関係:肝血流量(Qh)が薬物の濃度にどのように影響するか。
薬物の結合と非結合:血中での薬物の結合形と非結合形の比率(fu)が肝臓での消失にどのように影響するか。
2. 各選択肢の論点および解法へのアプローチ方法
選択肢1: 肝臓中の非結合形薬物濃度は不均一である。
論点:
Well-stirred modelでは、肝臓内での薬物濃度が一様であると仮定しています。したがって、非結合形薬物濃度も一様であると考えられます。アプローチ:
文献やモデルの基本原理を参照し、well-stirred modelが均一性を前提としているか確認します。
選択肢2: 肝組織中の非結合形薬物濃度はCinに等しい。
論点:
肝臓に流入する薬物濃度(Cin)と肝組織内の非結合形薬物濃度が等しいかどうか。
Well-stirred modelでは、薬物は即座に均一に分布すると仮定されますが、非結合形のみが直接代謝に関与します。アプローチ:
Cinと肝組織内の非結合形薬物濃度の関係性を検討し、モデルの仮定に基づいて評価します。
選択肢3: 肝臓からの見かけの薬物消失速度は、CLint×fu×Coutと表される。
論点:
この式は、肝臓からの薬物の消失速度を表現しています。CLint(肝固有クリアランス)は非結合形薬物に対してのみ適用され、fu(非結合形分率)を掛けることで全体の消失速度を求めます。アプローチ:
消失速度の定義と、モデルの数学的表現を確認し、この式が正しいか評価します。消失速度 v:

選択肢4: 肝臓における薬物量の変化速度は、Qh×Cin - Qh×Cout - CLint×fu×Coutと表される。
論点:
この式は、薬物の肝内での蓄積と消失を表しています。Qh×Cinは流入量、Qh×Coutは流出量、CLint×fu×Coutは消失量を示します。アプローチ:
肝臓における薬物のマスバランスを確認し、この式が正しいか評価します。肝臓における薬物量の変化速度 dA/dt:

選択肢5: 定常状態におけるCLintはQhにほぼ等しい。
論点:
定常状態では、薬物の消失速度が流入速度と等しくなることがありますが、CLintがQhに等しいとは限りません。高抽出比薬物の場合に近いことがありますが、一般的な特性ではありません。アプローチ:
高抽出比薬物の特性と、肝血流量(Qh)との関係を考慮し、この条件がいつ当てはまるかを検討します。
このように、各選択肢に対してwell-stirred modelの原理と数学的表現を基に評価します。
3. Ref.
以下の文献は、well-stirred modelや肝臓における薬物動態の基礎を理解するための参考資料です:
Pang, K. S., & Rowland, M. (1977). Hepatic clearance of drugs. I. Theoretical considerations of a "well-stirred" model and a "parallel tube" model. Influence of hepatic blood flow, plasma and blood cell binding, and the hepatocellular enzymatic activity on hepatic drug clearance. Journal of Pharmacokinetics and Biopharmaceutics, 5(6), 625-653.
Wilkinson, G. R., & Shand, D. G. (1975). A physiological approach to hepatic drug clearance. Clinical Pharmacology & Therapeutics, 18(4), 377-390.
Rowland, M., & Tozer, T. N. (2011). Clinical Pharmacokinetics and Pharmacodynamics: Concepts and Applications (4th ed.). Philadelphia: Lippincott Williams & Wilkins.
Toutain, P. L., & Bousquet-Mélou, A. (2004). Volumes of distribution. Journal of Veterinary Pharmacology and Therapeutics, 27(6), 441-453.
Davies, B., & Morris, T. (1993). Physiological parameters in laboratory animals and humans. Pharmaceutical Research, 10(7), 1093-1095.
これらの文献は、肝臓の薬物動態モデルや薬物消失速度の計算方法、そして肝血流量(Qh)や肝固有クリアランス(CLint)の関係性についての詳細な説明を含んでいます。
各選択肢の論点を深掘りします。
選択肢1: 肝臓中の非結合形薬物濃度は不均一である。
論点とアプローチ:
Well-stirred modelでは、肝臓内での薬物濃度が一様であると仮定しています。このモデルは、肝組織内で薬物が均等に分配されることを前提としているため、非結合形薬物濃度も一様であるべきです。
解法:
薬物濃度が一様であるため、
Cliver, unbound = Cin × fu
ここで、 Cliver, unbound は肝臓内の非結合形薬物濃度、 Cin は肝臓に流入する薬物濃度、 fu は非結合形分率。
モデルでは、肝臓内での薬物は即座に均一に混合されるとみなされます。したがって、選択肢1の「不均一である」という記述は、well-stirred modelの前提に反するため、正しくないです。
エビデンス:
Pang and Rowland (1977) では、well-stirred modelの詳細な説明があり、肝臓内での一様性が前提として述べられています。
Ref.
Pang, K. S., & Rowland, M. (1977). Hepatic clearance of drugs. I. Theoretical considerations of a "well-stirred" model and a "parallel tube" model. Influence of hepatic blood flow, plasma and blood cell binding, and the hepatocellular enzymatic activity on hepatic drug clearance. Journal of Pharmacokinetics and Biopharmaceutics, 5(6), 625-653.
選択肢2: 肝組織中の非結合形薬物濃度はCinに等しい。
論点とアプローチ:
Well-stirred modelでは、肝臓に流入する薬物濃度(Cin)と肝組織内の薬物濃度は異なります。
肝臓内での代謝や分布により、非結合形薬物濃度は肝臓内の非結合形薬物濃度(Cliver, unbound)として表されます。
解法:
薬物の非結合形濃度 Cliver, unbound は、流入する薬物濃度 Cin と完全に等しいわけではなく、肝臓内での均等混合と代謝を考慮する必要があります。
非結合形薬物濃度は、代謝や結合状態によって変化します。したがって、選択肢2は正しくありません。
肝臓内の非結合形濃度は Cliver, unbound = Cin × fu ではなく、より複雑な動態を反映します。
エビデンス:
Wilkinson and Shand (1975) では、薬物の肝臓内での動態について詳細に述べられ、特に非結合形薬物濃度の理論的考察が行われています。
Ref.
Wilkinson, G. R., & Shand, D. G. (1975). A physiological approach to hepatic drug clearance. Clinical Pharmacology & Therapeutics, 18(4), 377-390.
選択肢3: 肝臓からの見かけの薬物消失速度は、CLint×fu×Coutと表される。
論点とアプローチ:
Well-stirred modelでは、薬物の消失速度は肝臓から流出する薬物濃度(Cout)と肝固有クリアランス(CLint)に加えて、血中非結合形分率(fu)によって決まります。この式は、肝臓からの実際の消失速度を反映します。
解法:
薬物の肝臓からの消失速度 v は、以下の式で表されます:
v = CLint × fu × Cout
CLint は肝臓固有のクリアランスで、非結合形薬物に対する代謝能力を示します。
fu は非結合形分率で、薬物が非結合形で存在する割合を示します。
Cout は肝臓から流出する薬物濃度で、消失速度を計算する際に使用されます。
この式は、薬物の消失速度が肝臓から流出する薬物の濃度に依存していることを示しており、選択肢3は正しいです。
エビデンス:
これらの概念はRowland and Tozer (2011) のテキストで詳細に説明されています。
Ref.
Rowland, M., & Tozer, T. N. (2011). Clinical Pharmacokinetics and Pharmacodynamics: Concepts and Applications (4th ed.). Philadelphia: Lippincott Williams & Wilkins.
選択肢4: 肝臓における薬物量の変化速度は、Qh×Cin - Qh×Cout - CLint×fu×Coutと表される。
論点とアプローチ:
この式は、肝臓における薬物のマスバランスを表現しています。薬物の流入量、流出量、そして消失量を考慮しています。
解法:
肝臓内での薬物量の変化速度 dA/dt は以下のように表されます:
dA/dt = Qh × Cin - Qh × Cout - CLint × fu × Cout
Qh × Cin は肝臓に流入する薬物量。
Qh × Cout は肝臓から流出する薬物量。
CLint × fu × Cout は肝臓内で消失する薬物量。
この式は、薬物の肝臓内でのマスバランスを正確に反映しており、選択肢4は正しいです。
エビデンス:
肝臓における薬物動態の基本原理は、Pang and Rowland (1977) の論文で詳述されています。
Ref.
Pang, K. S., & Rowland, M. (1977). Hepatic clearance of drugs. I. Theoretical considerations of a "well-stirred" model and a "parallel tube" model. Influence of hepatic blood flow, plasma and blood cell binding, and the hepatocellular enzymatic activity on hepatic drug clearance. Journal of Pharmacokinetics and Biopharmaceutics, 5(6), 625-653.
選択肢5: 定常状態におけるCLintはQhにほぼ等しい。
論点とアプローチ:
この記述は、特定の条件下で成立しますが、一般的な特性ではありません。高抽出比薬物の場合、定常状態での薬物消失が肝血流量(Qh)に依存することが多いため、このような状況が考えられます。
解法:
高抽出比薬物の場合、薬物の消失速度が肝血流量にほぼ等しくなることがあります:
CLint × fu × Cin ≒ Qh × Cin
CLint × fu が非常に大きい場合、薬物はほぼ全量が肝臓で代謝されます。その結果、流入する薬物の大部分が消失し、 Cout が非常に小さくなります。
これにより、定常状態では CLint ≒ Qh となりますが、これは高抽出比薬物に限られます。
しかし、一般的に、 CLint と Qh が等しいとは限りません。したがって、選択肢5は特定の条件下でのみ正しいため、一般的には正しくありません。
エビデンス:
薬物の肝臓での高抽出特性とその影響について、Wilkinson and Shand (1975) が詳しく論じています。
Ref.
Wilkinson, G. R., & Shand, D. G. (1975). A physiological approach to hepatic drug clearance. Clinical Pharmacology & Therapeutics, 18(4), 377-390.
以上で、論点整理を終わります。
理解できたでしょうか?
大丈夫です。
完全攻略を目指せ!
はじめましょう。
薬剤師国家試験の薬学理論問題【薬剤】からwell-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度を論点とした問題です。
なお、以下の解説は、著者(Yukiho Takizawa, PhD)がプロンプトを作成して、その対話に応答する形でGPT4o & Copilot 、Gemini 1.5 Pro、またはGrok 2 (beta) が出力した文章であって、著者がすべての出力を校閲しています。
生成AIの製造元がはっきりと宣言しているように、生成AIは、その自然言語能力および取得している情報の現在の限界やプラットフォーム上のインターフェースのレイト制限などに起因して、間違った文章を作成してしまう場合があります。
疑問点に関しては、必要に応じて、ご自身でご確認をするようにしてください。
松廼屋|論点解説 薬剤師国家試験対策ノート問107-176【薬剤】論点:well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度|matsunoya (note.com)
Here we go.
第107回薬剤師国家試験|薬学理論問題 /
問176
一般問題(薬学理論問題)【薬剤】
問107-176
Q. 図は、well-stirred modelに基づいた肝臓からの薬物消失モデルを示したものである。このモデルに関する記述のうち、正しいのはどれか。2つ選べ。ただし、CLintは肝固有クリアランス、fuは血中タンパク非結合形分率、Cinは肝臓に流入する部位における血中薬物濃度、Coutは肝臓から流出する部位における血中薬物濃度、Qhは肝血流量とする。図で肝臓は太枠で囲んだ部分。肝組織は、太枠で囲んだ部分の下半分。

■選択肢
1. 肝臓中の非結合形薬物濃度は不均一である。
2. 肝組織中の非結合形薬物濃度はCinに等しい。
3. 肝臓からの見かけの薬物消失速度は、CLint×fu×Coutと表される。
4. 肝臓における薬物量の変化速度は、Qh×Cin - Qh×Cout - CLint×fu×Coutと表される。
5. 定常状態におけるCLintはQhにほぼ等しい。
■■Grok 2 mini (beta)
薬剤|問 107-176
■論点|well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度
この問題の論点は、肝臓における薬物消失のメカニズムとその動態を正しく理解し、Well-stirred modelに基づく数式を使用して正しい薬物消失速度や濃度分布を導き出すことです。
■解説1|
肝臓からの見かけの薬物消失速度は、CLint×fu×Coutと表される。(選択肢3)[正しい]
この式は、肝臓内での薬物代謝速度を直接表しています。CLint(肝固有クリアランス)は薬物の代謝能力を、fu(非結合形分率)は薬物が非結合形で存在する割合を、Cout(流出濃度)は肝臓から流出する薬物濃度を示し、これらを掛けることで消失速度を求めます。

肝臓における薬物量の変化速度は、Qh×Cin - Qh×Cout - CLint×fu×Coutと表される。(選択肢4)[正しい]
この式は、薬物の肝臓内でのマスバランスを表しています。Qh×Cinは流入量、Qh×Coutは流出量、CLint×fu×Coutは消失量を表現し、それぞれの差が薬物の肝臓内での蓄積速度を示します。

■解説2|
選択肢3: Well-stirred modelでは、薬物の消失速度(v)は、肝臓から流出する薬物濃度(Cout)に基づいて計算されます。非結合形薬物のみが代謝に参加するため、fuはこの計算に必須です。また、CLintは薬物の代謝能力を反映し、Coutはその時点の薬物濃度を反映します。よって、この式は理論的に正確です。
選択肢4: 肝臓内での薬物の量変化速度は、薬物の流入、流出、そして消失を考慮した式で表されます。流入と流出の差分から消失量を引くことで、薬物の蓄積または減少速度が求められます。これは、薬物のマスバランスを直接反映しているため、正しい式です。
■結論|
選択肢3と4が正解です。
■補足|
肝臓中の非結合形薬物濃度は不均一である。(選択肢1)[誤り]
Well-stirred modelでは、肝臓内の薬物濃度が一様であると仮定しています。したがって、非結合形薬物濃度も一様であるべきです。
肝組織中の非結合形薬物濃度はCinに等しい。(選択肢2)[誤り]
肝臓に流入する薬物濃度(Cin)と肝組織内の非結合形薬物濃度は異なります。代謝や結合状態によって変化し、一様ではなく、Cinに等しいわけではありません。
定常状態におけるCLintはQhにほぼ等しい。(選択肢5)[誤り]
高抽出比薬物では条件によっては成立しますが、一般にはCLintとQhが等しいとは限りません。CLintは薬物の固有特性、Qhは生理的条件により異なります。
■Lecture
論点解説 Well-stirred Model 概説
目次
Well-stirred Modelの概要
薬物消失速度の計算
肝臓内での薬物濃度分布
定常状態と抽出比
選択肢の評価
まとめと結論
1. Well-stirred Modelの概要
モデルの基本概念:
Well-stirred modelは、肝臓が一つの均一な区画として扱われる薬物動態モデルです。このモデルでは、肝臓に入った薬物が即座に一様に混合され、分布することが仮定されます。
仮定と適用範囲:
一様性: 肝臓内での薬物濃度が一様である。
即時混合: 薬物が肝臓に入った瞬間に全域に均等に分布する。
非結合形薬物: 薬物の代謝は、非結合形(未結合の状態)で行われる。
このモデルは、薬物の肝臓での消失を理解するために広く使用されますが、すべての薬物や状況に適用できるわけではありません。
2. 薬物消失速度の計算
消失速度の式:
薬物の消失速度(v)は、以下のような式で表されます:
v = CLint × fu × Cout
ここで、
CLint は肝固有クリアランス(薬物の代謝能力)。
fu は血中での非結合形分率。
Cout は肝臓から流出する薬物濃度。
非結合形薬物の重要性:
薬物の代謝は非結合形(自由な形)で行われるため、 fu が重要な役割を果たします。これは、薬物がどの程度血液中のタンパク質に結合しているかを示し、結合していない部分が実際に代謝に寄与します。
3. 肝臓内での薬物濃度分布
一様性の仮定:
Well-stirred modelでは、肝臓内の薬物濃度が一様であると仮定します。これにより、肝臓内のどの位置でも薬物濃度が同じであるというシンプルなモデルが構築されます。
肝臓内濃度と流入・流出濃度の関係:
流入濃度(Cin): 肝臓に流入する薬物の濃度。
流出濃度(Cout): 肝臓から流出する薬物の濃度。
肝臓内での薬物濃度は、流入濃度と消失速度のバランスで決まります。モデルでは、
Cout = Cin × Qh / (Qh + CLint × fu)
と表されます。

4. 定常状態と抽出比
高抽出比薬物の特性:
高抽出比薬物は、肝血流量(Qh)に非常に依存します。これらの薬物は、肝臓を通過する際に大部分が代謝されます。
定常状態の条件:
定常状態では、薬物の流入量と消失量が等しくなります。高抽出比薬物の場合、
CLint × fu × Cin ≒ Qh × Cin
となります。これは、定常状態での薬物消失が肝血流量にほぼ等しくなることを示します。
5. 選択肢の評価
各選択肢の論点と解法:
選択肢1: 肝臓中の非結合形薬物濃度は不均一である。
Well-stirred modelでは均一性が仮定されており、不均一であるという記述は正しくない。
選択肢2: 肝組織中の非結合形薬物濃度はCinに等しい。
非結合形濃度は代謝や結合状態によりCinに等しくないため、正しくない。
選択肢3: 肝臓からの見かけの薬物消失速度は、CLint×fu×Coutと表される。
この式は消失速度を正確に表しており、正しい。
選択肢4: 肝臓における薬物量の変化速度は、Qh×Cin-Qh×Cout-CLint×fu×Coutと表される。
マスバランスを表す正しい式であり、正しい。
選択肢5: 定常状態におけるCLintはQhにほぼ等しい。
高抽出比薬物に限っては正しいが、一般には正しくない。
6. まとめ
モデルの限界と応用可能性:
Well-stirred modelは、薬物の肝臓内での動態を簡単に理解するための便利なツールです。しかし、このモデルは一部の仮定に基づいており、すべての薬物や状況に適用できるわけではありません。実際の薬物動態は、個々の薬物の特性、肝血流量、結合状態など多くの要因によって複雑に影響を受けます。
したがって、Well-stirred modelを適用する際には、その限界を理解し、必要に応じて他のモデル(例えば、parallel tube model)や実験データと組み合わせることが重要です。
Ref.
以下の文献は、Well-stirred modelと関連する薬物動態の理論についての詳細な情報を提供します。
Pang, K. S., & Rowland, M. (1977). Hepatic clearance of drugs. I. Theoretical considerations of a "well-stirred" model and a "parallel tube" model. Influence of hepatic blood flow, plasma and blood cell binding, and the hepatocellular enzymatic activity on hepatic drug clearance. Journal of Pharmacokinetics and Biopharmaceutics, 5(6), 625-653.
Wilkinson, G. R., & Shand, D. G. (1975). A physiological approach to hepatic drug clearance. Clinical Pharmacology & Therapeutics, 18(4), 377-390.
Rowland, M., & Tozer, T. N. (2011). Clinical Pharmacokinetics and Pharmacodynamics: Concepts and Applications (4th ed.). Philadelphia: Lippincott Williams & Wilkins.
以上の文献は、薬物動態学における基本的な理論と応用について包括的にカバーしています。
必須問題の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 必須問題 第106回-第109回 一覧 powered by Gemini 1.5 Pro, Google AI Studio & GPT4, Copilot|matsunoya (note.com)
薬学理論問題【薬剤】(1) の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 薬学理論問題 薬剤(1) 第106回-第109回 31問 powered by GPT4o, Chat GPT|matsunoya (note.com)
お疲れ様でした。
🍰☕🍊
では、問題を解いてみましょう!
すっきり、はっきりわかったら、合格です。
第107回薬剤師国家試験|薬学理論問題 /
問176
一般問題(薬学理論問題)【薬剤】
問107-176
Q. 図は、well-stirred modelに基づいた肝臓からの薬物消失モデルを示したものである。このモデルに関する記述のうち、正しいのはどれか。2つ選べ。ただし、CLintは肝固有クリアランス、fuは血中タンパク非結合形分率、Cinは肝臓に流入する部位における血中薬物濃度、Coutは肝臓から流出する部位における血中薬物濃度、Qhは肝血流量とする。図で肝臓は太枠で囲んだ部分。肝組織は、太枠で囲んだ部分の下半分。

■選択肢
1. 肝臓中の非結合形薬物濃度は不均一である。
2. 肝組織中の非結合形薬物濃度はCinに等しい。
3. 肝臓からの見かけの薬物消失速度は、CLint×fu×Coutと表される。
4. 肝臓における薬物量の変化速度は、Qh×Cin - Qh×Cout - CLint×fu×Coutと表される。
5. 定常状態におけるCLintはQhにほぼ等しい。
楽しく!驚くほど効率的に。
https://note.com/matsunoya_note
お疲れ様でした。
🍰☕🍊
またのご利用をお待ちしております。
ご意見ご感想などお寄せくださると励みになりうれしいです。
note からのサポート、感謝します。
今日はこの辺で、
それではまた
お会いしましょう。
Your best friend
Mats & BLNt
このコンテンツ
松廼屋|論点解説 薬剤師国家試験対策ノート問107-176【薬剤】論点:well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度|matsunoya (note.com)
Here; https://note.com/matsunoya_note/n/n61aa49700eaf
よろしければこちらもどうぞ
このコンテンツの制作者|
滝沢幸穂(Yukiho.Takizawa)phD
■Facebook プロフィール
https://www.facebook.com/Yukiho.Takizawa
■X (Former Twitter) プロフィール 🔒
https://twitter.com/YukihoTakizawa
CONTACT|
mail: info_01.matsunoya@vesta.ocn.ne.jp (Matsunoya Client Support)
tel: 029-872-9676
日々の更新情報など、Twitter @Mats_blnt_pharm から発信しています!
🔒 🐤💕 https://twitter.com/Mats_blnt_pharm
https://note.com/matsunoya_note
note.com 右上の🔍で
( matsunoya_note 🔍 )
松廼屋 Mats.theBASE
https://matsunoya.thebase.in/
サポート感謝します👍
最後までお読みいただきましてありがとうございました。
Here; https://note.com/matsunoya_note/n/n61aa49700eaf
松廼屋|論点解説 薬剤師国家試験対策ノート問107-176【薬剤】論点:well-stirred model / 肝臓 / 非結合形薬物濃度 / 見かけの薬物消失速度 / 薬物量の変化速度|matsunoya (note.com)
ここから先は
¥ 1,000
医療、健康分野のリカレント教育における「最強コンテンツ」を note で誰でもいつでも学習できる、 https://note.com/matsunoya_note はそんな場にしたい。あなたのサポートがあれば、それは可能です。サポート感謝します!松廼屋 matsunoya
