
松廼屋|論点解説 薬剤師国家試験対策ノート問106-179【薬剤】論点:ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値
第106回薬剤師国家試験|薬学理論問題 /
問179
一般問題(薬学理論問題)【薬剤】
問106-179
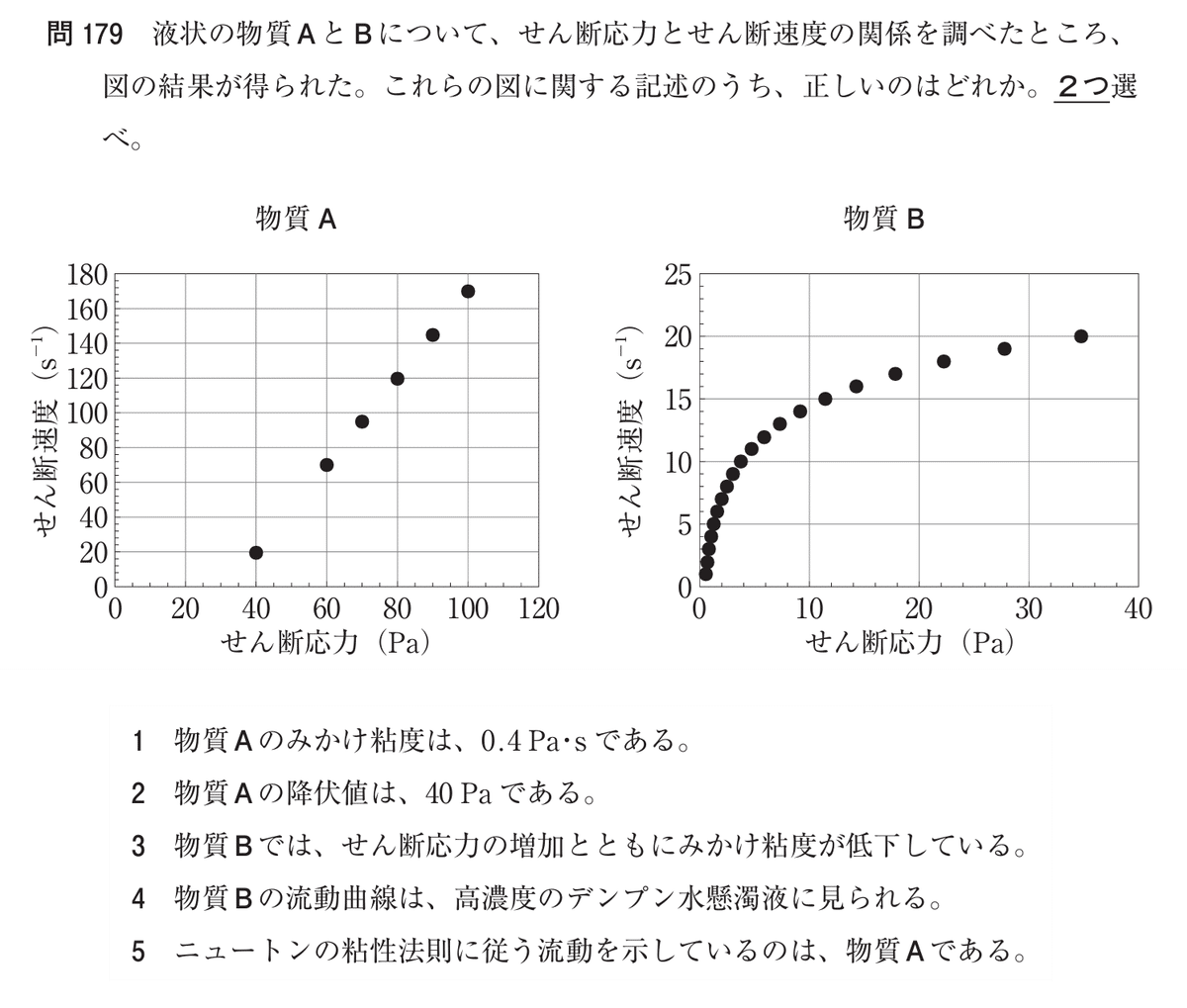
Q. 液状の物質AとBについて、せん断応力とせん断速度の関係を調べたところ、図の結果が得られた。これらの図に関する記述のうち、正しいのはどれか。2つ選べ。

■選択肢
1. 物質Aのみかけ粘度は、0.4Pa・sである。
2. 物質Aの降伏値は、40Paである。
3. 物質Bでは、せん断応力の増加とともにみかけ粘度が低下している。
4. 物質Bの流動曲線は、高濃度のデンプン水懸濁液に見られる。
5. ニュートンの粘性法則に従う流動を示しているのは、物質Aである。
こんにちは!薬学生の皆さん。
Mats & BLNtです。
matsunoya_note から、薬剤師国家試験の論点解説をお届けします。
苦手意識がある人も、この機会に、薬学理論問題【薬剤】を一緒に完全攻略しよう!
今回は、第106回薬剤師国家試験|薬学理論問題 / 問179、論点:ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値を徹底解説します。
薬剤師国家試験対策ノート NOTE ver.
matsunoya_note|note https://note.com/matsunoya_note
Here; https://note.com/matsunoya_note/n/n5f45a74caff8
松廼屋|論点解説 薬剤師国家試験対策ノート問106-179【薬剤】論点:ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値
薬剤師国家試験対策には、松廼屋の eラーニング
「薬剤師国家試験対策ノート」
マガジン|薬剤師国家試験対策ノート on note
👉マガジンをお気に入りに登録しよう!
このコンテンツの制作者|
滝沢 幸穂 Yukiho Takizawa, PhD
https://www.facebook.com/Yukiho.Takizawa
お友達や知り合いに、matsunota_note で学習したeラーニングを勧めてみたい方は、いいね!、口コミ、おススメなど、よろしくお願いします!
設問へのアプローチ|
第106回薬剤師国家試験の問179(問106-179)では、ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値に関する知識を問われました。テクニカルタームの定義と式がわかっていれば解ける計算問題が盛り込まれた問題です。

出題範囲:
製剤化のサイエンス|製剤の性質|半固形・液状材料|
流動と変形(レオロジー)について説明できる。👈ココ
高分子の構造と高分子溶液の性質(粘度等)について説明できる。👈ココ
薬剤師国家試験 出題基準
出典: 薬剤師国家試験のページ |厚生労働省 (mhlw.go.jp)
出題基準 000573951.pdf (mhlw.go.jp)
今回の解説は、ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値を語らせたら、ちょっと間違っちゃったり💦、ややまわりくどかったりする GPT4o と、ニュートン流体・非ニュートン流体って何?という状態なので、頼りないながら GPT4oと対話して、細かいPrompt修正と校正を加えたワタシのコラボです(^^)/
GPT4oとは、しばらく付き合っているのでわかってきたのですが、実は、プラスとマイナス、増加するのか減少するのか、上昇するのか低下するのかを絶対的な推論で判断できません。
どっちなのかは、単純な自然言語学習量のマスでなんとなく言っているのでロジックはないと思って良いです。少し長めに語らせると全く反対のことを言ったりします。長めだと定型化された文章のブロックが多いのでフィックスできる確率が上がるのですね。
上昇するのか低下するのかの判断に関しては、長めに語らせるのが間違わないコツです。
もう少し結論から言うと、プラスかマイナスかは、GPT4oに頼らず自分でじっくり考えて判断しましょう。
でも、まあ、今回はがんばってくれたので、選択肢3以外はそれほど大きな修正はする必要はなかったです。立派です。😭
基本の型を覚えるのは大事なので、時間があったらじっくり考えながら最後まで読んでください。
基本的な知識について復習しておきましょう。
■■GPT4o
この問題に出てくるテクニカルタームの定義を覚えよう
1. せん断応力(Shear Stress)
定義: 単位面積あたりに作用する力(せん断力)を指し、流体内で層が互いに滑るときに発生する力。
単位: パスカル(Pa)
式:
τ = F / A
ここで、τ はせん断応力、F はせん断力、A はせん断が発生する面積。
役割: せん断速度と粘度に依存して変化し、流体の挙動を制御する重要なパラメータ。
2. せん断速度(Shear Rate)
定義: 流体内の層がどの程度速く互いに移動するかを示す速度勾配。流動する層の間の速度差を距離で割ったもの。
単位: s^-1(1/秒)
式:
【γ・】 =Δ v /Δ y
ここで、【γ・】 はせん断速度、Δ v は速度差、Δ y は流体層間の距離。
役割: 流体がどの程度速く流れるかを表し、せん断応力に影響を与える。
3. 粘度(Viscosity)
定義: 流体の内部摩擦を示す量で、流体の「流れにくさ」を表す。流体が変形する速度(せん断速度)に対する抵抗。
単位: パスカル秒(Pa・s)
式(ニュートン流体の場合):
η = τ / 【γ・】
ここで、η は粘度、τ はせん断応力、【γ・】 はせん断速度。
種類: 見かけ粘度(非ニュートン流体での粘度)も含め、流体の種類に応じて定数かどうかが異なる。
4. ニュートン流体(Newtonian Fluid)
定義: せん断応力とせん断速度の間に線形関係があり、粘度が一定の流体。温度や圧力が一定であれば、せん断速度が変わっても粘度が変化しない。
特徴: 原点を通る直線的なグラフ(せん断応力 vs. せん断速度)を示す。
例: 水、空気、エタノールなど。
5. 非ニュートン流体(Non-Newtonian Fluid)
定義: せん断応力とせん断速度の間に線形関係がない流体。せん断速度に応じて粘度が変化する。
特徴: グラフは直線ではなく、さまざまな形状を示す。代表的な非ニュートン流体は、せん断減粘性、ダイラタント性、ビンガム流体などがある。
例: 高濃度デンプン水懸濁液、歯磨き粉、血液。
6. 降伏値(Yield Stress)
定義: ある流体が流動を開始するために必要な最小のせん断応力。降伏値を超えるまでは流体は変形しない。
単位: パスカル(Pa)
特徴: ビンガム流体や一部の非ニュートン流体で観察される。降伏値を持つ流体は、最小限の応力が必要で、それ以下では固体のように振る舞う。
7. ビンガム流体(Bingham Fluid)
定義: 降伏値を持つ非ニュートン流体。降伏値以上のせん断応力がかかると、流体はニュートン流体のように流れる。
式:
τ = τ_0 + η 【γ・】
ここで、τ_0 は降伏値、η は粘度、【γ・】 はせん断速度。
特徴: グラフでは、一定のせん断応力までは流動が起こらず、それを超えると線形関係が現れる。
例: 歯磨き粉、マヨネーズ。

8. せん断減粘性(Shear-Thinning Fluid)
定義: せん断速度が増加すると粘度が減少する非ニュートン流体。
特徴: せん断応力が増加するにつれて、流体が薄くなるような流動挙動を示す。
例: ペイント、ケチャップ、血液。
9. ダイラタント性(Shear-Thickening Fluid)
定義: せん断速度が増加すると粘度が増加する非ニュートン流体。ある速度以上で突然硬くなることが特徴。
特徴: 流体がせん断応力に反応してより粘り強くなるため、せん断速度に応じて硬化する。
例: 高濃度のデンプン懸濁液、砂糖水のスラリー。

まとめ
この問題では、物質AとBの流動特性を理解するために、せん断応力とせん断速度の関係、およびそれに伴う粘度の変化を解釈することが求められます。物質Aがビンガム流体、物質Bが非ニュートン流体の典型的な特性を示すため、各特性に基づいて適切な選択肢を選ぶことがポイントとなります。

論点を整理します。
■■GPT4o
総合的な論点
この問題の中心的な論点は、物質Aと物質Bのせん断応力とせん断速度の関係を解析し、粘性流体の特性を評価することです。
具体的には、これらの物質がどのような流動特性(ニュートン流体、非ニュートン流体、降伏値など)を持っているかを明らかにし、流体力学的な性質を評価することが求められます。
流動特性に関連する基本的な数式は、ニュートンの粘性法則に基づいて以下のように表されます。
τ = η ・ 【γ・】
τ:せん断応力 (Pa)
η:粘度 (Pa・s)
【γ・】:せん断速度 (s^-1)
ニュートン流体の場合、せん断応力とせん断速度は比例関係にあり、グラフは原点を通る直線になります。
一方、非ニュートン流体の場合、これらの関係は直線的でないか、降伏値が存在することが多く、グラフの形状が変化します。
物質Aのデータからは直線的な関係が見られ、せん断速度が0のときもある一定のせん断応力(降伏値)が存在します。これは、物質Aがビンガム流体に該当する可能性を示唆しています。
ビンガム流体の特徴として、一定のせん断応力(降伏値)を超えない限り、流動しません。

一方、物質Bのデータでは、初期段階ではせん断応力の増加に伴いせん断速度が増加しますが、やがて飽和する挙動が見られます。
この挙動は典型的な非ニュートン流体であり、粘度がせん断速度に依存することを示しています。
物質Bはダイラタント性または剪断減粘性(せん断応力の増加で粘度が変化する現象)を示している可能性があります。
次に、物質AとBのせん断応力とせん断速度の関係を分析し、それぞれの流動特性を詳しく解析します。
各選択肢の論点および解法へのアプローチ方法
選択肢1: 物質Aのみかけ粘度は、0.4Pa・sである。
見かけ粘度は、ニュートン流体におけるせん断応力とせん断速度の比率として定義されます。物質Aの場合、データポイント(せん断応力40Pa、80Pa)から直線の傾きを計算し、見かけ粘度を求めることが可能です。ビンガム流体の場合、見かけ粘度はこの傾きに該当します。

選択肢2: 物質Aの降伏値は、40Paである。
降伏値とは、流体が流動を開始するために必要な最小のせん断応力のことです。
物質Aの場合、せん断応力とせん断速度の関係が直線的であることから、降伏値が存在することが示唆されます。
この降伏値は、グラフがせん断速度0のときに交わるせん断応力の値として定義され、ここでは外挿により40Paが降伏値として考えられています。

選択肢3: 物質Bでは、せん断応力の増加とともにみかけ粘度が低下している。
物質Bのデータでは、せん断応力が一定以上になると、せん断速度の変化が飽和していることがわかります。これはせん断応力の増加に伴い見かけ粘度が増加することを示唆します。
この現象は、非ニュートン流体の一部のダイラタント性を示す流体に見られる特徴です。

選択肢4: 物質Bの流動曲線は、高濃度のデンプン水懸濁液に見られる。
高濃度デンプン懸濁液は一般的に非ニュートン流体であり、ダイラタント性や剪断減粘性を示すことが知られています。
物質Bの流動特性は、初期段階でせん断速度が上昇し、その後飽和するという挙動を示しており、このような特徴は高濃度デンプン懸濁液に似ています。

選択肢5: ニュートンの粘性法則に従う流動を示しているのは、物質Aである。
ニュートン流体は、せん断応力とせん断速度が線形かつ原点を通る直線的な関係を示します。
しかし、物質Aの場合、せん断速度が0のときにもせん断応力が存在するため、ニュートン流体ではなくビンガム流体の特性に近いと考えられます。

選択肢の論点および解法へのアプローチ方法を深掘り
選択肢1: 物質Aのみかけ粘度は、0.4Pa・sである。
物質Aのせん断応力とせん断速度の関係から、見かけ粘度を求めるには、ニュートンの粘性法則に基づいて、せん断応力とせん断速度の比率を計算します。
ただし、物質Aはビンガム流体の特徴を示しているため、粘度計算時には降伏値を考慮する必要があります。
ビンガム流体では、せん断応力 τ とせん断速度 【γ・】 の関係式は以下のように表されます:
τ = τ_0 + η 【γ・】
ここで、
τ_0:降伏値(流動を開始するための最小のせん断応力)
η:見かけ粘度
この場合、直線の傾き(見かけ粘度)をデータから計算するためには、2つのデータポイントを用いて計算します。
せん断応力 τ とせん断速度 【γ・】 の2つのポイント、(40 Pa, 20 s^-1)および(80 Pa, 120 s^-1)を使用します。

傾き η は次のように計算できます:
η =Δ τ /Δ 【γ・】 = (80 – 40) / (120 – 20)
= 40 / 100
= 0.4 Pa・s
したがって、見かけ粘度は0.4Pa・sとなります。
選択肢1は、物質Aの見かけ粘度が0.4Pa・sであることを示しており、この計算から正しいことが確認できます。
選択肢2: 物質Aの降伏値は、40Paである。
物質Aがビンガム流体であると仮定すると、降伏値 τ_0 は、流体がせん断速度0のときに流動を開始するために必要な最小のせん断応力を意味します。
ビンガム流体の場合、せん断応力とせん断速度の関係は次の式で表されます:
τ = τ_0 + η 【γ・】
この式で、τ_0(降伏値)を求めるには、データポイントから直線の切片を外挿する必要があります。物質Aのデータポイント(40Pa, 20s^-1)と(80Pa, 120s^-1)から、せん断応力とせん断速度の関係が直線的であることがわかります。
まず、2点間の直線の方程式を導出するために、直線の傾き(見かけ粘度)を計算します。
η = (80 – 40) / (120 – 20) = 40 / 100 = 0.4 Pa・s
次に、この傾きを使って直線の方程式を作ります。
τ = 0.4 ・ 【γ・】 + τ_0
データポイントの1つ(40Pa, 20s^-1)を代入して、τ_0を計算します。
40 = 0.4 ・ 20 + τ_0
40 = 8 + τ_0
τ_0 = 40 - 8 = 32 Pa

選択肢3: 物質Bでは、せん断応力の増加とともにみかけ粘度が低下している。
物質Bのせん断応力とせん断速度の関係を見ると、非ニュートン流体の典型的な挙動を示していることがわかります。
データから、せん断応力が増加すると最初はせん断速度が上昇しますが、せん断応力が高くなるとせん断速度の増加が鈍化し、飽和に近い挙動を見せています。

このような飽和現象は、流体内部の分子や粒子の相互作用が強くなることによって説明されます。
物質Bのような流体では、せん断応力が一定のしきい値を超えると、内部の構造が「最大の流れ」を形成し、それ以上せん断応力をかけても新たな流動が生じない状態に達します。
この結果、見かけ粘度が一定になるか、さらには上昇することがあります。
せん断減粘性を定量的に評価するために、見かけ粘度は次のように定義されます:
η_app = τ / 【γ・】
ここで、物質Bのデータを使って、せん断応力とせん断速度に基づく見かけ粘度を計算します。
せん断応力4Pa、せん断速度10s^-1:
η_app = 4 / 10 = 0.4 Pa・sせん断応力35Pa、せん断速度20s^-1:
η_app = 35 / 20 = 1.75 Pa・s
見かけ粘度は、せん断応力とせん断速度の比率であるため、せん断速度が急激に増加している領域では見かけ粘度が低くなる傾向があります。
しかし、物質Bのように、せん断速度の増加が鈍化し飽和状態に達すると、見かけ粘度はほぼ一定、または上昇する可能性があります。
このような挙動は、プラスチック流体や擬塑性流体に見られることが多いです。
物質Bの場合、せん断速度の増加が飽和していることから、見かけ粘度は一定になるか、さらには増加する可能性があります。したがって、「せん断応力の増加とともに見かけ粘度が低下している」という選択肢は明確に誤りであり、逆にせん断応力が増加すると見かけ粘度は低下せず、一定もしくは上昇する挙動を示すと考えられます。
このことから、選択肢3は誤りであると判断できます。
選択肢4: 物質Bの流動曲線は、高濃度のデンプン水懸濁液に見られる。
高濃度のデンプン水懸濁液は、一般的に非ニュートン流体であり、特にダイラタント性や剪断減粘性といった特徴を示します。これらの特徴は、せん断応力が一定以上に増加すると流動特性が変化し、見かけ粘度が変動する挙動として現れます。
物質Bのデータを見ると、初期段階ではせん断応力の増加に伴いせん断速度も上昇していますが、せん断応力が高くなるとせん断速度の増加が鈍化し、飽和するような挙動が見られます。この特徴は、せん断速度に対するせん断応力の非線形な関係を示しており、典型的な非ニュートン流体の特性に当てはまります。

高濃度のデンプン水懸濁液は、特にダイラタント性(せん断応力が増加すると見かけ粘度が増加する現象)を示す場合があります。ダイラタント性流体では、ある臨界せん断速度を超えると、粒子間の相互作用が強まり、流体全体が硬化するような挙動が見られることがあります。これは物質Bのデータにおける「せん断応力の増加とせん断速度の飽和」という現象に類似しています。
したがって、物質Bの流動曲線が高濃度のデンプン水懸濁液の挙動と類似しているという記述は、科学的に正しい可能性が高いと考えられます。この流動特性は非ニュートン流体に典型的であり、選択肢4は正しい可能性があります。
選択肢5: ニュートンの粘性法則に従う流動を示しているのは、物質Aである。
ニュートン流体は、せん断応力 τ がせん断速度 【γ・】 に比例し、次の式で表されます。
τ = η 【γ・】
この関係では、せん断応力とせん断速度が原点を通る直線的な関係を持ち、粘度 η は定数となります。ニュートン流体は、せん断速度が変わっても粘度が一定であるという特徴を持ちます。
物質Aのデータを見てみると、せん断応力とせん断速度の関係は線形であるものの、せん断速度が0のときにもせん断応力が存在するため、原点を通っていません。これは、物質Aがビンガム流体の特徴を示していることを示唆します。ビンガム流体は、一定の降伏値 τ_0 を超えないと流動しない性質を持ち、せん断応力とせん断速度の関係は次の式で表されます。
τ = τ_0 + η 【γ・】
したがって、物質Aは降伏値を持つ流体であり、ニュートン流体ではなくビンガム流体に該当します。ニュートン流体のように原点を通る直線的な関係を示すわけではないため、この選択肢は誤りです。

ニュートン流体の特性を持つ流体が存在する場合は、せん断応力がせん断速度に比例し、見かけ粘度が一定である必要があります。しかし、物質Aはこの特徴に当てはまりません。
このため、選択肢5は誤りであると結論づけられます。
8: 引用文献のリスト
Barnes, H. A. (2000). A Handbook of Elementary Rheology. Institute of Non-Newtonian Fluid Mechanics.
この文献では、ニュートン流体および非ニュートン流体(ビンガム流体、せん断減粘性流体など)の基礎的な流動挙動について詳細に解説されており、物質Aおよび物質Bの挙動の科学的根拠を提供しています。Chhabra, R. P., & Richardson, J. F. (2008). Non-Newtonian Flow and Applied Rheology: Engineering Applications. Butterworth-Heinemann.
ビンガム流体の特性や非ニュートン流体のせん断減粘性についての説明が含まれており、物質Aと物質Bの振る舞いを理解するために参考としました。Steffe, J. F. (1996). Rheological Methods in Food Process Engineering. Freeman Press.
食品における高濃度懸濁液(デンプン水懸濁液など)の流動特性に関する記述があり、物質Bの挙動と比較するために使用しました。
以上で、論点整理を終わります。
理解できたでしょうか?
大丈夫です。
完全攻略を目指せ!
はじめましょう。
薬剤師国家試験の薬学理論問題【薬剤】からニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値を論点とした問題です。
なお、以下の解説は、著者(Yukiho Takizawa, PhD)がプロンプトを作成して、その対話に応答する形でGPT4o & Copilot 、Gemini 1.5 Pro、またはGrok 2 (beta) が出力した文章であって、著者がすべての出力を校閲しています。
生成AIの製造元がはっきりと宣言しているように、生成AIは、その自然言語能力および取得している情報の現在の限界やプラットフォーム上のインターフェースのレイト制限などに起因して、間違った文章を作成してしまう場合があります。
疑問点に関しては、必要に応じて、ご自身でご確認をするようにしてください。
松廼屋|論点解説 薬剤師国家試験対策ノート問106-179【薬剤】論点:ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値|matsunoya
Here we go.
第106回薬剤師国家試験|薬学理論問題 /
問179
一般問題(薬学理論問題)【薬剤】
問106-179
Q. 液状の物質AとBについて、せん断応力とせん断速度の関係を調べたところ、図の結果が得られた。これらの図に関する記述のうち、正しいのはどれか。2つ選べ。

■選択肢
1. 物質Aのみかけ粘度は、0.4Pa・sである。
2. 物質Aの降伏値は、40Paである。
3. 物質Bでは、せん断応力の増加とともにみかけ粘度が低下している。
4. 物質Bの流動曲線は、高濃度のデンプン水懸濁液に見られる。
5. ニュートンの粘性法則に従う流動を示しているのは、物質Aである。
■■GPT4o
薬剤|問 106-179
■論点|ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値
この問題の論点は、物質AとBの流動特性を正確に解釈し、見かけ粘度や流動曲線に基づく適切な選択肢を特定することです。
■解説1|
物質Aのみかけ粘度は、0.4 Pa・sである。(選択肢1) [正しい]
物質Aは、データポイント(40Pa, 20s^-1)と(80Pa, 120s^-1)から、せん断応力とせん断速度の直線的な関係が見られます。この関係に基づいて、見かけ粘度 η_app は次の式で計算できます。
η_app =Δ τ /Δ 【γ・】 = (80 – 40) / (120 – 20) = 0.4 Pa・s
この計算結果から、物質Aの見かけ粘度は0.4 Pa・sであることが確認できます。

物質Bの流動曲線は、高濃度のデンプン水懸濁液に見られる。(選択肢4) [正しい]
物質Bは、せん断応力の増加とともに最初はせん断速度が上昇しますが、せん断応力が高くなるとせん断速度が飽和します。これは、典型的な非ニュートン流体の挙動を示しています。
高濃度のデンプン水懸濁液など、非ニュートン流体はダイラタント性やせん断減粘性を示すことが多く、物質Bの流動曲線はこの挙動に類似しているため、正しい記述です。

■解説2|
物質Aは直線的なせん断応力とせん断速度の関係から、ビンガム流体の特性を示している可能性がありますが、見かけ粘度は一定です。
物質Bのような非ニュートン流体は、せん断応力が増加すると見かけ粘度が変動する特性を示します。高濃度デンプン懸濁液はせん断応力が増加すると、粘度が増加し流動特性が変化することが知られています。
■結論|
選択肢1(物質Aのみかけ粘度は、0.4Pa・sである)および選択肢4(物質Bの流動曲線は高濃度のデンプン水懸濁液に見られる)は正しいです。
物質Aはビンガム流体のような振る舞いをし、物質Bは非ニュートン流体の特徴を示しています。
■補足|
物質Aの降伏値は、40Paである。(選択肢2) [誤り]
物質Aの降伏値は40Paではなく、データから外挿すると約32Paです。降伏値は、ビンガム流体においては、流動を開始する最小のせん断応力を指します。

物質Bでは、せん断応力の増加とともに見かけ粘度が低下している。(選択肢3) [誤り]
物質Bは、せん断速度が増加するが飽和する挙動を示し、見かけ粘度が増加するため、この記述は誤りです。
このような飽和現象は、流体内部の分子や粒子の相互作用が強くなることによって説明されます。
物質Bのような流体では、せん断応力が一定のしきい値を超えると、内部の構造が「最大の流れ」を形成し、それ以上せん断応力をかけても新たな流動が生じない状態に達します。この結果、見かけ粘度が一定になるか、さらには上昇することがあります。

ニュートンの粘性法則に従う流動を示しているのは、物質Aである。(選択肢5) [誤り]
物質Aはニュートン流体ではなく、ビンガム流体の特性を持っているため、ニュートンの粘性法則には従いません。

■Lecture|
まとめ
下記のプロンプトを、GPT4o に入力すると、選択肢3の論点解説をまとめてくれます。お試しあれ(^^)/ (真偽は自分で確かめなさいー🤖)
今日のPrompts:
下記の選択肢3の解説に関して、画像を解析して、下記の画像の図の説明も参考にして、物質Bの見かけ粘度について論述してください。
物質Bでは、せん断応力の増加とともに見かけ粘度が低下している。(選択肢3) [誤り]
図の説明
物質B せん断応力(Pa)の増加に伴ってせん断速度(s^-1)は増加したが、やがて飽和がみられた。
せん断応力(Pa)|せん断速度(s^-1)
4|10
11|15
35|20

必須問題の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 必須問題 第106回-第109回 一覧 powered by Gemini 1.5 Pro, Google AI Studio & GPT4, Copilot|matsunoya (note.com)
薬学理論問題【薬剤】(1) の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 薬学理論問題 薬剤(1) 第106回-第109回 31問 powered by GPT4o, Chat GPT|matsunoya (note.com)
お疲れ様でした。
🍰☕🍊
では、問題を解いてみましょう!
すっきり、はっきりわかったら、合格です。
第106回薬剤師国家試験|薬学理論問題 /
問179
一般問題(薬学理論問題)【薬剤】
問106-179
Q. 液状の物質AとBについて、せん断応力とせん断速度の関係を調べたところ、図の結果が得られた。これらの図に関する記述のうち、正しいのはどれか。2つ選べ。

■選択肢
1. 物質Aのみかけ粘度は、0.4Pa・sである。
2. 物質Aの降伏値は、40Paである。
3. 物質Bでは、せん断応力の増加とともにみかけ粘度が低下している。
4. 物質Bの流動曲線は、高濃度のデンプン水懸濁液に見られる。
5. ニュートンの粘性法則に従う流動を示しているのは、物質Aである。
楽しく!驚くほど効率的に。
https://note.com/matsunoya_note
お疲れ様でした。
🍰☕🍊
またのご利用をお待ちしております。
ご意見ご感想などお寄せくださると励みになりうれしいです。
note からのサポート、感謝します。
今日はこの辺で、
それではまた
お会いしましょう。
Your best friend
Mats & BLNt
このコンテンツ
松廼屋|論点解説 薬剤師国家試験対策ノート問106-179【薬剤】論点:ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値|matsunoya
Here; https://note.com/matsunoya_note/n/n5f45a74caff8
よろしければこちらもどうぞ
このコンテンツの制作者|
滝沢幸穂(Yukiho.Takizawa)phD
■Facebook プロフィール
https://www.facebook.com/Yukiho.Takizawa
■X (Former Twitter) プロフィール 🔒
https://twitter.com/YukihoTakizawa
CONTACT|
mail: info_01.matsunoya@vesta.ocn.ne.jp (Matsunoya Client Support)
tel: 029-872-9676
日々の更新情報など、Twitter @Mats_blnt_pharm から発信しています!
🔒 🐤💕 https://twitter.com/Mats_blnt_pharm
https://note.com/matsunoya_note
note.com 右上の🔍で
( matsunoya_note 🔍 )
松廼屋 Mats.theBASE
https://matsunoya.thebase.in/
サポート感謝します👍
最後までお読みいただきましてありがとうございました。
Here; https://note.com/matsunoya_note/n/n5f45a74caff8
松廼屋|論点解説 薬剤師国家試験対策ノート問106-179【薬剤】論点:ニュートン流体・非ニュートン流体 / せん断応力・せん断速度・粘度・降伏値|matsunoya
ここから先は
¥ 1,000
Amazonギフトカード5,000円分が当たる
医療、健康分野のリカレント教育における「最強コンテンツ」を note で誰でもいつでも学習できる、 https://note.com/matsunoya_note はそんな場にしたい。あなたのサポートがあれば、それは可能です。サポート感謝します!松廼屋 matsunoya
