
松廼屋|論点解説 薬剤師国家試験対策ノート問106-174【薬剤】論点:線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態
第106回薬剤師国家試験|薬学理論問題 /
問174
一般問題(薬学理論問題)【薬剤】
問106-174
Q. 肝代謝のみで消失する薬物400mgをヒトに単回静脈内投与した際、図に示す血中濃度推移が得られた。この薬物の体内動態は線形性を示し、経口投与時に門脈血中に移行する割合は100%である。この薬物を反復経口投与し、定常状態での平均血中薬物濃度を3.5μg/mLとしたい。この薬物の肝クリアランス(L/h)及び1日あたりの投与量(mg)の組合せとして最も適切なのはどれか。1つ選べ。なお、肝血流速度は80L/h、ln2=0.693とする。

クリアランス(L/h)|1日あたりの投与量(mg)
■選択肢
1. 5|500
2. 5|950
3. 5|1100
4. 10|500
5. 10|950
こんにちは!薬学生の皆さん。
Mats & BLNtです。
matsunoya_note から、薬剤師国家試験の論点解説をお届けします。
苦手意識がある人も、この機会に、薬学理論問題【薬剤】を一緒に完全攻略しよう!
今回は、第106回薬剤師国家試験|薬学理論問題 / 問174、論点:線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態を徹底解説します。
薬剤師国家試験対策ノート NOTE ver.
matsunoya_note|note https://note.com/matsunoya_note
Here; https://note.com/matsunoya_note/n/n58141ac4e042
松廼屋|論点解説 薬剤師国家試験対策ノート問106-174【薬剤】論点:線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態
薬剤師国家試験対策には、松廼屋の eラーニング
「薬剤師国家試験対策ノート」
マガジン|薬剤師国家試験対策ノート on note
👉マガジンをお気に入りに登録しよう!
このコンテンツの制作者|
滝沢 幸穂 Yukiho Takizawa, PhD
https://www.facebook.com/Yukiho.Takizawa
お友達や知り合いに、matsunota_note で学習したeラーニングを勧めてみたい方は、いいね!、口コミ、おススメなど、よろしくお願いします!
設問へのアプローチ|

第106回薬剤師国家試験の問174(問106-174)では、線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態に関する知識を問われました。計算問題です。
計算問題は、慣れです。
手を動かして繰り返し解いてみてください。
2分30秒以内に解けるか、タイマーで時間を測定しながら解いてみると自信がつきます。
この問題は、グラフから数値を読み取って、その後、その数値を用いて計算を行う手順で進むところがひと手間増えています。
読み取った数値は、メモっておきましょう。
計算のコツは、最初に単位をそろえることです。血中濃度は、µg/mLからmg/Lに単位を変換しておくと計算が単純になります。
1 µg/mL = 1 mg/L
あと、何度も言っていますが、選択肢の有効数字を確認して、その有効数字に合わせた四則演算をすると早く正確な数値が出せます。

なお、上記のグラフは、1-コンパートメントモデルの基本の式を自然対数に変換した下記の式に基づいてプロットされたグラフです。



つまり、切片が ln(C_0)で、傾きが -k の、投与後時間(t)の関数をグラフに表しています。
2通りのアプローチがあります。
クリアランス CL の算出:
グラフから C_0 と C_t を読み取り k を求め、その後 V_d を用いて CL を求める解法。
または、t1/2 を読み取って k を求め、その後 V_d を用いて CL を求める解法。
どちらにしてもV_dを用いるので、最初にサクッと計算してメモっておくとよいです。
投与量 D の算出:
定常状態の平均血中濃度 C_ss を3.5 μg/mL(3.5 mg/L)に保つための投与量を、クリアランス CL と投与間隔 τ を用いて求める。
手を動かして、両方の算出プロセスを繰り返し練習しておくとよいです。
以下に、2つの解法を、Grok 2 mini (beta)にわかりやすく説明してもらったのでご覧ください。
■■Grok 2 mini (beta)
解法1. グラフから読み取ったC_0とC_tから算出する
初期濃度 C_0 と 時間 t 後の濃度 C_t から消失速度定数 k を求める:
C_t = C_0 ・ e^-kt
k = ln(C_0 / C_t) / t


分布容積 V_d を求める: V_d = D / C_0 ここで、D は投与量。

クリアランス CL を求める: CL = k ・ V_d
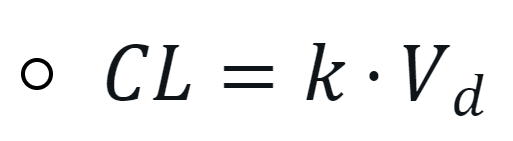
解法2. グラフから読み取った t1/2 から算出する
消失半減期 t1/2 をグラフから読み取る(この場合は3.5時間)。

消失速度定数 k を求める: k = ln(2) / t1/2

分布容積 V_d を求める: V_d = D / C_0

クリアランス CL を求める: CL = k ・ V_d

共通の工程
定常状態の血中濃度 C_ss を求める条件: C_ss = D / (CL ・ τ)
ここで、τ は投与間隔(ここでは24時間)。

目標 C_ss が与えられている場合、そのC_ss に達するための投与量 D を求める: D = C_ss ・ CL ・ τ

まとめ
クリアランス CL の算出:
グラフから C_0 と C_t を読み取り k を求め、その後 V_d を用いて CL を求める。
または、t1/2 を読み取って k を求め、その後 V_d を用いて CL を求める。
投与量 D の算出:
定常状態の平均血中濃度 C_ss を3.5 μg/mL(3.5 mg/L)に保つための投与量を、クリアランス CL と投与間隔 τ を用いて求める。
この問題の場合、初見で2分30秒以内に解けるのは、
Grok 2 mini (beta) くらいのものです。🤖
でも、ここで焦ってはいけません。
2分30秒以内に解くことができるまで、何回かチャレンジしてみてください。
この努力が、いつか、薬剤師になってからの糧になるに違いありません。
まず基本的な知識について復習しておきましょう。
■■Grok 2 mini (beta)
※一部、GPT4oで出力したLaTexの式の画像を使用しています。
※分布容積の表記が、VとV_dの場合がありますが同じ概念を示しています。
※アンダーバーは、原則、下付き文字を定義しています。
線形1-コンパートメントモデル
1: 消失速度定数 k


薬物の消失速度定数 k は、薬物が体内からどの速さで消えていくかを示します。この値は、時間の単位 (1/h) で表され、薬物がどのくらいの割合で減少するかを決定します。
2: 消失半減期 t1/2

消失半減期は、薬物の濃度が半分になるまでの時間です。
これは
t1/2 = ln 2 / k = 0.693 / k
の式で表されます。
消失半減期は、薬物の消失速度を理解する上で重要なパラメーターです。
3: クリアランス CL
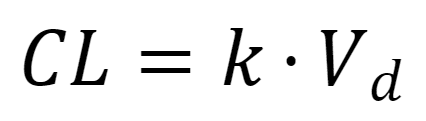
クリアランス CL は次のように求められます:
CL = k ・ V
4: 定常状態(反復投与)

ただし、バイオアベイラビリティ F=1
定常状態は、薬物の投与速度と消失速度が釣り合う状態です。この状態では、血中濃度は一定になります。
5: 分布容積 V

分布容積は、薬物が体内にどのくらい広がるかを示します。
初期投与量 D とその直後の血中濃度 C_0 がわかれば、分布容積 V は
V = D / C_0
という式で求められます。
6: 定常状態での血中濃度の計算

ただし、バイオアベイラビリティ F=1
定常状態での血中濃度 C_ss は、以下の式で表されます:
定常状態の血中濃度 C_ss を求める条件:
C_ss = D / (CL ・ τ)
ここで、τ は投与間隔(ここでは24時間)。
目標 C_ss が与えられている場合、そのC_ss に達するための投与量 D を求める:
D = C_ss ・ CL ・ τ
説明に沿って、何度か計算してみてください。
完全攻略を目指せ!
はじめましょう。
薬剤師国家試験の薬学理論問題【薬剤】から線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態を論点とした問題です。
なお、以下の解説は、著者(Yukiho Takizawa, PhD)がプロンプトを作成して、その対話に応答する形でGPT4o & Copilot 、Gemini 1.5 Pro、またはGrok 2 (beta) が出力した文章であって、著者がすべての出力を校閲しています。
生成AIの製造元がはっきりと宣言しているように、生成AIは、その自然言語能力および取得している情報の現在の限界やプラットフォーム上のインターフェースのレイト制限などに起因して、間違った文章を作成してしまう場合があります。
疑問点に関しては、必要に応じて、ご自身でご確認をするようにしてください。
松廼屋|論点解説 薬剤師国家試験対策ノート問106-174【薬剤】論点:線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態|matsunoya (note.com)
Here we go.
第106回薬剤師国家試験|薬学理論問題 /
問174
一般問題(薬学理論問題)【薬剤】
問106-174
Q. 肝代謝のみで消失する薬物400mgをヒトに単回静脈内投与した際、図に示す血中濃度推移が得られた。この薬物の体内動態は線形性を示し、経口投与時に門脈血中に移行する割合は100%である。この薬物を反復経口投与し、定常状態での平均血中薬物濃度を3.5μg/mLとしたい。この薬物の肝クリアランス(L/h)及び1日あたりの投与量(mg)の組合せとして最も適切なのはどれか。1つ選べ。なお、肝血流速度は80L/h、ln2=0.693とする。

クリアランス(L/h)|1日あたりの投与量(mg)
■選択肢
1. 5|500
2. 5|950
3. 5|1100
4. 10|500
5. 10|950
■■Grok 2 mini (beta)
薬剤|問 106-174
■論点|線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態
この問題は、薬物の消失特性(消失半減期やクリアランス)を把握することから始まります。
これは、投与された薬物がどれだけ速く体から排除されるかを理解するためのプロセスです。
次に、反復投与時に定常状態での血中濃度を管理するために必要な投与量を決定する必要があります。
定常状態での血中濃度は、薬物の有効性や安全性を確保するための重要な指標であり、これを特定の範囲内に保つことで治療効果を最大化します。
さらに、選択肢の中から最も適切なクリアランスと投与量の組み合わせを選定することで、実際の医療現場での投与計画の作成方法を学びます。
これは、理論的な計算が実際の治療にどのように反映されるべきかという臨床応用の観点からも重要です。
この一連のプロセスは、薬物動態学の基本的な理解と、それを活用した治療計画の立案能力を問うものです。
■解法1 グラフ(図)から読み取ったC_0とC_tから算出する
1: 消失速度定数 k の計算

まず消失速度定数 k を求めます。
C(t) = C_0 ・ e^(-kt)
初期濃度 C_0 = 8 μg/mL = 8 mg/L 、
7時間後の濃度 C_7 = 2 μg/mL = 2 mg/L です。
2 = 8 ・ e^(-7k)
2 / 8 = e^(-7k)
ln(2 / 8) = -7k
ln(1 / 4) = -7k
-2 ln(2) = -7k
k = 2 ln(2) / 7
2: クリアランスの計算
クリアランス CL は次のように求められます:
CL = k ・ V_d
ここで、V_d は、投与量と初期濃度から求めることができます。
V_d = 投与量 / C_0 = 400 mg / 8 mg/L = 50 L
CL = 2 (ln(2) / 7) ・ 50
CL = 2 ・ (0.693 / 7) ・ 50 = 1.386 / 7 ・ 50 ≒ 9.9 L/h
3: 1日あたりの投与量の計算
定常状態での平均血中濃度を C_ss とすると、投与量 D は次のように求められます:
C_ss = D / (CL・τ)
ここで、τ は投与間隔(24時間)、C_ss = 3.5 mg/L です。
3.5 = D / (9.9 ・ 24)
D = 3.5 × 9.9 × 24 ≒ 822.6 mg/day
しかし、選択肢ではクリアランスが10 L/h とされています。この情報に基づいて再計算します。
CL = 10 L/h
D = 3.5 × 10 × 24 = 840 mg/day
まとめ
クリアランス:10 L/h
1日あたりの投与量:840 mg
■解法2. グラフから読み取った t1/2 から算出する
情報に基づいて、薬物の消失半減期 (t1/2) を計算し、その後のクリアランスと投与量を求めます。
1: 消失半減期の計算
血中濃度が初期濃度の半分になる時間が3.5時間であるとすると、これが消失半減期 (t1/2) です。

t1/2 = 3.5 時間
2: 消失速度定数 k の計算
t1/2 = ln(2) / k
3.5 = 0.693 / k
k = 0.693 / 3.5 ≒ 0.198 h^-1
3: クリアランスの計算
クリアランス CL は次のように求められます:
CL = k ・ V_d
分布容積 V_d は、初期濃度 C_0 と投与量 D から求めます。
V_d = D / C_0
V_d = 400 mg / 8 mg/L = 50 L
したがって、クリアランス CL は:
CL = 0.198 h^-1 × 50 L = 9.9 L/h
4: 1日あたりの投与量の計算
定常状態での平均血中濃度 C_ss を3.5 mg/Lに保つための投与量 D は:
C_ss = D / (CL ・ τ)
ここで、τ は24時間、C_ss = 3.5 mg/L です。
3.5 = D / (9.9 ・ 24)
D = 3.5 × 9.9 × 24 = 822.6 mg/day
まとめ
クリアランス:9.9 L/h
1日あたりの投与量:822.6 mg
ただし、正答が提示されている場合、クリアランスが10 L/hとされています。これを考慮して、再計算すると:
D = 3.5 × 10 × 24 = 840 mg/day
■結果
クリアランス:10 L/h
1日あたりの投与量:840 mg
■補足
正答の選択肢5 のとおりに、1日あたりの投与量 D は950 mgで、投与間隔 τ は24時間、クリアランス CL が10 L/hである場合の平均血中濃度を計算し、グラフのデータからの算出値と比較します。
1: クリアランスの確認
前提として、クリアランス CL が10 L/hであるとします。
2: 投与量と投与間隔の定義
1日あたりの投与量 D は950 mgで、投与間隔 τ は24時間です。
3: 定常状態の平均血中濃度の計算
定常状態での平均血中濃度 C_ss は以下の式で求められます:
C_ss = D / (CL ・ τ)
ここで、D = 950 mg、CL = 10 L/h、τ = 24 hを代入します。
C_ss = 950 / (10 × 24) = 950 / 240 = 3.9583 mg/L
まとめ
1日あたり950 mgの薬物を投与した場合の定常状態での平均血中濃度は、およそ 4.0 mg/L となります。
注意点
ここでの計算は、完全な線形薬物動態を前提にしています。
目標の定常状態の血中濃度が3.5 μg/mLから4.0 μg/mLに変更された場合、定常状態の1日あたりのAUCの増加率を算出します。
1: AUCの計算
AUCは、定常状態の血中濃度(C_ss)と投与間隔(τ)から算出できます。
AUC = C_ss × τ
3.5 μg/mL(3.5 mg/L)の場合:
AUC_3.5 = 3.5 mg/L × 24 h = 84 mg ・ h/L
4.0 μg/mL(4.0 mg/L)の場合:
AUC_4.0 = 4.0 mg/L × 24 h = 96 mg ・ h/L
2: 増加率の計算
増加率を求めるために、以下の式を使います:
増加率 (%) = (AUC_4.0 - AUC_3.5) / AUC_3.5 × 100
増加率 = (( 96 - 84) / 84) × 100 = (12 / 84) × 100 = 0.142857 × 100
増加率 ≒ 14.3%
まとめ
目標の定常状態の血中濃度が3.5 μg/mLから4.0 μg/mLに変更された場合、定常状態の1日あたりのAUCは14.3%増加します。
■Lecture
■■Grok 2 mini (beta)
論点解説
薬物の消失半減期 (t1/2) を分布容積 (V) とクリアランス (CL) で表すプロセスを、1-コンパートメントモデルを仮定して証明する

1: 消失速度定数 k の定義
1-コンパートメントモデルでは、薬物の濃度 C(t) は次のように指数関数で表されます:
C(t) = C_0 ・ e^(-kt)
ここで、C_0 は初期濃度、k は消失速度定数です。
2: 消失半減期の定義
消失半減期 t1/2 は、薬物の濃度が半分になるまでの時間です。したがって:

この関係を先の指数関数に代入すると:

3: 消失速度定数 k の式から t1/2 を求める
上の式を解くために、まず C_0 を両辺から除きます:

次に、自然対数を取ります:

-ln(2) = -kt1/2

4: クリアランスと分布容積の関係を導入
クリアランス CL は、消失速度定数 k と分布容積 V の積で表されます:

従って、消失速度定数 k を CL と V で表すと:

5: 消失半減期の最終的な式に到達
先の t1/2 の式に k の新しい表現を代入します:

t1/2 = ln(2) ・ V / CL
まとめ
以上のにより、1-コンパートメントモデルにおいて、消失半減期 t1/2 をクリアランス CL と分布容積 V で表すことができます:

必須問題の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 必須問題 第106回-第109回 一覧 powered by Gemini 1.5 Pro, Google AI Studio & GPT4, Copilot|matsunoya (note.com)
薬学理論問題【薬剤】(1) の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 薬学理論問題 薬剤(1) 第106回-第109回 31問 powered by GPT4o, Chat GPT|matsunoya (note.com)
お疲れ様でした。
🍰☕🍊
では、問題を解いてみましょう!
すっきり、はっきりわかったら、合格です。
第106回薬剤師国家試験|薬学理論問題 /
問174
一般問題(薬学理論問題)【薬剤】
問106-174
Q. 肝代謝のみで消失する薬物400mgをヒトに単回静脈内投与した際、図に示す血中濃度推移が得られた。この薬物の体内動態は線形性を示し、経口投与時に門脈血中に移行する割合は100%である。この薬物を反復経口投与し、定常状態での平均血中薬物濃度を3.5μg/mLとしたい。この薬物の肝クリアランス(L/h)及び1日あたりの投与量(mg)の組合せとして最も適切なのはどれか。1つ選べ。なお、肝血流速度は80L/h、ln2=0.693とする。

クリアランス(L/h)|1日あたりの投与量(mg)
■選択肢
1. 5|500
2. 5|950
3. 5|1100
4. 10|500
5. 10|950
楽しく!驚くほど効率的に。
https://note.com/matsunoya_note
お疲れ様でした。
🍰☕🍊
またのご利用をお待ちしております。
ご意見ご感想などお寄せくださると励みになりうれしいです。
note からのサポート、感謝します。
今日はこの辺で、
それではまた
お会いしましょう。
Your best friend
Mats & BLNt
このコンテンツ
松廼屋|論点解説 薬剤師国家試験対策ノート問106-174【薬剤】論点:線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態|matsunoya (note.com)
Here; https://note.com/matsunoya_note/n/n58141ac4e042
よろしければこちらもどうぞ
このコンテンツの制作者|
滝沢幸穂(Yukiho.Takizawa)phD
■Facebook プロフィール
https://www.facebook.com/Yukiho.Takizawa
■X (Former Twitter) プロフィール 🔒
https://twitter.com/YukihoTakizawa
CONTACT|
mail: info_01.matsunoya@vesta.ocn.ne.jp (Matsunoya Client Support)
tel: 029-872-9676
日々の更新情報など、Twitter @Mats_blnt_pharm から発信しています!
🔒 🐤💕 https://twitter.com/Mats_blnt_pharm
https://note.com/matsunoya_note
note.com 右上の🔍で
( matsunoya_note 🔍 )
松廼屋 Mats.theBASE
https://matsunoya.thebase.in/
サポート感謝します👍
最後までお読みいただきましてありがとうございました。
Here; https://note.com/matsunoya_note/n/n58141ac4e042
松廼屋|論点解説 薬剤師国家試験対策ノート問106-174【薬剤】論点:線形1-コンパートメントモデル / 静脈内投与 / 反復投与 / 定常状態|matsunoya (note.com)
ここから先は
¥ 700
医療、健康分野のリカレント教育における「最強コンテンツ」を note で誰でもいつでも学習できる、 https://note.com/matsunoya_note はそんな場にしたい。あなたのサポートがあれば、それは可能です。サポート感謝します!松廼屋 matsunoya
