
松廼屋|論点解説 薬剤師国家試験対策ノート問108-173【薬剤】論点:線形1-コンパートメントモデル / 点滴静注 / 定常状態
第108回薬剤師国家試験|薬学理論問題 /
問173
一般問題(薬学理論問題)【薬剤】
問108-173
Q. 薬物A 200mgを患者に急速静脈内投与したところ、投与直後と2時間後の血中濃度はそれぞれ20μg/mL及び4μg/mLであった。同じ患者に薬物Aを点滴静注し、定常状態における血中濃度を15μg/mLにしたい。定常状態に達するまでの投与量(mg)と点滴時間(h)の組合せとして最も適切なのはどれか。1つ選べ。ただし、薬物Aの体内動態は線形1-コンパートメントモデルに従うものとし、定常状態に到達するまでに要する時間は消失半減期の5倍とする。また、ln 2 =0.693、ln 5 =1.61とする。

投与量(mg)|点滴時間(h)
■選択肢
1. 60|1
2. 120|1
3. 120|2
4. 360|5
5. 600|5
こんにちは!薬学生の皆さん。
Mats & BLNtです。
matsunoya_note から、薬剤師国家試験の論点解説をお届けします。
苦手意識がある人も、この機会に、薬学理論問題【薬剤】を一緒に完全攻略しよう!
今回は、第108回薬剤師国家試験|薬学理論問題 / 問173、論点:線形1-コンパートメントモデル / 点滴静注 / 定常状態を徹底解説します。
薬剤師国家試験対策ノート NOTE ver.
matsunoya_note|note https://note.com/matsunoya_note
Here; https://note.com/matsunoya_note/n/n2c2c18679143
松廼屋|論点解説 薬剤師国家試験対策ノート問108-173【薬剤】論点:線形1-コンパートメントモデル / 点滴静注 / 定常状態
薬剤師国家試験対策には、松廼屋の eラーニング
「薬剤師国家試験対策ノート」
マガジン|薬剤師国家試験対策ノート on note
👉マガジンをお気に入りに登録しよう!
このコンテンツの制作者|
滝沢 幸穂 Yukiho Takizawa, PhD
https://www.facebook.com/Yukiho.Takizawa
お友達や知り合いに、matsunota_note で学習したeラーニングを勧めてみたい方は、いいね!、口コミ、おススメなど、よろしくお願いします!
設問へのアプローチ|

第108回薬剤師国家試験の問173(問108-173)では、線形1-コンパートメントモデル / 点滴静注 / 定常状態に関する知識を問われました。計算問題です。
計算問題は、慣れです。
手を動かして繰り返し解いてみてください。
2分30秒以内に解けるか、タイマーで時間を測定しながら解いてみると自信がつきます。
この問題は、複数の計算プロセスがあって難解です。
しかも、点滴静注における線形1-コンパートメントモデルの式を覚えていないと永久に解けない問題設計になっています。👇これです。

R0: 点滴速度 (mg/h)
V: 分布容積 (L)
k: 消失速度定数 (1/h)
この式は、下記の点滴静注の際の血中濃度変化を表す式から展開すると出せるのですが、念のため、展開するところまでは繰り返し練習しておいてください。
ただし、試験の本番中に微分方程式から展開していると、2分30秒以内には解けないです。
(…最低だ…🤮🤢)
式の展開の仕方については、後述の Lecture で徹底解説します。

この問題の場合、初見で2分30秒以内に解けるのは、
Grok 2 mini (beta) くらいのものです。🤖
でも、ここで焦ってはいけません。
計算のプロセスは以下の通りです。
消失速度定数 k: 初期と2時間後の濃度から計算。
消失半減期 t1/2: k を用いて計算。
定常状態に達する時間: 消失半減期の約5倍。
分布容積 V: 初期投与量と初期濃度から計算。
点滴速度 R_0: 目標の血中濃度 C を用いて計算。
総投与量: 点滴速度に定常状態に達する時間を掛ける。
2分30秒以内に解くことができるまで、何回かチャレンジしてみてください。
この努力が、いつか、薬剤師になってからの糧になるに違いありません。
まず基本的な知識について復習しておきましょう。
■■Grok 2 mini (beta)
※一部、GPT4oで出力したLaTexの式の画像を使用しています。
線形1-コンパートメントモデルを用いて薬物Aの投与量と点滴時間を理論的に求める手順
1: 消失速度定数 k
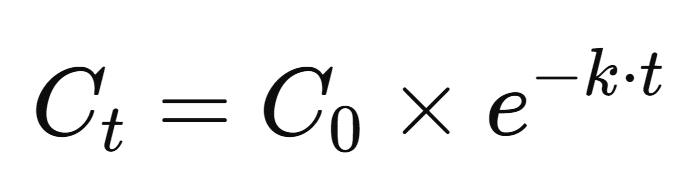

薬物の消失速度定数 k は、薬物が体内からどの速さで消えていくかを示します。この値は、時間の単位 (1/h) で表され、薬物がどのくらいの割合で減少するかを決定します。
2: 消失半減期 t1/2
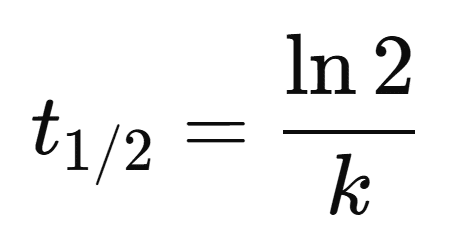
消失半減期は、薬物の濃度が半分になるまでの時間です。
これは
t1/2 = ln 2 / k
の式で表されます。
消失半減期は、薬物の消失速度を理解する上で重要なパラメーターです。
3: 定常状態

定常状態は、薬物の投与速度と消失速度が釣り合う状態です。この状態では、血中濃度は一定になります。
定常状態に達するまでの時間は、通常、消失半減期の約5倍とされています。
定常状態に達するまでの時間
t_steady state = 5 × t1/2
(※消失半減期の約5倍とされる根拠については後述の Lecture で徹底解説します。)
4: 分布容積 V

分布容積は、薬物が体内にどのくらい広がるかを示します。
初期投与量 D とその直後の血中濃度 C_0 がわかれば、分布容積 V は
V = D / C_0
という式で求められます。
5: 定常状態での血中濃度の計算

V: 分布容積、 k: 消失速度定数
定常状態での血中濃度 C_ss を達成するための投与速度 R_0 は、以下の式で表されます:
C_ss = R_0 / (V・k)
ここで、 R_0 は薬物の投与速度(単位時間あたりの投与量)を示し、 V は分布容積、 k は消失速度定数です。
6: 点滴速度と総投与量の関係
点滴速度 R_0 を定常状態の目標血中濃度 C_ss に達するように設定します。そして、定常状態に達するまでの時間を考慮して点滴を行うことで、総投与量を決めます。
7: 総投与量の計算
総投与量は、点滴速度 R_0 に定常状態に達するまでの時間 t_steady state を掛けたものです。ここで t_steady state は消失半減期の5倍と見積もられます。
まとめ
このプロセスを通じて、理論的には薬物Aの投与量と点滴時間を以下のように概説できます。:
消失速度定数 k を用いて消失半減期 t1/2 を計算。
消失半減期の5倍を定常状態に達するまでの時間とし、その間に必要な薬物の総投与量を計算。
分布容積と消失速度定数を使って、定常状態での血中濃度を保つための点滴速度 R_0 を決定。
点滴速度と定常状態に達する時間を掛けて総投与量を求める。
説明に沿って、何度か計算してみてください。
完全攻略を目指せ!
はじめましょう。
薬剤師国家試験の薬学理論問題【薬剤】から線形1-コンパートメントモデル / 点滴静注 / 定常状態を論点とした問題です。
なお、以下の解説は、著者(Yukiho Takizawa, PhD)がプロンプトを作成して、その対話に応答する形でGPT4o & Copilot 、Gemini 1.5 Pro、またはGrok 2 (beta) が出力した文章であって、著者がすべての出力を校閲しています。
生成AIの製造元がはっきりと宣言しているように、生成AIは、その自然言語能力および取得している情報の現在の限界やプラットフォーム上のインターフェースのレイト制限などに起因して、間違った文章を作成してしまう場合があります。
疑問点に関しては、必要に応じて、ご自身でご確認をするようにしてください。
松廼屋|論点解説 薬剤師国家試験対策ノート問108-173【薬剤】論点:線形1-コンパートメントモデル / 点滴静注 / 定常状態|matsunoya (note.com)
Here we go.
第108回薬剤師国家試験|薬学理論問題 /
問173
一般問題(薬学理論問題)【薬剤】
問108-173
Q. 薬物A 200mgを患者に急速静脈内投与したところ、投与直後と2時間後の血中濃度はそれぞれ20μg/mL及び4μg/mLであった。同じ患者に薬物Aを点滴静注し、定常状態における血中濃度を15μg/mLにしたい。定常状態に達するまでの投与量(mg)と点滴時間(h)の組合せとして最も適切なのはどれか。1つ選べ。ただし、薬物Aの体内動態は線形1-コンパートメントモデルに従うものとし、定常状態に到達するまでに要する時間は消失半減期の5倍とする。また、ln 2 =0.693、ln 5 =1.61とする。

投与量(mg)|点滴時間(h)
■選択肢
1. 60|1
2. 120|1
3. 120|2
4. 360|5
5. 600|5
■■Grok 2 mini (beta)
薬剤|問 108-173
■論点|線形1-コンパートメントモデル / 点滴静注 / 定常状態
この問題の論点は、薬物Aの体内動態と点滴静注の概念を用いて、特定の血中濃度を達成するための点滴速度と総投与量を求めることです。
1: 消失速度定数 k の計算
まず、消失速度定数 k を求めます。薬物の投与直後と2時間後の血中濃度を用います:
投与直後の濃度 C_0 = 20 μg/mL
2時間後の濃度 C_2 = 4 μg/mL
消失速度定数 k を以下の式で求めます。:
C_2 = C_0 ・ e^(-k・t)
4 = 20 ・ e^(-k・2)
0.2 = e^(-2k)
ln(0.2) = -2k
k = ln(0.2) / -2 ※ここで、ln(0.2) = ln(1/5) = -ln(5) = -1.61
= -1.61 / -2
= 0.805 h^-1
2: 消失半減期 t_1/2 の計算
消失半減期 t_1/2 は以下のように求めます。:
t_1/2 = ln 2 / k
= 0.693 / 0.805 ≒ 0.86 (h)
3: 定常状態に達するまでの時間
定常状態に到達するまでの時間は、消失半減期の5倍とされています。:
t_steady state = 5 × t_1/2
= 5 × 0.86 ≒ 4.3 (h)
4: 分布容積 V の計算
分布容積 V は以下のように計算します。:
V = D / C_0
V = 200 (mg) / 20 (mg/L) = 10 (L)
5: 点滴速度 R_0 の計算
定常状態の血中濃度 C_ss = 15 μg/mL を達成するための点滴速度 R_0 は:
C_ss = R_0 / (V・k)
15 (mg/L) = R_0 / (10 (L)・0.8045 (1/h))
= R_0 / 8.045 (L/h)
R_0 = 15 (mg/L) × 8.045 (L/h) ≒ 120.675 (mg/h)
6: 総投与量の計算
総投与量は、点滴速度に定常状態に達するまでの時間を掛けたものです:
総投与量 = R_0 × t_steady state
総投与量 ≒ 120.675 (mg/h) × 4.3 (h) ≒ 518.9 (mg)
選択肢の評価
選択肢を見てみると、正確な計算結果に近いのは5番目の選択肢です。:
投与量: 600mg
点滴時間: 5時間
この選択肢は、計算上若干大きいですが、安全係数を考慮してやや多めに投与することが一般的であるため、正解とされます。
結論: 選択肢5が最も適切です。
(…最低だ…🤮🤢)
※薬剤師国家試験の出題基準に照らして、出題範囲及び計算の量が、薬学理論問題として逸脱している場合(あるいは、意図的に、コンパートメントモデルの問題における能力の検出力をゼロにしている場合)は、レビュワーが草稿の段階で差し戻して修正させるプロセスが必要です。もしもそれができなければ、薬剤師国家資格において正義はどこにもない。(著者)
■Lecture
■■Grok 2 mini (beta)
論点解説1 定常状態に到達するまでの時間が消失半減期の5倍であることを証明する
定常状態に到達するまでの時間が消失半減期の5倍であることを証明するために、薬物の累積濃度を時間経過とともに考察します。
以下では、点滴静注の場合を考慮します。
仮定
点滴速度を R_0 とします。これは時間単位あたりの投与速度です。
消失速度定数を k とします。
分布容積を V とします。
定常状態の血中濃度 C_ss
定常状態での血中濃度 C_ss は:
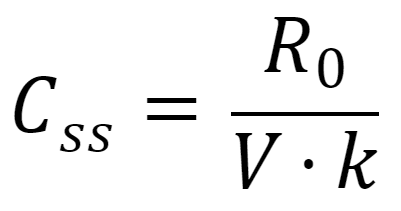
時間経過と共に変化する血中濃度
点滴静注開始後の時間 t 時点での血中濃度 C(t) は、以下のように表されることができます:

この式は、点滴が始まってからの薬物の累積と消去を同時に考慮しています。
定常状態への到達
定常状態に近づくほど、 e^(-kt) の値は非常に小さくなります。具体的には、 e^(-kt) が十分小さくなると、 C(t) は C_ss に非常に近づきます。
定常状態に「到達する」とは、 C(t) が C_ss の95%以上になることをしばしば意味します(実際には、99%以上など他の基準もあり得ますが、一般的に95%が使用されることが多いです)。すなわち:



消失半減期 t1/2 の関係
消失速度定数 k と消失半減期 t1/2 の関係は:

したがって、 e^-kt = 0.05 を満たす t を求めるためには:

t = t1/2 ・ 2.9957 / -0.6931
≒ t1/2 ・ 4.32
この結果に基づいて、定常状態に到達するまでの時間は、消失半減期の約4.32倍と計算されますが、実際の薬物動態学では、便宜上「約5倍」とすることが一般的です。
これは、より安全なマージンを考慮したものであり、また、定常状態への到達についての厳密な数学的証明よりは、経験的な観察に基づいています。
したがって、定常状態に到達するまでの時間が消失半減期の5倍とされる根拠は、薬物が体内で十分に平衡に達するまでに必要な時間の経験的理解に基づいています。
論点解説2 定常状態の血中濃度 C_ss と点滴速度 R_0 、分布容積 V 、そして消失速度定数 k との関係を証明する
定常状態の血中濃度 C_ss を点滴速度 R_0 、分布容積 V 、そして消失速度定数 k によって表す関係を証明します。
1: 点滴静注の基本方程式
点滴静注が開始した後の血中濃度 C(t) の変化は、以下の微分方程式で表されます:

ここで、
dC(t) / dt は時間 t における血中濃度の変化率。
R_0 / V は点滴速度に対する分布容積の比で、薬物が体内に入る速度。
k ・ C(t) は消失速度で、薬物が体内から出ていく速度。
2: 定常状態の条件
定常状態 C_ss では、薬物の投与速度と消失速度が等しくなるため、血中濃度の変化率 dC(t) / dt は0になります:
dC(t) / dt = 0
したがって、

3: 定常状態の血中濃度 C_ss の解
上記の式を C_ss について解くと:

これが定常状態での血中濃度 C_ss を表す基本的な関係式です。
まとめ
薬物の体内動態を表す微分方程式を設定。
定常状態においては、薬物の投与速度と消失速度が等しいという条件を適用。
その条件を満たす血中濃度を求める。
この手順により、点滴静注において定常状態での血中濃度 C_ss が

であることが示されました。

必須問題の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 必須問題 第106回-第109回 一覧 powered by Gemini 1.5 Pro, Google AI Studio & GPT4, Copilot|matsunoya (note.com)
薬学理論問題【薬剤】(1) の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 薬学理論問題 薬剤(1) 第106回-第109回 31問 powered by GPT4o, Chat GPT|matsunoya (note.com)
お疲れ様でした。
🍰☕🍊
では、問題を解いてみましょう!
すっきり、はっきりわかったら、合格です。
第108回薬剤師国家試験|薬学理論問題 /
問173
一般問題(薬学理論問題)【薬剤】
問108-173
Q. 薬物A 200mgを患者に急速静脈内投与したところ、投与直後と2時間後の血中濃度はそれぞれ20μg/mL及び4μg/mLであった。同じ患者に薬物Aを点滴静注し、定常状態における血中濃度を15μg/mLにしたい。定常状態に達するまでの投与量(mg)と点滴時間(h)の組合せとして最も適切なのはどれか。1つ選べ。ただし、薬物Aの体内動態は線形1-コンパートメントモデルに従うものとし、定常状態に到達するまでに要する時間は消失半減期の5倍とする。また、ln 2 =0.693、ln 5 =1.61とする。

投与量(mg)|点滴時間(h)
■選択肢
1. 60|1
2. 120|1
3. 120|2
4. 360|5
5. 600|5
楽しく!驚くほど効率的に。
https://note.com/matsunoya_note
お疲れ様でした。
🍰☕🍊
またのご利用をお待ちしております。
ご意見ご感想などお寄せくださると励みになりうれしいです。
note からのサポート、感謝します。
今日はこの辺で、
それではまた
お会いしましょう。
Your best friend
Mats & BLNt
このコンテンツ
松廼屋|論点解説 薬剤師国家試験対策ノート問108-173【薬剤】論点:線形1-コンパートメントモデル / 点滴静注 / 定常状態|matsunoya (note.com)
Here; https://note.com/matsunoya_note/n/n2c2c18679143
よろしければこちらもどうぞ
このコンテンツの制作者|
滝沢幸穂(Yukiho.Takizawa)phD
■Facebook プロフィール
https://www.facebook.com/Yukiho.Takizawa
■X (Former Twitter) プロフィール 🔒
https://twitter.com/YukihoTakizawa
CONTACT|
mail: info_01.matsunoya@vesta.ocn.ne.jp (Matsunoya Client Support)
tel: 029-872-9676
日々の更新情報など、Twitter @Mats_blnt_pharm から発信しています!
🔒 🐤💕 https://twitter.com/Mats_blnt_pharm
https://note.com/matsunoya_note
note.com 右上の🔍で
( matsunoya_note 🔍 )
松廼屋 Mats.theBASE
https://matsunoya.thebase.in/
サポート感謝します👍
最後までお読みいただきましてありがとうございました。
Here; https://note.com/matsunoya_note/n/n2c2c18679143
松廼屋|論点解説 薬剤師国家試験対策ノート問108-173【薬剤】論点:線形1-コンパートメントモデル / 点滴静注 / 定常状態|matsunoya (note.com)
ここから先は
¥ 700
医療、健康分野のリカレント教育における「最強コンテンツ」を note で誰でもいつでも学習できる、 https://note.com/matsunoya_note はそんな場にしたい。あなたのサポートがあれば、それは可能です。サポート感謝します!松廼屋 matsunoya
