Threads 過去投稿まとめ5 色々な=と"同じ"
数学的な "同じ" には小中高で習った「値が同じ」以外にもいくつかあります。
分野に依りますが、同じとみなすことができるものを同じものみなして、
「異なるものは何種類か。」
「与えられたものがどれと同じかを判定せよ。」
という未解決問題が各分野にあります
等式の種類
定義式 A=B AをBで定義する
(一般には A := Bとかかれることが多い)
恒等式 f(x)=g(x)
どの変数がどんな値でも成り立つ式
方程式 f(x)=g(x)
等式が成り立つようなxを探す「問題」を表す
計算式 左辺を計算すると、右辺になる
同値関係
集合X上の2つの元(要素)の組で、以下条件をみたすもののことです!
a~a
a~b ならば b~a
(a~b かつ b~c) ならば a~c
等号=の一般化になっています
分野にかかわらずどこでも出てきます
例えば、整数の≡について a≡b mod m は同値関係です
同値な命題
2つの命題P, Qの真偽が互いに一致することを言います!
厳密には、
PからQが示せて、かつ、QからPも示せるとき、
PとQは同値である、と言います
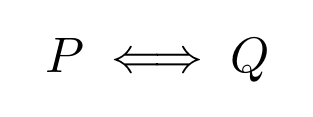
記号では、P⇔Qと書きます
「同値関係」とは別の概念なので注意が必要です
命題の同値は、同値関係を満たします(ややこしい)
同型
ざっくりと、2つの集合と構造が同じで同一視できるとき、 その2つは同型であるといいます!
分野によって同型の意味が異なりますが、多くの分野では
構造を保つ全単射な写像が存在すること
が定義になります
同型なものと同型でないもの分類は、数学の多くの分野で研究されています
非投稿
例えば、群という数学的な構造があります。主に対称性と関連性が高い分野です。
2つの群が同型であるとは、準同型かつ全単射な写像が存在する、と定義されています。
有限群は、10000ページ以上の論文により完全に分類が完了しています。
例えば、結び目理論。
異なる結び目はいくつあるのか?はまだ未解決で研究されています。
