
やさしく学ぶ統計学~四分位数とその可視化~
↓↓↓動画で見たい方はこちら↓↓↓
みなさんこんにちは。和からの数学講師の伊藤です。前回はデータを要約する代表値について、平均値と中央値をご紹介しました。
今回は、中央値と同じく順序に基づいた代表値ということで、四分位数とその可視化をお話していきます。
この記事の主な内容
1. 四分位数とは
中央値は、データを小さいものから並び替えたときに、順序的にちょうど真ん中にあたるデータでした。ここからご紹介する四分位数も、このように順序に基づいた統計量です。
今回は、無作為に選んだ14個の市町村におけるコンビニの数のデータを見ていきます。

右側のデータは、コンビニの店舗数が少ない順に地域を並べ替えたものです。中央値は7番目と8番目のデータの平均をとって計算することになります。このデータは中央値を計算すると30となっています。

では次に、このデータを小さい順に並べたときの下半分にあたるデータと、上半分にあたるデータに分割して考えてみます。

下半分のデータの中央値は、4番目にあたる16です。この、最小値から中央値までのデータの中央値が、第一四分位数と呼ばれる指標です。順序で見ると小さい方から数えて25%目の位置にあるため、25%点とも呼ばれます。
同様に、中央値から最大値までのデータの中央値を求めると、56となります。この値は、第三四分位数(もしくは75%点)と呼ばれます。また、中央値のことを第二四分位数や50%点と呼ぶこともあります。

第一四分位数、第二四分位数、第三四分位数を総称して四分位数と呼びます。
2. 箱ひげ図
データの最小値、第一四分位数、中央値、第三四分位数、最大値を同時に可視化することができるグラフとして、箱ひげ図と呼ばれるものがあります。
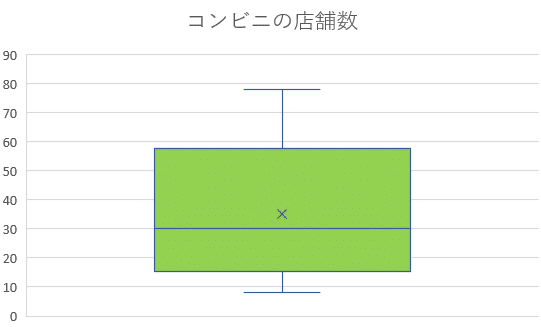
第一四分位数から第三四分位数までを箱で囲み、中央値に線を引きます。最後に箱から最小値、最大値にひげを伸ばすことで完成となります。また、平均値の位置をバツ印などで表現することも多いです。
箱ひげ図は、データがどの位置に偏っているかという情報や、データの散らばり具合を可視化できる便利なグラフです。同時に複数の箱ひげ図を並べて比較することにも長けているので、覚えておくとデータの可視化の幅が広がります。
3. 最小値と最大値について
箱ひげ図を作成する際にデータの最小値、最大値を考えましたが、これらの値をチェックしておくことで、データの範囲やデータに異常な数値がないかどうかといった点を事前に確認することができます。
数字のデータである“量的データ”を扱う際には、まず最小値・最大値から確認する癖をつけて、分析のミスを減らしていきましょう。
●四分位数の定義は一つではない?
ここまで四分位数に関してお話をしてきましたが、データが奇数個の場合に四分位数を計算しようとすると、場合によっては途中で迷ってしまう部分があるかもしれません。データが奇数個ある場合、順序的に真ん中のデータは一つに決まります。ここで、第一四分位数(下半分のグループの中央値)を求めたいのですが、中央値は「下半分」に含めるべきなのでしょうか…?
こういった問題について、四分位数には異なる定義が存在します。以下の記事では、その定義の違いについて詳しくお話していますので、興味のある方はぜひご覧ください!
●和からのセミナー案内
和からではデータ分析に関するセミナーを多数用意しています。興味のある方は是非一度無料講座へお越しください。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/伊藤智也>
