
2023年度入試 市西グローバル・サイエンス科問題分析【数学】
この記事で紹介するのは、ずばり3点
2023年度 市立西宮高校グローバル・サイエンス科、数学の問題分析
実際の入試問題の紹介
夏休みからの学習法
です。
市立西宮高校グローバル・サイエンス科の合格者数が19年連続No.1の開進館による問題分析をぜひともご覧ください。
2023年度 市立西宮高校グローバル・サイエンス科・数学入試問題の概要
大問1 小問集合 配点:25点
(1) 根号の計算のくふう
(2) 2次方程式の計算
(3) 素因数分解
(4) 標本調査 枝問4題、すべて記述大問2 文章題【やや難】・放物線と直線 配点:25点
大問3 円と平面図形 配点:25点
大問4 座標と規則性 配点:25点
※ 市西グローバル・サイエンス科は開示された答案をもとに作成しています。
大問1 小問集合
大問1は例年通りの小問集合の出題です。A4サイズ用紙2枚分の分量です。
(1)は、根号の計算のくふうです。例年の出題傾向に沿った問題です。難易度はそれほど高くはありません。
例題をこちらに記載しておきます。一度チャレンジしてみましょう!
$${\sqrt{25^2-7^2}}$$を計算しなさい。
【解答】
$${\sqrt{25^2-7^2}}$$
$${=\sqrt{(25+7)(25-7)}}$$
$${=\sqrt{32}\times\sqrt{18}}$$
$${=4\sqrt{2} \times 3\sqrt{2}=24}$$
(2)は、2次方程式の計算問題です。解の公式を使えば解くことができますが、$${b}$$の係数が偶数なので、$${x=\displaystyle \frac{-b\pm\sqrt{b'^2-ac}{}}{a}}$$を使うと計算ミスが減るでしょう。
(3)は素因数分解の問題です。開進館の授業を受けていた人は、2023という数字が特徴のある数字だと授業で伝えていたので、全員正解できていたでしょう。
(4)は標本調査に関する問題です。標本調査と全数調査の違いやその意味を記述させる問題が出題されています。
標本調査…調査の対象となる集団の一部分を調べて,集団全体傾向を推測する調査
多くの手間や時間、費用などがかかる場合や食品の品質、工場の製品の良否などを調べるのに、製品をこわすおそれがある場合におこなわれる。
全数調査…調査の対象となる集団全部について調査すること。
大問2(1) 文章題 速さに関する問題
速さに関する問題が出題されています。登場人物が2人登場し、2点間の途中で折り返す問題です。ダイヤグラムを自分で書くことができれば解くことができるでしょう。
例題をこちらに記載しておきます。
弘君と学君がA地点から12㎞離れたB地点へ行くのに、弘君は車に乗せてもらい、学君は徒歩で同時に出発した。途中、弘君はP地点で車から降ろしてもらい、徒歩でB地点へ向かい、車は引き返してQ地点で学君を乗せてB地点へ向かった。そして、学君は弘君の16分後にB地点に着いた。ただし、車の速さは時速36㎞、徒歩の速さは時速4㎞とする。このとき、次の問いに答えなさい。
(1) A地点からP地点までの距離を$${x}$$km、A地点からQ地点までの距離を$${y}$$kmとして、連立方程式をつくりなさい。
(2) $${x}$$、$${y}$$を求めなさい。
(2003 弘学館)
大問2(2) 放物線と直線
座標を文字で置き、座標を計算して解く問題が出題される傾向にありますが、2023年度入試では、
・中点連結定理の性質を用い、
・直線の傾きを文字式で表し、
・三角形の面積を2等分する直線の式を求める。
といった、文字計算と図形の知識を背景としたバランスのよい問題でした。
三角形の面積を2等分する直線の式を求める問題では、やや難易度が高い「頂点を通らずに三角形の面積を2等分する」問題が出題されていました。
地道に計算しても解ける問題ですが、開進館で指導している以下の性質を学習している人は、短時間で解くことができたのではないでしょうか。
1つの内角が共通な三角形の面積比
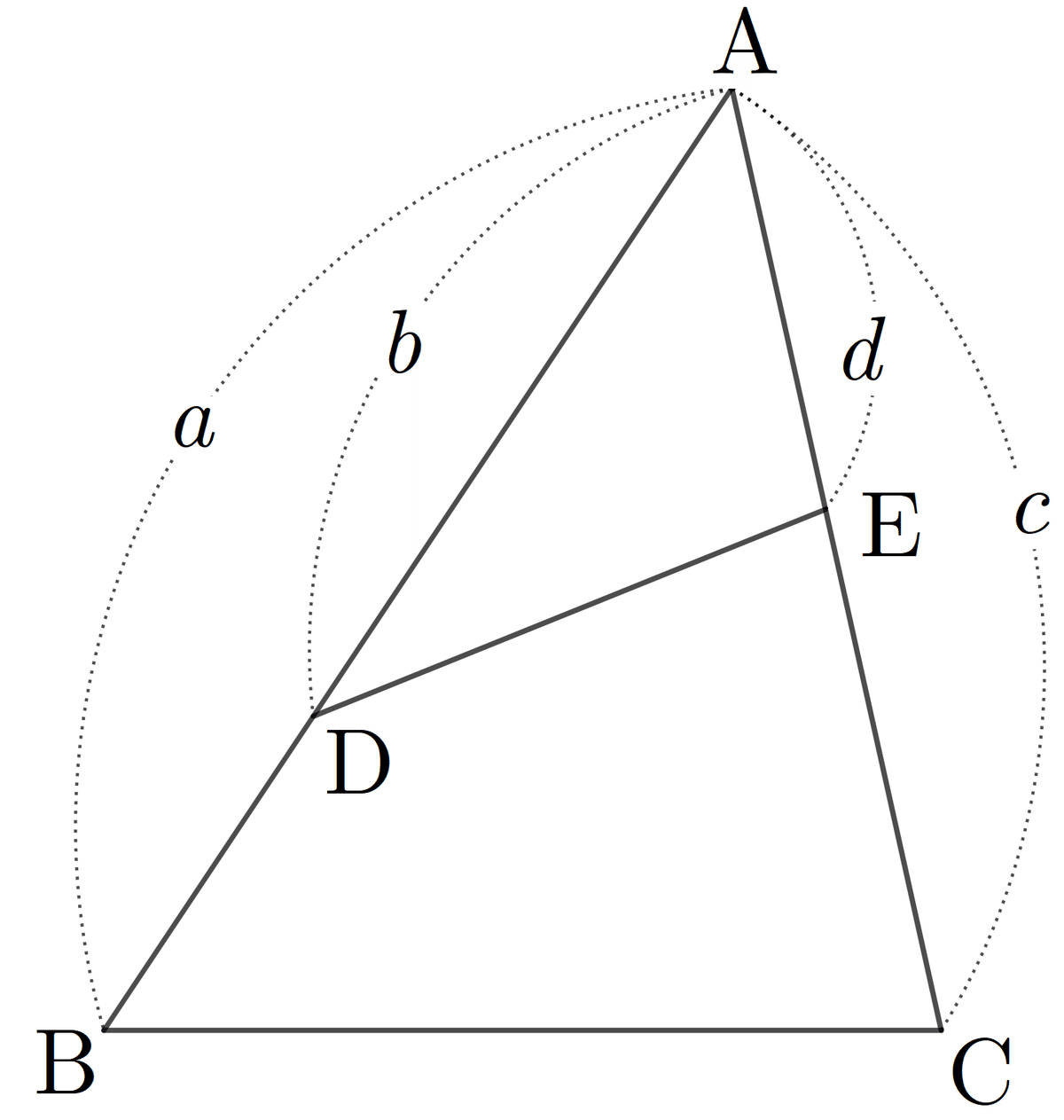
$$
\triangle ABC : \triangle ADE=ac:bd
$$
大問3 円と平面図形
円に内接する三角形や、円に外接する六角形が登場する図形問題です。
特別角(30°、45°、60°)と三角形の三辺の比
正三角形の面積公式
が分かっていれば、さほど難易度が高くはありません。
例題を記しておきます。
下の図において、大きい円の半径は小さい円の半径の何倍ですか。

大問4 座標と規則性
近年の市立西宮高校グローバル・サイエンス科の数学の入試問題で頻出の、「大学入試共通テスト型、誘導空所補充問題」です。
座標平面上にあるルールで点を取ると、それが規則性を帯びるという問題です。
具体的には、具体的事象から、
$${1+3+5+ \cdots+(2n-1)=n^2}$$
という一般性を引き出しましょうという問題です。
ここでの注意事項は、記述内容が間違っていなくても、設問に適切に答えていなければ、不正解になるということです。
理科でも同様ですが、設問で問われていることに正確に答えるという「国語力」が問われることになります。
夏休みからの学習法
市立西宮高校グローバル・サイエンス科の数学の入試問題は、神戸高校総合理学科の数学の入試問題とは違い、難関校特有の特別な思考過程や解法を要求される問題はあまりありません。
正確な座標文字計算
教科書+αレベルの図形的知識
発想力 ※極端なものは不要
記述力
が問われます。
したがって、中3の9~10月ごろまでに中3内容を終了し、あとは過去の入試問題を活用し、実践演習をしていくのがいいでしょう。
時間を計測し、文字式を中心とした計算処理能力を高めておくことと図形の標準~応用の問題に慣れておくことが重要です。
何を学習したらいいのかわからない人に
市立西宮高校グローバル・サイエンス科の入試問題の紹介をしてまいりましたが、過去問が手に入りづらい上に、何を勉強したらいいのかわからないというのが実際のところでしょう。
開進館は市立西宮高校グローバル・サイエンス科の合格者数が19年連続No.1で、合格のノウハウをしっかりと蓄積しております。
開進館では昨年度から、市立西宮高校グローバル・サイエンス科に特化したオンデマンドWEB講座を開講しております。
記述力や発想力を鍛えることができる数学の教材や、実践力を高める理科の教材、小論文の対策など準備を万全にできるコンテンツがそろっています。
夏休みの時間のあるときにWEB講座を受講して、合格をしっかりと手繰り寄せましょう。詳細は以下からご覧ください。
