
カルノー図を初めて習ったのでちょっと使ってみた!
はい!どーも!!まっちゃんです!
今回はデジタル電子回路で出てくるカルノー図をちょっと練習してみた!って実況noteですw
カルノー図の使い方を授業で習ったので、そのアウトプットみたいな感じで書いていきます!
完全主観で、内容が分かりにくいところもありますが、もし内容をしっかり学びたいという人はそのようなサイトや動画を見てください!
どちらかというと問題を解きながらあーだこーだ言っていくだけの記事になってるので、暇つぶしにでもあなたの復習がてら見ていただけたらなと思ってます!
この記事を通して、一緒に学ぶ仲間ができたら嬉しいです!!
それでは本編へ行ってみましょう!!
<今回の課題>
今回僕に出題され課題は問題1が15問、問題2が2問、問題3~7が1問ずつの合計22問だ!
望むところだぜ!!
さあ、最初の問題1はこんな感じ
「以下のカルノー図を簡単化した出力fの論理式を表せ」
というわけで最初にボクの前に出てきたカルノー図がこちら

しかしここでボクはこんなことを思ったわけだ
「この図ってどゆ意味だっけ??」
ポイントは縦と横の列に書いてある文字だったかな
あーそうそう!空欄は「0」が入るんだったな!
ってことは「AかつBかつC'(これCの補集合って意味です~)」に1、「AかつB'かつC'」に1、「A'かつBかつC」に1、「A'かつB'かつCに1」、「A'かつBかつC'」に1、「A'かつB'かつC'」に1で合計6つに1が入ってる!
カルノー図のルール(2の累乗のグループに分ける)に従ってこの1を囲ってみるか
そーするとこんな感じになるかな
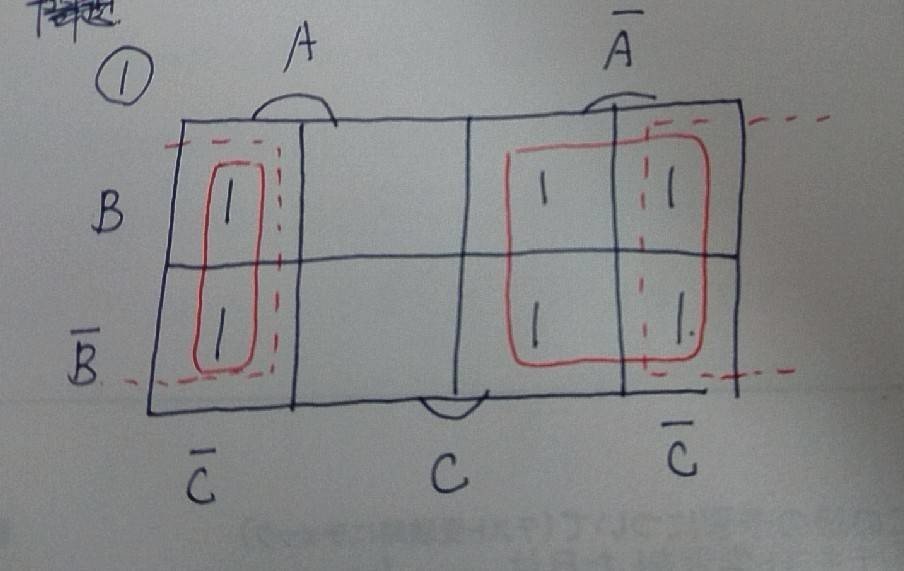
2の1乗個のグループと2の2乗個のグループが作れたね~
たしかこの次にやることはグループで囲った文字の矛盾点を排除していく作業だったな!
例えば左側の実線で囲まれたグループはBとB'が共存してるから矛盾してる!
これは無視すると「AかつC'」が残るね!
同じように右の実線で囲んだグループを見てみると、BとB'、CとC'が共存してるのはおかしいから「A'」だけか
点線のグループはAとA'、BとB'が共存してることになるからおかしいね!ってことは「C'」が残る!
つまり答えは「f=AC'+A'+C'」か!
はい!2問目!!
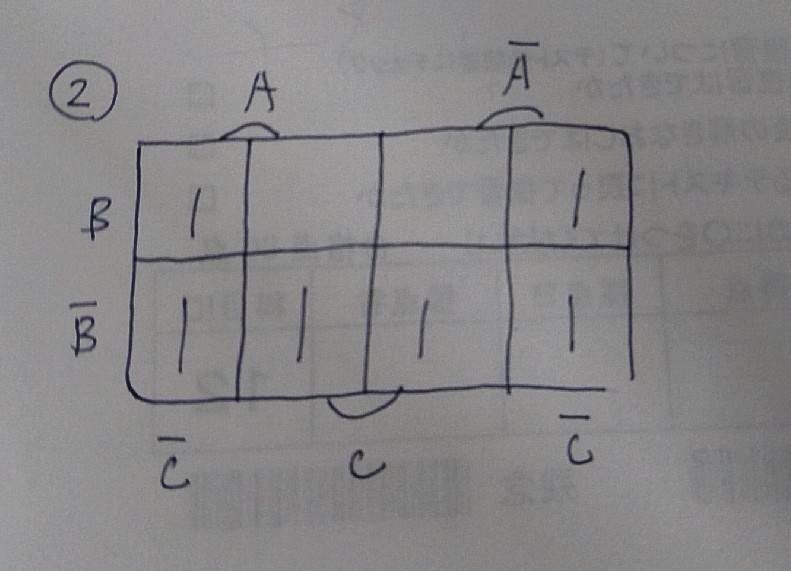
なるほどなるほど!
よし!グループ分けしてみよう!!

ちょっと実線のグループ分けがミスったけど気にしないw
ということで実線のグループを見ていくと、
BとB'が矛盾!AとA'が矛盾!ってことで「C'」やな!
点線グループも見ていこう!
明らかにCとC'が矛盾wあとAとA'がいるのもおかしいな!ってことは「B'」B'や!
つまりこの答えは「B'+C'」ってことか!
なんかやってて思ったけど、2つの1を囲ったら矛盾は1つ、4つの1を囲ったグループには矛盾が2つあるって法則成り立ちそーな感じする!(まあ、文字が3つの場合限定だろーけどさ!)
さあ、つぎつぎ!!

これもサクサクグループ分けしてみるよ!!

で、、出たーーー!!!ねじれ!!
ねじれっていうのはXORを作り出す関係だったね!
あ、でもXORってどんな関係だっけ??
そーだそーだ!「ab'+a'b=a⊕b」だった!
今回はこれが出てくるんだな!よしよし...ってあれ??
「f=BC+B'C'」になる!!
これはXORじゃない...どこかでミスっているのか??
ん~...ミスは見当たらないなぁ
ちょっと色んな資料を漁って調べてみるかー
(数分後...)
分かった分かった!!ボクのカルノー図は間違ってないわ!!
これはXNORを表していたんだね!
あんま使ったことないから出てこなかったよ~w
XORっていうのは「ab+a'b'=(a⊕b)'」の関係のことを指すらしい!
そんなんあったな~w
実際に使う機会があんまりなかったから忘れてたわ!
ということで今回の答えはこんな感じかな!「f=BC+B'C'=B⊕C」
次へ行きましょう!!
4問目!!

ささ、グループ分けですよ!

またなんかねじれがあったり複雑になってんな~
とりあえず落ち着いていつも通りやっていきましょ!
まずは点線から!これは「C'」ですね!
左側の実線で囲ったグループは「AB」かな
右側の実線で囲ったグループは「A'B'」で、この実線で囲った2つのグループはねじれの関係になるからXが付くわけだね!(XORとXNORだ!)
つまり「f=C'+AB+A'B'=C'+(A⊕B)’」だ!!
いいね~いいね~!分かってきたじゃん!(これで間違ってたら恥ずかしいw)
ネクスト!!5問目!!
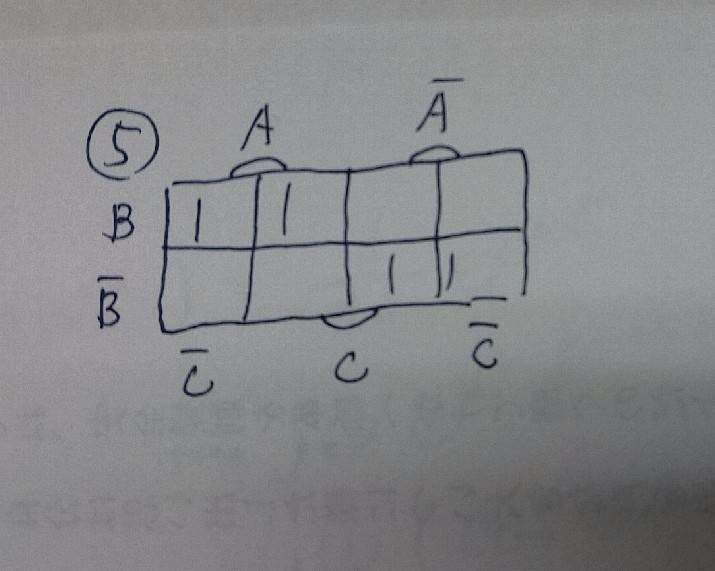
あーもうイージーですわ!(笑)
グループ分けしていくとこーだな!!

なんかねじれを見てもビビらなくなってきたぞ!!
論理式はこーだ!!
「f=AB+A'B'=(A⊕B)’」だな!!
次!6問目~!!

ねじればっか!!なんかちょっとくせ者??
とりあえずグループ分けだな
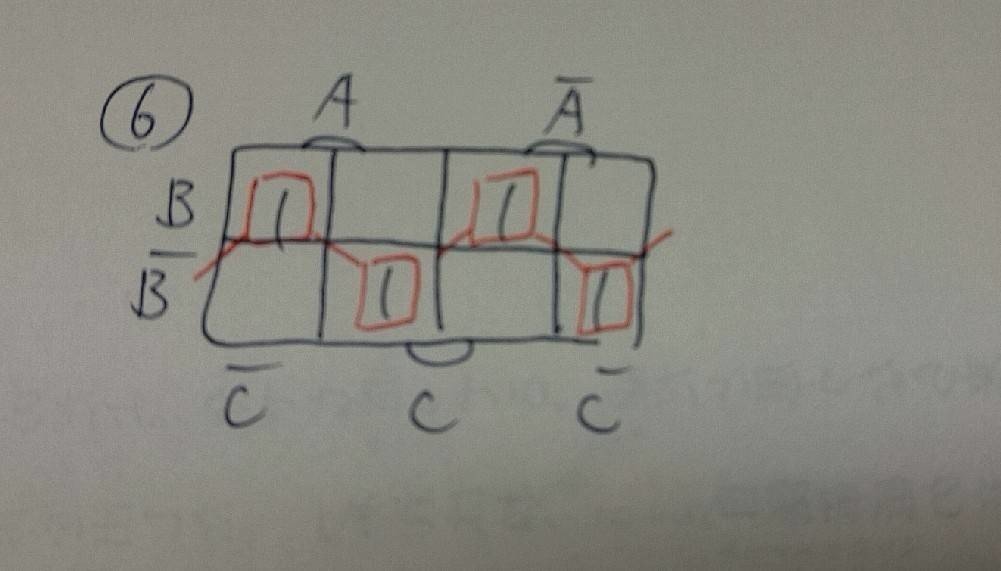
そうそう!忘れちゃいけないのは「2の累乗個単位でグループ分け」するんだけど、1も「2の0乗」だから入るんだよね!ただこれはグループではないなww
さて、どんな形になるのか予想が付かないけどとりあえずいつも通りやってみるよ!
「f=AB'C'+AB'C+A'BC+A'B'C'」になるのか~
なるほど、矛盾する箇所がないんだね!
でもこれで終わりではないはずなんだ!だってねじれの関係にあるブロックがあるんだから「XOR」の形で表せるはず!だけどなんだか雲行きが怪しくなってきたぞ~w
えーっと、とりあえず論理式にしてみると
「f=AB'C'+AB'C+A'B'C=AB'(C'+C)+A'C(B+B')=AB'+A'C」
おっとwつまりあんたたちどーゆー関係や...??
Xが入るのは分かる!だってカルノー図はねじりまくってるから
(数分リサーチ...)
ちょっと分からなかったのでとりあえずパスで!
ということで次の問題へ行きましょう!
7問目です!!

うおっ!!なんか増えた!!!
でもきっとやることは変わらないはず!それではグループ分けしていきましょっ!

またちょっと点線の囲みがミスってるので、ちょっと見にくいけどご勘弁w
実線が2つと点線が1つ!ちなみにこの囲み方のルールを紹介する時に2の累乗個単位って話をしたんだけど、あれは正確じゃないねw
縦と横のマスの個数が2の累乗個って言った方が正確だったか!
ということで今回は2×4のグループが誕生していますよ!!
さて、論理式にしてみましょーか!
なんだか数が多くてさっきのようにはサクサクっとはいかないなぁ
左の実線グループは「A」かな、右の実線グループは「A'C」、点線のグループは「C」だね!
つまり「f=A+A'C+C」だ!きっとw
次は8問目!よーやく半分だ

わーなんか逆さになった階段みたい
とりあえずグループ分けへ

ちょー見ずらいし!!!
あまりの見ずらさに色を追加してしまったw
さあ、論理式はこんな感じか
「f=BD'+A'C'+BC+A'B+A'D」合ってるよね?w
自信なくなってきたけどこれ以上簡単にできないと思うし...
でもさ~ここまで解いてて思ったけど、カルノー図すごいよね!
ふつーに論理式だけで全部簡単にしよーと思ったら吸収則やら分配則やら駆使してやってかないといけないでしょ?
文字が4つとかになってきたらもうやる気なくしそう~
さて、お次は9問目です!なんだか終盤に近付いてきましたな!

なんかいけそうやな!グループ分けしてみるとこんな感じか

ねじれ祭りっすね!また6番の悪夢が頭をよぎるけどとにかく論理式にしてみるよ!
「f=ABD'+A'BD+AB'D+A'B'D'=A(BD'+B'D)+A'(BD+B'D')=A(B⊕D)+A'(B⊕D)'」
あ、今度はいい感じにまとめられた!
XORとXNORの式変形が慣れてきたのか、使えそーなとこが分かるよーになってきた!
この調子で10番!!

グループわけしてみよーか

2×2のねじれだね!まあ、でもやること変わんないっすからw
「f=AB+A'B'」これはXNORの形だから「f=(A⊕B)’」っすよね!
はい!11番!

なんか1いっぱいw数え間違いしないよーにしないとね~

やってみると意外とシンプルwwホントにこれで合ってる??(笑)
まあ、ざっと見た感じ大丈夫そうなので論理式へ
「f=C+D」
ホントに合ってる!???再び心配になってきたが、次へ進みますね~
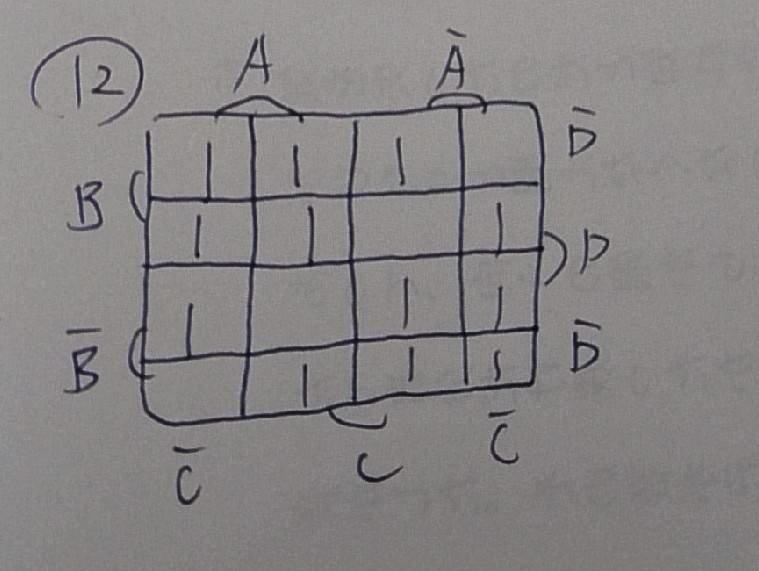
うわ~数え間違いが起きそう...
慎重にいきましょう!!

縦と横がつながっているという発想をしばらく忘れていたからまさかの不意打ち!今までここ見逃してなかったか不安になった
ねじれの線を書き忘れたけど、落ち着いて論理式へ
実線グループは「AB+A'B'=(A⊕B)’」
点線グループは「C'D+CD'=C⊕D」
いや~やっぱ離れてると見にくいな!
ということで「f=(A⊕B)’+C⊕D」かな!
さあ、次や!!

ああ、なんか簡単に見えるwwということでグループ分け!!

なんかこれはぱっと見で分かるよね!(意外とこーやって油断してる時が一番注意だったりする)
論理式はこーでしょ!
「f=BD'+B'D=B⊕D」
あれ?ねじれ??なんかねじれの定義をもう一度確認してみたくなってきた
これめっちゃ不安だわぁ
14番へいきましょう

あ、今度は縦になった
ってことはさっきの不安がもう一度来るわけか~これ大丈夫なのかなぁ

まあ、こーなるでしょーね~
ってことは論理式はこーなるでしょーね~
「f=AC+A'C'=(A⊕C)’」
うん、知ってたw
これねじれ~~???図形的に大丈夫なのかなぁ
っと自分のねじれに関する知識を疑っていると問題1の最後!
15問長かったなぁ
最後くらいはねじれもなくて、簡単な問題解いてスッキリしてから終わりたいよね!
ということでラスト問題はこちら!!

「・・・」
おいいいーーマジかぁ
6問目と似てるパターンじゃん...(すべて単品ですべてねじれ)
これさ~論理式ににはできるんだよ??
そのあとうまくXORとかXNORの形にできないんだよなぁ
まあ、当然グループ分けはこーなるじゃないですか~

問題はこっからだよなぁ
いちおう論理式にしてみるよ~
「f=ABC'D'+A'BCD'+ABCD+A'BC'D+AB'C'D+A'B'CD+AB'CD'+A'B'C'D'」
(数分後...)
いや~ちょっとお手上げだわw
多分、ブール代数の基本的な計算法則の知識が抜けてるのかもだけど、けっきょくどこが問題なのか判明しませんでした
さて、今回は問題1を解いてみましたが、意外とルールさえ掴めちゃえばサクサク進みましたね!
まあ、一部できなかったところもあったんですけど、もし分かる人いたら教えてほしいです
また、ボクは合ってると思い込んでいるところも間違ってたりすると思うのでその辺も気づいたらこっそり教えてほしいですw
まだあと7問目まであるんですけど、ここまで多くの作業を要する問題ではなさそうなので、一気に行けたらいいなっと思ってます!!
電子回路系の話って目に見えないから分かりづらいっすよねw
パズルみたいに解いていくのがいいのかなとも思いますが、一緒に学ぶ仲間が増えてくれたら嬉しいです!
