
データを「幅」で捉えることで現状把握と分析の精度を高める
事業成長のためには適切な現状把握が重要
事業の成長を考えていく上で、「今何が起きているか?」を正しく把握することは重要です。
なぜなら、正しい事実を把握するからこそ、正しい課題や打ち手を出すことが出来るからです。逆に現状把握を間違えると全て誤った方向に進んでしまうので危険です。
現状把握や分析、仮説の根拠には”データ”が使われるのが一般的ですが、データには常に”バラつき”があります。
この”バラつき”とは、例えば「クラスで行うテストの点数には様々な点数があり散らばっている」ことや「そのテストの点数の散らばり方はクラスによって違う」などの不確実性のことを指しています。
この”バラつき”まで含めて把握することが出来れば、「今何が起きているか?」の理解度は高まります。
そこでこの記事では、統計学をそこまで学んだことがない人を対象に、データを「幅」で捉えることで現状を正しく理解する考え方について記載していきます。
※私は統計の専門家ではありませんが、少しでもわかりやすく、実務に使える解説がしたく記事を作成しています。おかしいところがあれば是非ご指摘下さい。
また、この記事では概念的な説明に留めております。数式などを詳しく見たい方は専門書などを参照ください。
多くの人は代表値だけ(主に平均)で現状を理解しようとする
まず代表値とは下記の3種類の値を指します。
■平均値(算術平均)
データの合計をデータの個数で割った値
例)クラスのテストの点数の合計÷クラスの人数=クラスのテストの平均点
■中央値
データを大きさ順に並べたときに、真ん中にくる値
例)31人のクラスで、テストの点数を高い順に並べた時の16番目の生徒の点数
■最頻値
データの中で最も出現する頻度が多い値
例)クラスのテストの点数のうち、75点を取った生徒が最も多い=最頻値は75
これらのうち、特にビジネス指標では平均値が多用されているのではないでしょうか。例えば「平均購入単価」や「1人あたり○○数」などです。
多くの人が、事業の現状を把握する数値の一つとして、平均値を利用しています。
また、事業の現状を把握するダッシュボードなどでも、上記のような数値が使われることが多いのではないでしょうか。
集約された数値だけ見ていても、現状は正しく理解できない
代表値は、バラつきがある複数のデータを”代表”しているものです。
逆に、代表されなかった多くのデータたちは、見ている人にその存在を知られていないと考えることが出来ます。つまり、代表値に集約された時点で、そのデータ群の多くの情報は削ぎ落されているのです。
例えば、平均購入単価が5,000円のECショップがあったとします。
とある月の購入人数と単価の内訳をみると、
・2,000円買った人が15人
・14,000円買った人が5人
→平均購入単価は5,000円で購入者は20人
でした。
この情報を知らずに「平均購入単価5,000円」と聞くと
「このお店ではだいたいみんな5,000円くらい買うのか」
と考えがちですが、実際には”2,000円分購入する人たち”と”14,000円分購入する人たち”で成り立っていることに気づくことが出来ないのです。
現状把握を正しくするためには、データの分布を確認すること
だからまず、現状把握をする上で大切なのは、データ全体の分布を確認することです。
同じ”平均購入単価5,000円”であったとしても下記の2つの分布では、「今何が起きているか?」が大きく違うはずです。
↓これは、5,000円付近の購入者が多く、正規分布のように散らばっているパターン
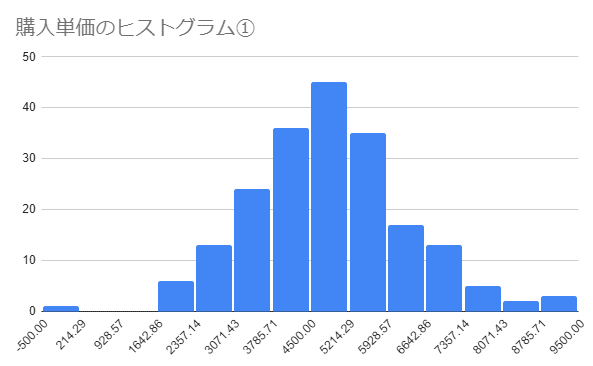
↓これはデータの分布が完全に分かれているパターン
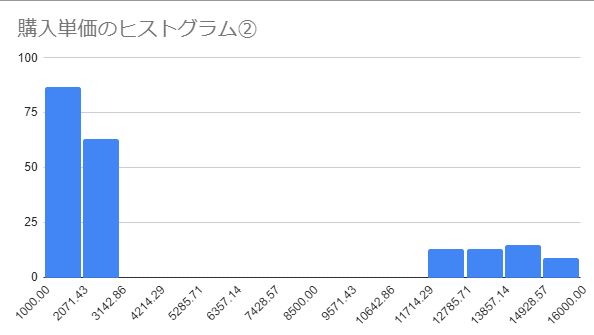
①の場合、「購入者の多くは5,000円程度、購入してくれる」と言い切ってしまって違和感はありませんが、②の場合は果たして「購入者の多くは5,000円程度、購入してくれる」と言ってしまっていいのでしょうか。
確かに平均は5,000円でも、”現状把握”を目的にしている場合、購入単価が低い群と高い群の違い(ユーザー属性や購入している商品など)を調べた方がいいですよね。
データの事前チェック(確からしさや外れ値、欠損値の確認など)も必要
補足になりますが、データから現状把握や分析を行う場合、データの事前チェックも必要になります。これは、間違ったデータを使った現状把握や分析を防ぐためです。
【主なチェック項目】
(1)データがどのようにして作られたものか
(2)データのサイズや各項目の意味や単位
(3)欠損値や外れ値の有無と量
など
(1)に関しては、例えばデータの取得方法がおかしくて信用できるものではないケースもあり得ますので、事前に確認しておくべきです。
(2)に関してはデータの全体像の理解として必要な項目です。
(3)に関しては状況に応じて対応方法が異なってきます。
・欠損値が多い場合
データの信頼性を疑い、取得方法などを確認する
・欠損値がわずかな場合
欠損値を含むデータを除外、もしくは平均値や最頻値などで埋める
・外れ値
その値に意味があるのかどうか考える
本当に意味がない場合or集約する際に影響が大きい場合は除外
あくまでも、現状把握や分析の目的に応じた対応が必要になります。
平均値と標準偏差、信頼区間を利用し、データを幅で捉えることで現状把握と分析の精度を高める
正確な現状把握をするためにはデータ全体の分布を確認することが必須ですが、ビジネスシーンの多くでは、現状を把握して終わることはありません。
現状に対して何かしら施策を打ち、その変化を見て分析をし、新たな施策を考え実行していく、いわゆる”PDCAサイクル”を回していく必要があります。
例えば施策前・施策後のデータの分布を比較する、という効果の検証方法もありますが、平均値や標準偏差、信頼区間の考え方を利用し、データを「幅」で捉えることで現状把握と分析がしやすくなります。
以下、順を追って説明していきます。
データを「幅」で捉える上で押さえておきたい、統計学の基本的な考え方
詳しい説明の前に、データを「幅」で捉える上で前提となる3つの考え方について、概要を記載します。
・母集団と標本
本来知りたいと思っている集団全体:母集団
母集団の情報を推測するために抽出された一部の集団:標本
と言います。
何か調査をする際、本来であればその対象を全て調べたいですが、ほとんどの場合、母集団は非常に大きく、時間とともに変化します(例:日本人全員の身長を調べたい→日本人全員を測定するのは難しい&出生と死亡で対象者が変化し続ける)。
よって、「標本」を利用し、そこから母集団の性質を推測するという考え方が使われます。
詳しくは統計WEBを参照ください。
例えばよく行われる”ABテスト”は、母集団から標本を抽出していることと同じ意味になります。手元にある何かしらのデータは、「標本」に過ぎず、抽出の度に変化するものです。
・確率変数と確率分布
確率変数とは、ある変数の値をとる確率が存在する変数のことです。
そして、確率変数がとる値と、その値をとる確率の対応の様子が確率分布です。詳しくは統計WEBがわかりやすいので、参照ください。
ざっくり言うと、例えばサイコロは1~6の面があり、各面の出現確率は1/6です。1~6の面は、1/6という確率が与えられている変数ということです。
世の中で起きる多くの事象を点で考えた時、それは何かしらの確率が与えられた変数と考えることが出来ます。
確率変数には、一定の確率規則(サイコロで言うと各面の出現確率が1/6)があり、確率分布とは、一定の確率規則を表したものです。
確率分布には様々な種類があります。
・中心極限定理
noteでは数式を記載することが出来ないので、画像にて引用させて頂きます。中心極限定理とは↓ 引用:統計WEB

すごくざっくり言うと、母集団がどんな分布であっても、そこから抽出した標本の平均は、正規分布になるというものです(コーシー分布を除く)。
そして様々な統計手法が、正規分布が前提になっています。
正規分布(normal distribution)とは、”普通の” "通常の" 分布であり、多くの事象がこれに当てはまります。詳しくはコチラ
平均値と標準偏差でデータのばらつきの範囲を把握する
以上の3点を踏まえたうえで、平均値と標準偏差を利用し、データを「幅」で捉えることが出来ることについて、説明します。
標準偏差(=SD)とはざっくり言うと、データが平均値の周辺でどれくらいバラついているかを表す数値です。
こちらのサイトがわかりやすく書いてあるので、詳しく確認されたい方は参照してみて下さい。
例えば現状把握や分析をしたいデータが正規分布に従う場合、平均値±1.96SDの範囲に95%のデータが存在しています。
この±1.96SDの範囲を95%信頼区間と呼びます。
仮にデータが正規分布に従わない場合も、チェビシェフの不等式によって、データのばらつきがどんなものであれ、平均値±2SDの間に3/4以上のデータが存在しています。
この考え方を用いると現状把握や分析の精度を高めることが出来ます。
例えばABテストを実施して、A群とB群の指標を出し、その指標の95%信頼区間を比較すれば、本当に2群に差があるのかどうか、推測することが出来るようになるのです。
データを「点」のみで捉えていると、誤差と呼べるような変化に対して因果を考えてしまうことがあります。それにより生じる意思決定の誤りが積み重なると事業に大きなマイナスが起きることもあります。
逆にデータを「幅」で捉える考え方を身に着け、現状把握や分析の意思決定を高めることが出来れば、事業にとってプラスになります。
具体的な計算方法などに関しては、別の記事でまとめたいと思います。
最後までお読みいただきありがとうございました。
------------------------------------
よかったらtwitterのフォローもどうぞ。
https://twitter.com/MasayukiAbe7
------------------------------------
以下、参考文献です。
