100日後にプロになるワシ23日目（Python）

昨日、機械学習を要約終わらせたが、まだその結果がどれだけ正しいかを分析してなかった。

今日はその分析と改善。
そして最後まで走りきりました！！

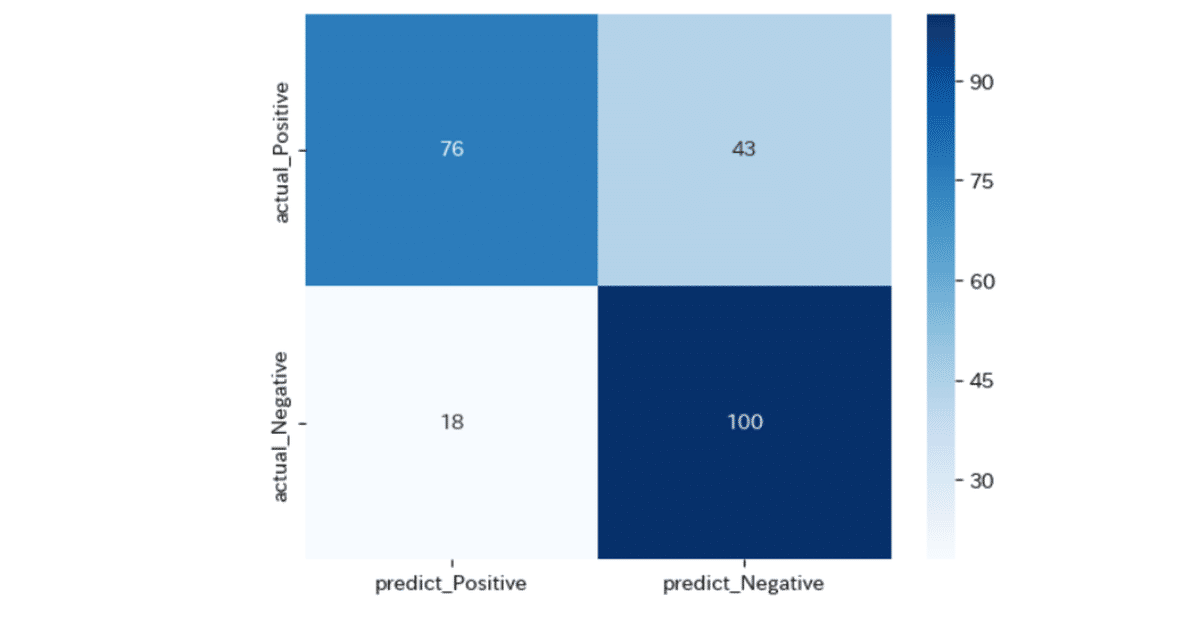
混同行列の計算

今回は疾患があるかどうかの2択なので、予測した結果の疾患があるなし。と実際のデータの疾患のあるなしを比べた表を作成する

これを混同行列といいます。

from sklearn.metrics import confusion_matrix
df_cm = confusion_matrix(y_true=y_test, y_pred=y_pred)

左上から
12
34とすると

1. 疾患ありと予想（事実疾患あり） 74
2. 疾患なしと予想（事実疾患あり）43
3. 疾患なしと予想（事実疾患なし）18
4. 疾患なしと予想（事実疾患なし）100

左上と左下が予想が正解していて、それ以外はハズレ。
中でも疾患ありなのに疾患なしと判定した右上はかなり問題がある

コロナじゃないと判定して、実際はコロナだったら冗談じゃ済まない。。。

ただ、このデータは、疾患ありとする閾値を操作することで変わってくる。

今は疾患の可能性が50％以上だと疾患ありにしているが、判定の確立を20％以上の場合疾患と判断するようにすればそれだけ疾患を抽出できる。

ただこれは問題があって、極端な話全員に疾患ありと判定すれば実際の疾患ありを当てられるように、これでは話にならない。

なので、それらの閾値をちょうどいい値にする指標がある。

ROC曲線の描画、AUCの計算

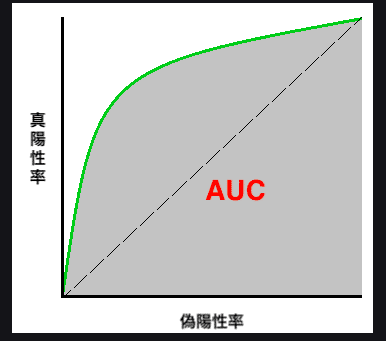
それにはROC曲線を使う

ROC曲線とは、閾値（疾患の有無を判断する基準値）を変化させたときの偽陽性率(False Positive Rate: FPR)と真陽性率(True Positive Rage: TPR)の各点を結んだものです。

そもそも偽陽性率と真陽性率の意味がよくわからんけど

真陽性率は正しく陽性と判断できた割合らしい。
偽陽性率は間違って陽性と判断した割合。

参考：https://bellcurve.jp/statistics/glossary/2014.html

それを計測した結果がこちら

↑この緑の点線が理想。で、ブルーが今の値。

ブルーのラベルにある「area」が1に近いほどいい。
今回は0.827なので割といい方らしい。

こっからさらに改善していく

特徴量を分割するビニング

データによっては、かなりの偏りがあるデータも存在する。

例えば、年齢の人口比でいうと
0歳に近いほど少なく100歳を越えるとほぼいない。（けどいる）

みたいな状況になる。これを1歳ごとに分類して110歳が1人、33歳が5千万人とかするよりは

10代が何人、30代が何人、90歳以上が何人と分割してグルーピングした方がわかりやすい

それをビニングという。
そして、その分割に使うメソッドがbin（ビン）。

では、今回のデータであるT_Billを等間隔でビニング

X_cut, bin_indice = pd.cut(X["T_Bil"], bins=5, retbins=True)
# bin分割した結果の表示
print("binの区切り: ", bin_indice)
print("--- bin区切りごとのデータ数 ---")
print(X_cut.value_counts())

するとこうなる

--- bin区切りごとのデータ数 ---
(0.425, 15.46]    756
(15.46, 30.42]     28
(30.42, 45.38]      5
(60.34, 75.3]       1
(45.38, 60.34]      0
Name: T_Bil, dtype: int64

これで見ると、かなり前半に偏りがあることがわかる。

なので、今度はbinする割合を変更します。

# 境界値を指定したbinの分割
bins_T_Bil = [0, 0.5, 1.0, 100]
X_cut, bin_indice = pd.cut(X["T_Bil"], bins=bins_T_Bil, retbins=True)

0~0.5, 0.5~1, 1~100と分割します

(1.0, 100.0]    441
(0.5, 1.0]      344
(0.0, 0.5]        5

するとほとんどのデータが0.5~1, 1.0以上に分類されることがわかります。

この新しいデータを使って今までのT_Billのデータを変更します。

「0より大きく、かつ0.5以下」 => 0
「0.5より大きく、かつ1.0以下」 => 1
「1.0より大きい」 => 2

のように分類します。

# binの境界値を指定
bins_T_Bil = [0, 0.5, 1.0, 100]
# T_Bil列を分割し、0始まりの連番でラベル化した結果を、X_cutに格納する
X_cut, bin_indice = pd.cut(X["T_Bil"], bins=bins_T_Bil, retbins=True, labels=False)
# bin分割した結果をダミー変数化 (prefix=X_Cut.nameは、列名の接頭語を指定している)
X_dummies = pd.get_dummies(X_cut, prefix=X_cut.name)
# 元の説明変数のデータフレーム(X)と、ダミー変数化の結果(X_dummies)を横連結
X_binned = pd.concat([X, X_dummies], axis=1)
# 結果の確認
print(X_binned.head())

  Age  Gender  T_Bil  D_Bil  ALP  ALT_GPT  AST_GOT   TP  Alb  AG_ratio  \
0   65       0    1.0    0.2  187       16       18  6.8  3.3      0.92   
1   62       1   11.2    5.6  699       64      100  7.5  3.2      0.73   
2   62       1    7.6    4.2  490       60       68  7.0  3.3      0.87   
3   58       1    1.3    0.5  182       14       20  6.8  3.4      0.98   
4   72       1    4.2    2.1  195       27       59  7.3  2.4      0.48   

  T_Bil_0  T_Bil_1  T_Bil_2  
0        0        1        0  
1        0        0        1  
2        0        0        1  
3        0        0        1  
4        0        0        1  

↑TBilのカラムを追加

この新しいデータで再度学習させる

するとこうなった↑

見た目であまりわかりませんがAUCの値が
AUC: 0.8602763139153966

前回の0.82....と比べてUPしています。

なので制度が上がりました！

講座ではここまで。

感想

0.82から0.86まで上がった！と言われても正直ピンとこなかったんですが、
例えば、これが1%で100万円が動くプロジェクトなら400万円利益がでることになりますし、
そもそも、疾患の有無を調べる正確性は1％でも上がった方がいいに決まってます。

なので、出来るだけ精度を上げられるように試行錯誤してやるべき。と感じました。（小並感）