
データの関連性を示す【相関】とは
こんにちは。データサイエンティストを目指して、
統計学を勉強し始めた、駆け出し初心者です。
本日は統計学の基本を学ぶ上で有名な本【統計学入門】を読んで、
特に重要だなと思った【相関】についてまとめていこうと思います。
よろしくお願いします。
相関と回帰の違い
例えば2つの変数xとyがあったとき
相関とは
xとyの間に区別を設けずに対等に見る見方や方法
回帰とは
xからyを見るとき、xからyが決定される様子や程度のこと
というらしいです。
実例を上げて説明すると
身長と体重の関係を見るときは相関
➡︎大きい人って体重も大きい場合がほとんどだよね。
この2つの変数は関連性が高そうだね。って見方が相関。
相関の場合は純粋に
データとデータの関係性を明らかにするのみ。
天気と弁当の売上の関係を見るときは回帰
➡︎晴れると弁当がよく売れるんだよね。
明日は晴れだからこのくらい売れるだろうな。
回帰の場合は、ある一方のデータ(今回は晴れ)が
他方のデータ(売上が大きい)を決定する状態。
といった具合です。
ここまでの話を聞くと、データサイエンティストを目指す身としては
どうしても回帰の方がカッコ良さそうに見えますが、
回帰の基本は相関にあるので、まずは相関をマスターしていきましょう。
めっちゃ相関があるときってどんなとき?
相関には程度があります。
その程度を見比べるには
【散布図】と【相関係数】を使います。
【散布図】
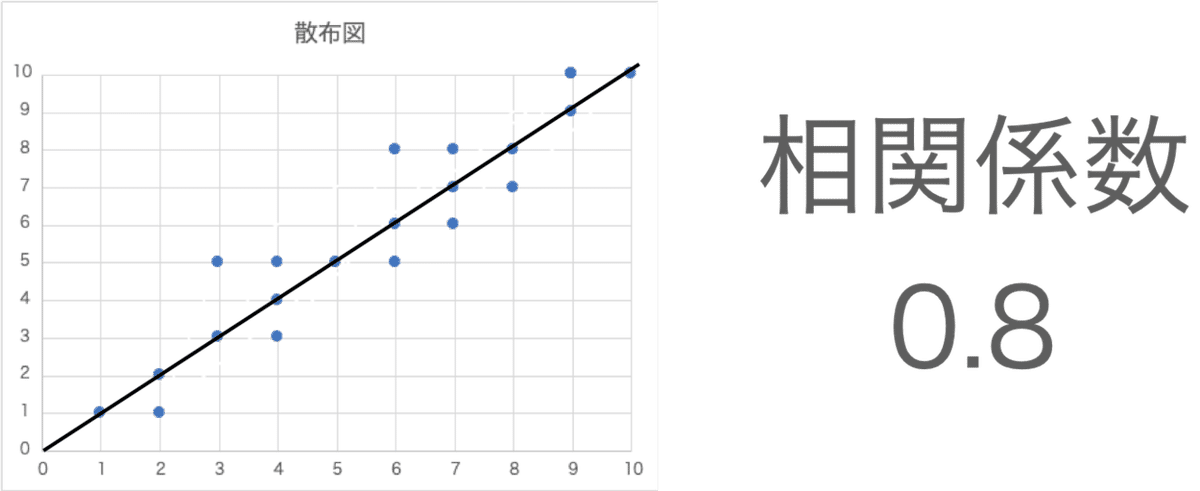
仮にXとYの二つのデータをグラフ化すると
以下の図のようになっていたとします。

こういった場合は
Xが増えるとYも増えるため
2つのデータの間には「正の相関がある」と言えます。
散布図を見ることで、ざっくり相関がありそうか、なさそうか
は
分かりますが、数値的にどの程度相関があるかはわかりません。
【相関係数】
そんな時には相関係数を求めることで
数値的に相関の有り無しを見比べることができます。
求め方はこんな感じ。

共分散と標準偏差の説明は割愛します。
標準偏差については別にnoteを書いてるので、
そちらを読んでもらえると嬉しいです。
ちなみにEXCELでは、CORREL関数を使えば一発で算出できます。
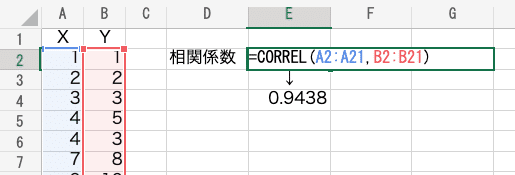
相関係数は −1〜+1 の数値で表されるので
今回の0.94は非常に相関が強いデータといえます。
相関の強さを見るときは必ず
【散布図】と【相関係数】の2つを見ると
視覚的にも、数値的にもデータを見ることができるので
分かりやすく、また誤解することもないですね。
相関係数に騙されるパターン
仮に散布図と相関係数を駆使して、
データ間の相関が高いことを見つけても、それで終わりではありません。
時には見かけ上では相関が強いが、
現実問題その2つのデータ間には相関がないケースがあります。
そのケースとは、第3のデータが
それぞれのデータと強い相関関係にあるケースです。
本書では
新宿にある
・銀行の数
・飲食店の数
・昼間人口
の3つのデータを例に挙げて説明していました。
銀行数と飲食店数のデータから
散布図と相関係数を調べると、強い相関があることがわかったとします。

ただし銀行が多いから飲食店が多いって(逆もしかり)
なんかしっくり来ないですよね。
次に
昼間人口と銀行の数の相関を
昼間人口と飲食店の数の相関を見ると・・・
同じく相関が高い!!
実はこれらのデータは
下図のような関係になっていたのです。

この関係性を見ると納得ですよね。
人が多いから銀行が多い。
人が多いから飲食店が多い。
このように数値的な結果が必ずしも
現実世界の正解になる訳ではないのです。
データを見れるようになったからこそ、引っかかるケースも
あるんですね。気をつけます。
さいごに
データ分析をする際は
基本的に複数のデータを見るケースがほとんどです。
だからこそ2つのデータの関連性を示す【相関】を
マスターすることは、データ分析の第一歩とも言えるでしょう。
まずはご自身が思う、相関が強そうなデータの
散布図と相関係数を算出してみてはどうでしょうか。
