
学校の先生が教育現場で使えるChatGPTテクニック〜シーン2 数学の問題作成〜
学校の先生が必ず行う問題作成について取り上げていきます。今回は数学の問題作成に取り組んでみます。
指導要領とルールの設定
数学の問題を,「平成29年告知の教育指導要領 数学」に則って作成します。
文部科学省の中学校学習指導要領(平成29年告知)開設 数学編 平成29年7月
上記の指導要領から指導要領を引用し、問題として出力して欲しいものとしては下記の通りです。
問題
解答
解説
指導要領の関連項目
さらに、問題作成時のルールとして、下記を追加しました。
問題は後半の問題ほど難易度が上がる構成
最初の3問が選択式の問題
4〜10問目が自分で解答を記入する方式
最後の3問は文章題
以上のことを、下記の2つの方法で実施してみます。
ChatGPT-4のみで数学の問題作成
ChatGPT-4とCode Interpreterで数学の問題作成
結果として、ChatGPT-4とCode Interpreterを組み合わせた方が良いということになりました。それでは、それぞれ見ていきましょう。
ChatGPT-4のみで数学の問題作成
まずは、下記のようなプロンプトを実行します。
あなたは中学校の先生です。下記に指導要領があるので、それを参考に問題を10問作成してください。
# 対象者
中学校2年生
# 科目
数学
# ルール
問題は後半の問題ほど難易度が上がる構成
最初の3問が選択式の問題
4〜10問目が自分で解答を記入する方式
最後の3問は文章題
# 指導要領
文字を用いた式の四則計算
・簡単な整式の加減及び単項式の乗除の計算
・文字を用いた式で表したり読み取ったりすること
・文字を用いた式で捉え説明すること
・目的に応じた式変形
連立二元一次方程式
・二元一次方程式の必要性と意味及びその解の意味
・連立方程式とその解の意味
・連立方程式を解くこと
# 出力
問題:
解答:
解説:
指導要領の関連項目:問題作成と検証
すると、下記のように問題を10問作成しました。上記のルールに基づき、10問の問題を作成しました。
問題1
以下の式の中で、xに2を代入したときの値が最も大きいものを選びなさい。3x - 2
x^2 - 4
2x + 1
5x - 3
問題2
以下の式の中で、yに-1を代入したときの値が0となるものを選びなさい。4y + 4
-2y - 2
y^2 + y
3y - 1
問題3
次の等式の中で、どれが正しいか選びなさい。(a + b) * c = ac + bc
(a - b) / c = a/c - b/c
a * (b + c) = ab + ac
全て
(以下、略…)
問題8
ある数学の試験で、山田君と田中君の2人が全問正解しました。山田君の得点は3x + 4で、田中君の得点は5x - 2です。試験の満点は100点です。xの値を求めなさい。
問題9
妹があるパズルゲームをしています。彼女がステージ1で得たスコアは2y - 3で、ステージ2では3y + 2を得ました。彼女が2つのステージで合計100点を得たとき、yの値を求めなさい。
問題10
あるサッカーチームには、新人がx人、ベテランがy人います。新人の年齢の平均は20歳、ベテランの平均年齢は30歳です。チーム全体の平均年齢が25歳であった場合、新人とベテランの人数の関係を表す連立方程式を立て、それを解きなさい。
答えと解説
問題1:
解答: 4.
解説: xに2を代入したとき、4つの選択肢の値は、それぞれ4、0、5、7となる。したがって最大値は7。
指導要領の関連項目: 文字を用いた式で表したり読み取ったりすること
問題2:
解答
解答: 1.
解説: yに-1を代入したとき、4つの選択肢の値は、それぞれ0、-4、0、4となる。したがって0となるのは1番と3番。
指導要領の関連項目: 文字を用いた式で表したり読み取ったりすること
問題3:
解答: 4.
解説: 配布法則により、全て正しい。
指導要領の関連項目: 文字を用いた式で捉え説明すること
(略…)
問題8:
解答: x=12.
解説: 3x+4+5x-2=100から、8x=98, x=98/8=12.25、しかし点数は整数なので12点。
指導要領の関連項目: 二元一次方程式の必要性と意味及びその解の意味
問題9:
解答: y=19.
解説: 2y-3+3y+2=100から、5y=101, y=101/5=20.2、しかし点数は整数なので20点。
指導要領の関連項目: 二元一次方程式の必要性と意味及びその解の意味
問題10:
解答: x=y.
解説: 新人とベテランの人数をx人、y人とすると、年齢の合計は20x + 30y、人数はx+y。これらの平均が25歳なので、(20x + 30y) / (x + y) = 25、これを解くとx=y。
指導要領の関連項目: 連立方程式を解くこと
数学の問題とはそれっぽいですが、解答が間違えていることがあるのでこの問題を必ず確認する必要があります。
やはり間違いが見つかった
確認してみると、問題8に間違いがありました。
問題8
ある数学の試験で、山田君と田中君の2人が全問正解しました。山田君の得点は3x + 4で、田中君の得点は5x - 2です。試験の満点は100点です。xの値を求めなさい。
上記の問題には間違いがあり、これだけではxの値を求めることはできません。下記が解説ですが、試験の満点が100点だったとしても、山田君と田中君の得点が100点というルールはありません。
3x+4+5x-2=100
このように数学の問題は正しいこともありますが、外れていることもあります。そのためには、叩き台の問題をChatGPTに作らせた後に確認が必要です。なので、問題文の叩き叩き台としては良いかもしれませんが、必ず検証が必要です。
ChatGPT-4とCode Interpreterで数学の問題作成
検証の結果、問題の解答が間違っていることが判明しました。これを、一つ一つの問題の解答を検証するのは時間がかかります。そこで、AIとコーディングを組み合わせて解答の検証を自動化することができます。
今度は、Code Interpreterを組み合わせて、プログラムを使って解答の検証まで行いたいと思います。実行順序を下記のように指定しました。
問題を作成
解答と指導要領の関連項目を作成
全問題のプログラムを作成して実行し、解答が合っているのかを確認
解答が合っていない箇所は解答を更新
解説を作成
実際のプロンプトは下記の通りです。
あなたは中学校の先生です。下記に指導要領があるので、それを参考に問題を10問作成してください。
そして作成された10問の問題を解くためのプログラムを作成して実行し、解答のチェックをしてください。
# 対象者
中学校2年生
# 科目
数学
# ルール
問題は後半の問題ほど難易度が上がる構成
最初の3問が選択式の問題
4〜10問目が自分で解答を記入する方式
最後の3問は文章題
# 指導要領
文字を用いた式の四則計算
・簡単な整式の加減及び単項式の乗除の計算
・文字を用いた式で表したり読み取ったりすること
・文字を用いた式で捉え説明すること
・目的に応じた式変形
連立二元一次方程式
・二元一次方程式の必要性と意味及びその解の意味
・連立方程式とその解の意味
・連立方程式を解くこと
# 出力
問題:
解答:
解説:
指導要領の関連項目:
# 実行順序
1 問題を作成
2 解答と指導要領の関連項目を作成
3 全問題のプログラムを作成して実行し、解答が合っているのかを確認
4 解答が合っていない箇所は解答を更新
5 解説を作成その結果は、下記のようになりました。10問作成されたのですが、一部の問題のみ抽出します。


その後、Code Interpreterの検証が開始され、Pythonのプログラムの生成と実行が行われます。
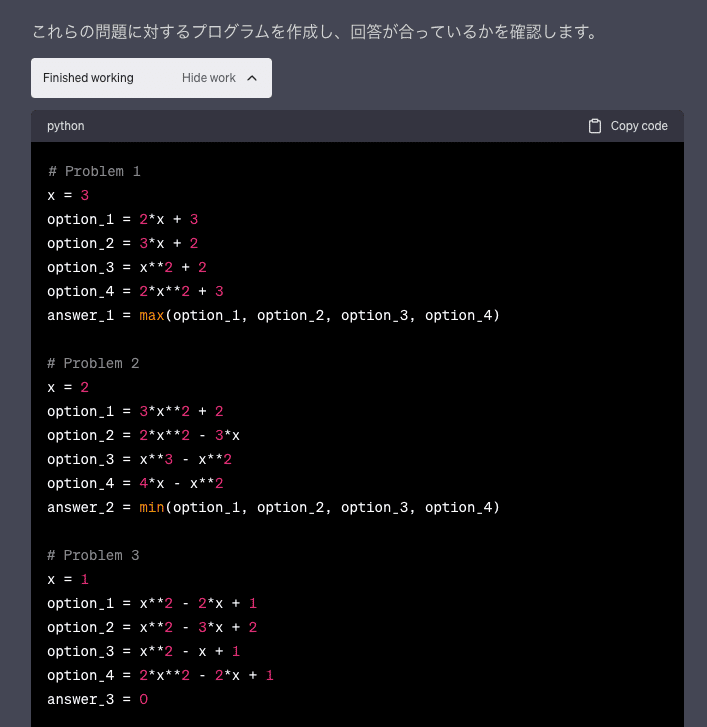
すると、下記のように問題が3問解答が間違えていると指摘してくれました。

更新後の解答は下記の通りです。

生成AIを活用して問題作成から検証まで自動化
AIはプログラミングの知識を持っており、Code Interpreterから問題の解答を自動的に検証するPythonのプログラムを作成することができます。これにより、教育者は時間を節約し、より効率的に問題作成とその検証を行うことができます。
この記事では、AIが問題作成から解答の検証までを一貫して行うプロセスを紹介しました。このような技術の進歩は、教育者がより質の高い教材を効率的に作成するための可能性を広げています。
しかし、AIはあくまでツールであり、その最終的な目的は教育者と学習者がより良い教育結果を出すことを支援することです。今後もこの視点を忘れず、AIを教育の現場で適切に活用していくことが重要となります。
教育者の方々にとって、この記事が新たな視点を提供し、教材作成の効率化や質の向上につながる一助となれば幸いです。
