論文メモ : A Watermark for Large Language Models
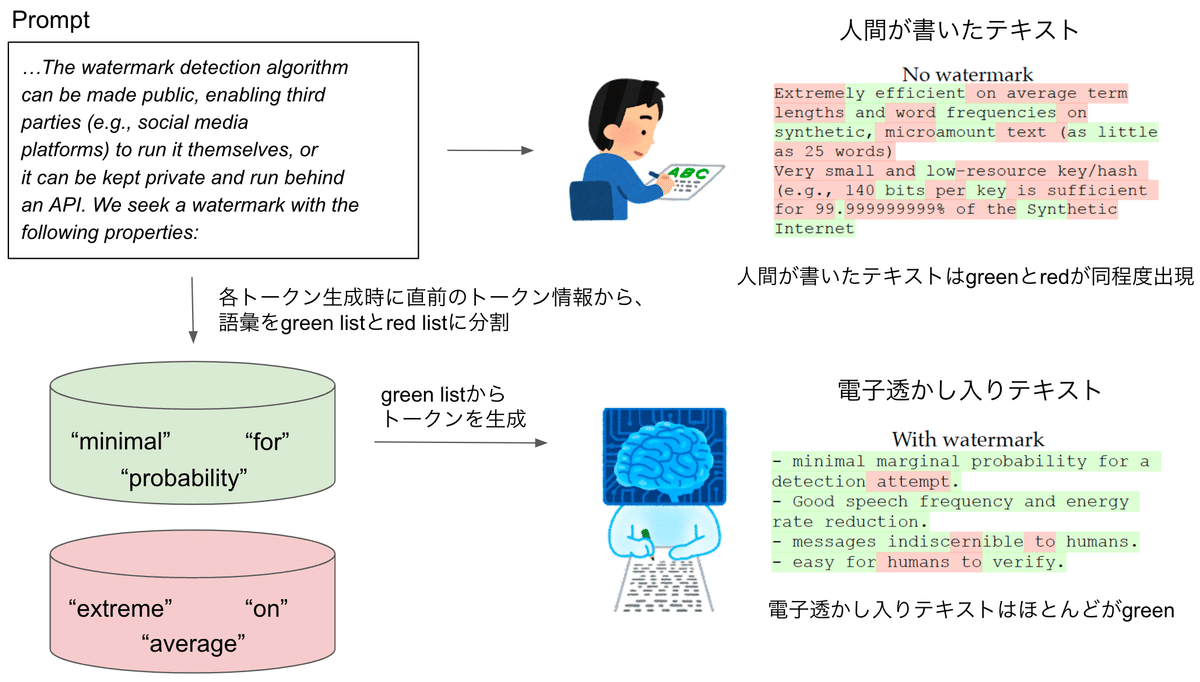
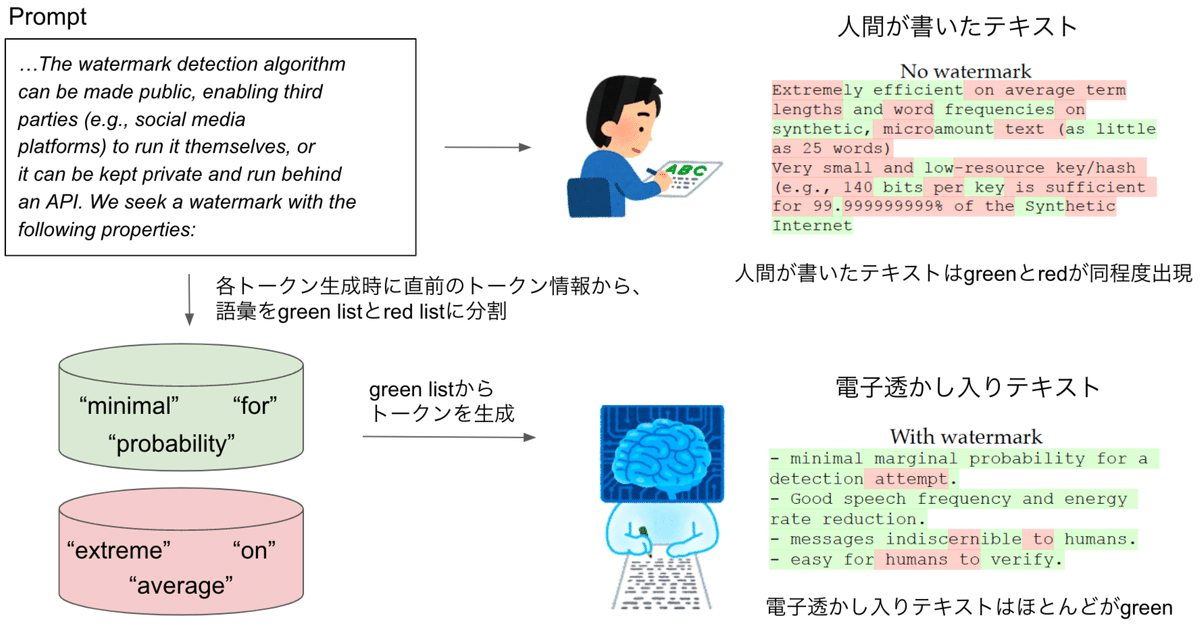
これまでの入力から次の単語を生成する際に、直前のトークン情報から、サンプリング候補とする単語リスト(green list)と候補としない単語リスト(red list)に分割して、green listから生成するように促す。
電子透かし入りテキストはgreenばかりになり、人間が書いたテキストはgreen listやred listなど認知していないので確率的に同程度のgreenとredの単語が出現する。
green が多い → 電子透かし入り と判断できる。
概要
テキストの品質にほとんど影響を与えることなく埋め込むことができ、言語モデルのAPIやパラメータにアクセスすることなく、効率的なオープンソースアルゴリズムを用いて検出することができる電子透かしフレームワークの提案。
この電子透かしは、単語が生成される前にgreenのトークンをランダムに選択し、サンプリング中にgreenのトークンの使用を促進することで機能。
解釈可能なp値を持つ電子透かしを検出するための統計的テストを提案し、電子透かしの感度を分析するための情報理論的枠組みを導出。
OPT(Open Pretrained Transformer)ファミリーの数十億パラメータモデルを用いて電子透かしをテストし、ロバスト性とセキュリティについて議論。
1. 導入
機械が生成したテキストの使用を検出して監査する能力は、大規模言語モデルの危害軽減の重要な原則
ソーシャルメディア・プラットフォーム上の自動ボットを悪用したソーシャル・エンジニアリングや選挙操作キャンペーン、フェイクニュースやウェブコンテンツの作成、学術的な論文執筆やコーディング課題の不正行為へのAIシステムの利用など。
ウェブ上の合成データの急増は、今後のデータセット作成の取り組みを複雑にしている。合成データは人間のコンテンツよりも劣ることが多く、モデル学習の前に検出し、除外しなければならない。
合成テキストを短いトークンのスパン(25トークン程度)から検出可能にする効率的な電子透かしを提案。
電子透かし検出アルゴリズムは、第三者(ソーシャルメディアプラットフォームなど)が自ら実行できるように公開することもできるし、非公開にしてAPIの後ろで実行することもできる。
本提案の特徴
モデルのパラメータを知らなくても、言語モデルのAPIにアクセスしなくても、アルゴリズムで検出することができる。
モデルがオープンソースでなくても、検出アルゴリズムをオープンソースにすることができる。また、LLMをロードしたり実行したりする必要がないため、安価で高速な検出が可能になる。
透かし入りテキストは、再トレーニングすることなく、標準的な言語モデルを使用して生成することができる。
電子透かしは、生成されたテキストの連続部分のみから検出可能である。こうすることで、生成されたテキストの一部分だけがより大きなドキュメントを作成するために使用されても、透かしは検出可能なまま。
生成されたトークンのかなりの部分を変更しない限り、透かしを除去することはできない。
電子透かしが検出されたという信頼性の厳密な統計的尺度を計算することができる。
1.1 Notation & 言語モデルの基礎
promptとpromptに対するAIの生成テキストを連結して系列とする
prompt : 負のindex
$${s^{(-N_{p})}, …, s^{(-1)}}$$
promptに対するAIの生成テキスト : 正のindex
$${s^{(0)}, …, s^{(T)}}$$
LLMのnext token predictionの説明。
$${-N_{p}}$$ から$${t-1}$$ 番目までのtokenから、$${t}$$番目のtokenを予測
入力から、ボキャブラリサイズのlogitsベクトルを出力。
ソフトマックス演算子に渡され、語彙の離散確率分布に変換。
多項サンプリング(multinominal sampling)や貪欲サンプリング(greedy sampling)などを使用して、位置tの次のトークンがこの分布からサンプリングされる。
1.2. 注意点:低エントロピー系列の電子透かし処理の難しさ
低エントロピーのテキストにおける電子透かしの2つの問題(低エントロピーのテキストでは電子透かしは困難)。
人間も機械も低エントロピーのプロンプトに対して、同じでないにしても似たような補完を行うため、両者を識別することが不可能。
トークンの選択を変更すると、高いperplexity、テキストの品質を低下させる予期しないトークンが生じる可能性がある。
2. シンプルな電子透かし、ハード電子透かし
アルゴリズム
分析が容易で、検出が容易で、除去が困難な “hard” red list watermark
低エントロピーのシーケンスでの生成品質が低いという代償あり

アルゴリズム1:
Input: サイズ$${N_p}$$のプロンプト
生成するテキストt = 0, 1, 2, …と逐次
$${s(-N_p)}$$から$${s(t-1)}$$のトークンに対して言語モデルを適用し、語彙サイズの確率ベクトル$${p(t)}$$を得る
トークン$${s(t-1)}$$のハッシュを計算し、それを乱数生成器のシードに使用する。
このシードを使って、語彙をランダムに同じサイズの”green list” $${G}$$と”red list” $${R}$$に分割する。
$${G}$$から$${s(t)}$$をサンプリングし、red listのトークンからは一切生成しない。
電子透かしの検出
透かし入りテキストの作成には言語モデルへのアクセスが必要だが、透かしの検出にはアクセスは必要ない。
ハッシュ関数と乱数生成器の知識を持つ者は、各トークンについてred listを再作成し、red listのルールに違反した回数を数えることができ、以下の帰無仮説を検証することで、電子透かしを検出することができる;
テキスト系列は、red listを全く知らない状態で生成される。
普通の書き手はred listを知らないので、red listからも$${1/2}$$の確率でトークンを生成する。red listのトークンを全く生成することなくT個のトークンを生成する確率は$${(1/2)^T}$$で限りなく小さい。これにより、LLMによる生成テキストを判別できる(LLMから生成されたテキストにはほとんどred listのトークンが存在しない)。
one proportion z-testによる帰無仮説の評価
green listのトークン数を $${|s|_G}$$ とし、$${T}$$個のトークンを生成するとすると、期待値 $${T/2}$$ 、分散 $${T/4}$$ で$${z}$$統計量は以下
$${z=2(|s|_G-T/2)/\sqrt{T}}$$
$${z>4}$$で帰無仮説を棄却するとすると、偽陽性(人間が生成したテキストをLLMが生成したと誤って推定してしまう)の確率は$${3\times10^{-5}}$$であり、これは$${z > 4}$$に対応する片側p値。
16個($${|s|_G=T}$$ のときに$${z=4}$$を生成する$${T}$$の最小値)以上のトークンを持つ任意の電子透かし系列を検出できる。
この電子透かしはどの程度除くのが難しいか?
本電子透かしを除くことは難しい。
長さ1000の本電子透かし付き系列を考える。
攻撃者が200個のトークンをred listのトークンに置き換え、電子透かしを除こうとしたとする。
200個のトークンをred listトークンに置き換えた場合、最悪の場合置き換えたトークンtの次のt+1のトークンもred listトークンに置き換わる場合でその場合最大で400トークンがgreen listトークンになる
この場合、残りの600トークンはgreen listのトークンとなり$${z}$$統計量は $${2(600−1000/2)/\sqrt{1000} ≈ 6.3}$$ で、p値は約 $${10^{-10}}$$ で、まだ非常に高い信頼度で電子透かしが検出可能。
一般的に、長いシーケンスの透かしを除去するには、トークンのおよそ4分の1以上を変更する必要がある。
上記の分析は、攻撃者が電子透かしの完全な知識を持っており、各選択されたトークンが最も攻撃的であるという前提。
電子透かしアルゴリズムの知識がない場合、変更された各トークンはred listにある可能性が50%しかなく、隣接するトークンも同様である。この場合、上記の攻撃者は、200のトークンを変更することで期待値として200のred listのトークンしか作成できない。 → 電子透かしを検出可能。
"hard" red list ルールの欠点
hard red listの欠点は、低エントロピーの系列においてそれら適切なトークンの生成を妨げてしまうこと。
トークン“Barack”の後には“Obama”がほぼ確定的に続くが、red listによって“Obama”は出力されないことがある
対策として、高エントロピーの系列においてのみアクティブになる”soft”な電子透かしルールを適用(セクション3で詳説)。
3. より賢い電子透かし、ソフト電子透かし
アルゴリズム
"soft" red list によるテキスト生成アルゴリズム

前提知識 : 言語モデルの最後の層はlogit $${l(t)}$$ のベクトルを出力し、これらlogitはsoftmax演算子によって確率ベクトル $${p(t)}$$ に変換される。
アルゴリズム 2:
Input :
サイズ$${N_p}$$のプロンプト
green listのサイズ比率 $${\gamma \in (0, 1)}$$
hardness parameter $${\delta > 0}$$
生成するテキストt = 0, 1, 2, …と逐次
$${s(-N_p)}$$から$${s(t-1)}$$のトークンに対して言語モデルを適用し、語彙サイズのlogitベクトル$${l(t)}$$を得る。
トークン$${s(t-1)}$$のハッシュを計算し、それを乱数生成器のシードに使用する。
このシードを使って、語彙をランダムにサイズ $${\gamma|V|}$$ の ”green list” $${G}$$とサイズ $${(1-\gamma)|V|}$$ の ”red list” $${R}$$に分割する。
green listトークンのlogitに定数 $${\delta>0}$$ を加えたlogitベクトルにsoftmax関数を適用し、語彙サイズの確率分布を得る。
トークン $${s(t)}$$を上記電子透かし分布(確率分布)を使いサンプリングする。
低エントロピーで”best”なトークンが明確な場合、そのトークンのlogit値は非常に大きくなり、red listにあるかないか関係なく確率値最大でありそのトークンがサンプリングされる。エントロピーが高い場合、$${\delta}$$ を加算したgreen listに高いlogit値が偏り、green listからサンプリングされやすい。
3.1 ソフト電子透かしの検出
hardの時と同様に、green listのトークン数を $${|s|_G}$$ 、$${T}$$個のトークンを生成するとし、任意の $${\gamma}$$ (green listのサイズ比率)に対して、ソフト電子透かしにおける$${z}$$統計量は以下
$${z=(|s|_G-\gamma{T})/\sqrt{T\gamma{(1-\gamma)}}}$$
hard watermarkと同様、$${z>4}$$で帰無仮説を棄却するとすると、偽陽性(人間が生成したテキストをLLMが生成したと誤って推定してしまう)の確率は$${3\times10^{-5}}$$であり、これは$${z > 4}$$に対応する片側p値。
ハード電子透かしの場合、テキストの特性に関係なく、16トークン以上の長さがあれば透かしの有無を検出できる。ソフト電子透かしの場合、検出能力はシーケンスのエントロピーに依存する。高エントロピーのシーケンスは比較的少ないトークンで検出されるが、低エントロピーのシーケンスは検出のためにより多くのトークンを必要とする。以下では、ソフト電子透かしの検出感度とそのエントロピー依存性を厳密に分析。
4. ソフト電子透かしの分析
電子透かし言語モデルによって使用されるgreen listトークンの期待値とエントロピーの関係を分析。
想定 : red listは一様にランダムサンプリングされるものとする
これは、過去のトークンをシードとした擬似乱数生成器を用いてレッドリストを生成する、実際に使用されている方法からは逸脱する。
擬似乱数サンプリングの結果はセクション5で検討。
テキストが多項ランダムサンプリングによって生成される場合を分析。実験では、さらに2つのサンプリング方式、貪欲な復号化とビームサーチを検討。
本電子透かしの強度は、トークン上の分布が1つまたはいくつかのトークンに集中した大きな「スパイク」を持つ場合に弱くなる。この現象を定量化するために次のようなエントロピーを定義。
定義4.1 スパイクエントロピーの定義
離散確率ベクトル $${p}$$ とスカラー $${z}$$ ($${z}$$検定量?)において、係数 $${z}$$ を持つ $${p}$$ のspike entropyを以下のように定義
$${S(p, z)=\sum\limits_{k}\frac{p_k}{1+zp_k}}$$
古典的なShannon entropyと同様、確率分布がどの程度広がっているかの尺度
spike entropyの最小値と最大値:
最小値 : $${p}$$ の全質量が一箇所に集中している場合。$${\frac{1}{1+z}}$$。
最大値 : $${p}$$ の質量が均等に分布している場合。$${\frac{N}{N+z}}$$。
大きな $z$ の場合の振る舞い
$${p_k>\frac{1}{z}}$$ のとき、$${\frac{p_k}{1+zp_k}\approx \frac{1}{z}}$$
$${p_k<\frac{1}{z}}$$ のとき、$${\frac{p_k}{1+zp_k}\approx0}$$
spike entropyは $${1/z}$$より値が大きい$${p}$$の数のsoftな指標と解釈できる。
定理4.2 透かしを含む系列に現れるgreen listのトークン数を予測する定理
$${T}$$ 個のトークンからなる電子透かし入りテキスト系列群を考える。
それぞれの系列は以下の流れで生成される:
言語モデルから確率ベクトル $${p^{(t)}}$$ を順次サンプリングし、サイズ $${\gamma N}$$ のランダムgreen listをサンプリングし、green listのlogitに $${\delta}$$ を加算したのち各トークンをサンプリング
$${\alpha=\exp(\delta)}$$ と定義し、$${|s|_G}$$ を系列 $${s}$$ 内のgreen listのトークン数とする。
ランダムに生成した電子透かし入り系列が少なくとも $${S^*}$$ の平均spike entropyをもつ場合、つまり、
$${\frac{1}{T}\sum\limits_{k}S(p^{(t)}, \frac{(1-\gamma)(\alpha-1)}{1+(\alpha-1)\gamma})\geq S^*}$$
の場合、系列内のgreen listのトークン数の期待値は少なくとも、
$${\mathbb{E}|s|_G\geq\frac{\gamma\alpha T}{1+(\alpha-1)\gamma}S^*}$$
さらに、green listのトークン数は最大で以下の分散となる。
$${Var|s|_G\leq T\frac{\gamma\alpha S^*}{1+(\alpha-1)\gamma}(1-\frac{\gamma\alpha S^*}{1+(\alpha-1)\gamma})}$$
$${\gamma \geq 0.5}$$ とすると、厳密性は弱いがよりシンプルには以下のように書ける。
$${Var|s|_G\leq T\gamma(1-\gamma)}$$
$${\gamma=\frac{1}{2}}$$ (green listのサイズ比率)、$${\delta=\ln(2)\approx0.7}$$(hardness parameter, green listのlogitに加算する値)とすると、期待値と分散の境界は以下のようにシンプルに書ける
$${\mathbb{E}|s|_G\geq\frac{2}{3}TS^*, Var|s|_G\leq\frac{2}{3}TS^*(1-\frac{2}{3}S^*)}$$
ここで、$${S^*}$$ は modulus(z検定量のことと推測)$${\frac{1}{3}}$$ でのspike entropyの上限。
“hard” red listについて、$${\gamma=\frac{1}{2}}$$ (green listのサイズ比率)、$${\delta \to \infty}$$(hardness parameter, green listのlogitに加算する値)とすると、期待値と分散の境界は以下
$${\mathbb{E}|s|_G\geq TS^*, Var|s|_G\leq TS^*(1-S^*)}$$
ここで、$${S^*}$$ は modulus(z検定量のことと推測)1 でのspike entropyの上限。
4.1 電子透かしテストの感度
type-II(偽陽性)エラー分析によるソフト電子透かし感度を理論的計算と経験的分析で実施。
$${\gamma=\frac{1}{2}}$$ (green listのサイズ比率)、$${\delta=2}$$(hardness parameter, green listのlogitに加算する値)におけるソフト電子透かしのtype-II(偽陰性, 電子透かし入りテキストを誤って電子透かしなしと推定する)エラーレート。
想定
OPT-1.3Bモデルで、C4データセットのRealNewsLikeサブセットからプロンプトを使用し、200トークンを生成。
検出閾値(z検定量)を $${z=4}$$ とし、この時のtype-Iエラー(偽陽性, 電子透かしなしのテキストを誤って電子透かしありと推定する)レートは $${3\times10^{-5}}$$。
理論的境界
500回のテキスト生成でspike entropyの平均は $${S = 0.807}$$
定理4.2 に基づくと、各生成におけるgreen listトークンの期待値は少なくとも142.2(200トークン中)。
実際の実験データでは、この平均は159.5。
spike entropyが$${S=0.807}$$のテキストは、標準偏差$${\sigma}$$は6.41トークン以下であり、98.6%の感度(1.4%のtype-II 偽陰性エラー率)(green listのサイズに対する標準的なガウス近似を使用)。
これは特定のエントロピーにおける感度の下界であることに注意。理論的平均値ではなく、経験的平均値の159.5を使用すると、type-IIエラー率は $${5\times10^{-7}}$$。
経験的感度
多項サンプリングを利用した場合、$${z=4}$$の閾値で98.4%の電子透かしが検出される。
ビーム幅4のビームサーチで探索した場合、99.6%の経験的感度(0.6%の偽陰性エラー率)。
type-II(偽陰性)エラーの主な原因は低エントロピーの系列。エントロピーが平均値の近くにある場合、上記の通り非常に低いエラー率となることが期待できる。
25 percentile以上のspike entropyを持つ375/500の生成物を調査したところ、$${z=4}$$の閾値で電子透かしの検出が100%の精度だった。
失敗例はどのようなものか?
電子透かしの典型的な成功例と失敗例(Table 1)

上段(成功例)
出力品質の知覚できる劣化なしに、高いエントロピーとそれに対応する高いzスコアを出している。
下段(失敗例)
エントロピーが低く、ほぼ同じ系列を出力している。
4.2. 生成テキストの品質への影響
言語モデルによって生成される分布が一様(エントロピーが最大)な場合、green listのランダム性によってトークンが一様にサンプリングされ、perplexityは変化しない(生成テキストの品質は変わらない)。
言語モデルの生成が単一のトークンに集中する(エントロピー最小)の場合、ソフト透かしルールは効果がなく、これもperplexityに影響はない(生成テキストの品質は変わらない)。
中程度のエントロピーを持つトークンの場合、電子透かしはperplexityに影響を与える。
5. 電子透かしアルゴリズムをプライベートにする
上記の電子透かしアルゴリズムは公開する想定で設計されている。
プライベートモードで動作させる場合、アルゴリズムはランダムなキーを使用し、このキーは秘密に保持され、セキュアなAPIの背後にホストされる。
攻撃者がred listを生成するために使用されるキーを知らない場合、どのトークンがred listに含まれているかを知らないため、電子透かしを除去することが難しくなる。
ウォーターマークの存在をテストするためには、同じセキュアなAPIを使用する必要があり、このAPIが公開されている場合、攻撃者が元の系列をわずかに変更して何度もクエリを投げるのを防ぐためにアクセスを監視する必要がある。
6. 実験
OPT-1.3Bモデルを利用し、電子透かしの偽陽性と偽陰性エラーの発生率を測定。
データセットとプロンプト
C4データセットのRealNewsLikeサブセットからランダムにテキストを選択。
選択されたテキストの末尾から固定長のトークンをトリミングして”baseline completion”として扱う。
残りの前半のトークンをpromptとして使用。
“オラクル”言語モデルとしてOPT-2.7Bモデルを使用し、生成されたトークン列と人間のベースラインのpreplexityの計算を行う。
電子透かしの強度 vs テキスト品質

(Figure 2 左)z検定量とテキスト品質のトレードオフ。強力な電子透かしを作成すると、生成されるテキストが歪む可能性がある。
各パラメータ($${\gamma}$$ : green listのサイズ比率、$${\delta}$$ : hardness parameter, green listのlogitに加算する値)選択毎に、長さT=200前後のトークンの系列約500件に対するz検定量とPPLの関係。
$${\gamma=0.1}$$ のとき、パレート最適(他の選択肢を悪化させることなく一方の選択肢を改善できない状態 = 最適なバランス)
$${\gamma=0.1}$$ のとき、電子透かしの強度とテキスト品質が最適のバランスになっている。(斜めにほぼ一直線に薄い緑が並んでいることを言っている?)
ビームサーチによる電子透かし
(Figure 2 右)ビームサーチは電子透かしの強度向上と相性が良い。
テキストの品質を下げずに(PPLがあまり変化せずに)z検定量を大きくすることができる。
特にビーム幅8のビームサーチ。
電子透かしの強度 vs 生成するトークン数

理論的には、系列長$${T}$$が長くなるにつれて、電子透かしの偽陽性、偽陰性エラー率はゼロに収束する。
Figure 3は、系列長$${T}$$が2から200に変化するときの電子透かしの強度の変化。
(a) 多項サンプリング下における、z検定量のgreen listサイズ比率($${\gamma}$$)との関係。
(b) 多項サンプリング下における、z検定量のhardness parameter(green listのlogitに加算する値, $${\delta}$$)との関係。
(c) ビームサーチ(ビーム幅8)下における、z検定量のhardness parameter(green listのlogitに加算する値, $${\delta}$$)との関係。
(???) 高いgreen list率(”high green list ratios”)を達成する際のビームサーチの威力が見て取れる。中程度のバイアス $${\delta=2}$$ でさえ、35トークンという少ないトークン数でz検定量が5を超える結果。(…と言及されているが、(c)はgreen list率0.25固定の図に見えるが、これは”high green list ratios”なのか?)
多項サンプリングにおける性能と感度

偽陽性(FPR)はどの設定でも全く観察されなかった。

(a) : 多項サンプリング
(b) : ビームサーチ(ビーム幅8)
(c, d) : (a, b)を半対数軸でグラフ化したもの。
高い $${\delta}$$ 値(hardness parameter, green listのlogitに加算する値)であるほど、高い性能。ビームサーチの方が多項サンプリングよりも同じ設定でわずかに高い精度。
7. 電子透かしへの攻撃
電子透かしに対する代表的な攻撃手法を実装し、評価。
言語モデルを利用した置換
別の言語モデルを使用して、オリジナルの出力テキストの一部を書き換えることで電子透かしを取り除こうとする攻撃。
ブラックボックス攻撃(モデルの内部にアクセスできない状態での攻撃)を想定。
電子透かしアルゴリズムは公開されていない状態を想定。
攻撃者はgreen listトークンにアクセスできず、ランダムなインデックスでトークンを置換しテキストを変更する。このトークンの置き換えは、特定の単語置き換え予算εに達するまで行う。
攻撃者はこの予算内で、オリジナルの電子透かしテキストと意味的類似性を維持しつつ攻撃テキストを作成する。
攻撃における各スパンの置き換えは、数百万パラメータを持つ言語モデルを使用して推論を行うことで実行される。
実験では、T5-Largeモデルを使用し、本攻撃を検証。
T5による置換攻撃の詳細
実験フロー
T5トークナイザを使用し、電子透かし入りテキストをtokneizeする。
εT回以下の成功した置き換えが行われるか、または最大のイテレーション回数に到達するまで以下の手順を繰り返す。
トークン化されたテキストの単語をランダムに選び、それを <mask> トークンに置き換える。
<mask> トークンの周囲のテキスト領域をT5に渡し、50-way beam searchを通してk = 20の候補となる置き換えトークンのシーケンスを取得。
それぞれの候補は文字列にデコードされる。モデルが返すk個の候補のうち、一つが元々のマスクされた領域に対応する文字列と異なる場合、攻撃が成功とみなされ、その領域は新しいテキストに置き換えられる。

↑(εが大きくなるにつれて攻撃 w/attack によってかなりTPRが下がり、FNRが上がっているように見える。論文中言及なし)

ε=0.1では、AUCの減少は0.01程度。
ε=0.3という大きな予算での電子透かしの削除はかなり成功しているが、攻撃されたシーケンスの平均PPL(Perplexity)は3倍に増加(テキストの質の悪化)し、さらに多くのモデル呼び出しが必要となる。
8. 関連研究
一部を簡単に取り上げ。
構文木や同義語テーブルに基づく、ルールベースによる透かし埋め込み(2000年代)
強力な透かしを入れようとすると、当時の言語モデルの柔軟性の限界によりテキストの品質を大幅に低下させた。
2022年にAaronsonはOpenAIと協力して、電子透かしに対する暗号技術のアプローチを研究していると発表。詳細は非公開だが、n-gramシーケンスのハッシングが関与していることを示唆する説明がある。
post-hocに検出するアプローチもさまざまあるが、言語モデルの能力が向上するにつれて困難になってきている。
詳細追えていないが、直近(7/28)で公開された電子透かしに関する論文
既存研究の課題の一つとして(今回紹介した論文が挙げられている)、モデルのサンプリング分布を歪めてしまうが、本手法はサンプリング分布を歪めない

LM ProviderとDetectorで ”共有鍵” を持ち、テキスト中のどこがLM Providerによって生成されたものか検出する。以下プロトコル↓
ユーザーがLM Providerにプロンプトを送信
LM Providerがユーザーに電子透かし入りテキストを送信する
ユーザーが検出を回避するために電子透かし入りテキストを編集し、公開する
DetectorはLM Providerとの共有鍵を利用して、公開されたテキストのどこがLM Providerが生成したものか検証する
9. 結論
提案手法の重要な性質
検出に使用されるz検定量が、green listのサイズパラメータ$${\gamma}$$とハッシュ関数のみに依存している点。
異なる種類のテキスト(例えば、文章とコード)に、コンテキスト固有の$${\delta}$$やgreen listのルールを使用して電子透かしを適用することができる。そして、それに対する検出器は同じものを使用できる点。
電子透かし付きのサンプリングアルゴリズムの実装を変更しても、検出器を変更する必要はない点。
特定のユーザーが疑わしい行動を示す場合など、特定の状況でのみウォーターマークを有効にすることができる点。
今後の課題
電子透かしをどのようにしてストリーミングのコンテキストでテストするか。
電子透かし入りのテキストスパンが、非電子透かしの長いスパン内に短い長さで存在するコンテキストでどのようにテストするか。
Appendix(B.1. 電子透かしへの攻撃手法)
電子透かしへの攻撃パートを取り上げ。
Paraphrasing Attacks
ベースラインの置換攻撃は、人間の攻撃者による手作業での言い換え攻撃。
この攻撃は、広範囲に及ぶ人間の介入を必要とするため、技術的には私たちが興味を持っている脅威モデルの範囲外。
自動化された言い換えはセクション7.1で議論した、別の言語モデルを利用しての書き換え。
Discreet Alterations
空白を追加したり、単語のスペルを間違えさせたりする攻撃。
この方法は、テキストの品質を著しく低下させる可能性が高く、電子透かしに深刻な脅威をもたらすことはない。
Tokenization Attacks
入力テキストを変更することで、後続の単語のサブワードトークン化を変更させる攻撃。
例 : “life. \\nVerrilius” というテキストが “life. Verrilius” と変更される(”\\n”が置換される)と、BPEではVerriliusのトークン化が”V_err_ili_us”から”Ver_r_ili_us”に変更される。
これにより、red listトークンの挿入率が上がる。
ほとんどのトークンはこのような脆弱性はないのでそれほど脅威にはならない。
Homoglyph and Zero-Width Attacks
ホモグリフ攻撃による、非常によく似ているがユニコードIDの異なる文字への置き換えにより、上記Tokenization Attackのようにトークン化が変更される。
例 : “Lighthouse” という単語(通常2トークン)は、”i” と “s” をキリル文字(表記上は等価だがユニコードIDは異なる)に置き換えると、9トークンになる。
ゼロ幅のユニコード文字の挿入も影響を受ける。
対策として、入力テキストの正規化処理を入れる必要がある。
Generative Attacks
In-context learningを悪用し、テキスト生成時にルールに沿って特定の文字を挿入した上でテキスト生成をさせる攻撃。

(Figure 6 左) トークンごとに絵文字を生成するよう指示しモデルにテキストを生成させる。これにより後続のred listが意味をなさないものになる。攻撃者は絵文字を後処理で除けば、自然なテキストが得られる。
(Figure 6 右) テキスト生成時に “n” を “m” に、”a” と “e” に置換して生成するように指示する。
この攻撃は著者の知る限り、最も強力な攻撃手段
だが、出力品質を落とさずに上記指示に従うことのできる言語モデルを用意する必要があるのと、通常よりも多くのトークンを生成する必要があるため生成コストが大きい。
対策としては、このような要求を拒否するようにモデルを訓練すること。
この記事が気に入ったらサポートをしてみませんか?
