
Welzlの最小球アルゴリズムを非再帰で実装する
前回Welzlの最小球アルゴリズムの理屈を説明しました:
最終的なアルゴリズムはシンプルなのですが、非常に激しい再帰呼び出しが起こる為、点群の数が増えるとすぐにスタックオーバーフローを起こしてしまいます。よってこのアルゴリズムを実用するには再帰しない形に直さないとちょっと実用に耐えないんですね。
そこで今回は非再帰なWelzlアルゴリズを実装してみようと思います。
単純にスタックするのは無理がある
関数が呼び出される時に引数と関数内のローカル変数がスタックメモリに積まれます。再帰関数でもそれは同様で、再帰関数が内部で呼ばれるたびにそれらがスタックに積まれ続ける事になります。そのスタックメモリが通常数十MBしかないため、巨大な引数やローカル変数を確保するとあっと言う間にスタックオーバーフローを起こしてしまうわけです。
再帰関数を非再帰化する場合には、スタックメモリに積まれる物をヒープメモリに置いて自前でプッシュ&ポップするのがセオリーです。しかし今回のb_miniSphere関数の引数は共に点群リストであるため、無計画にそれをするととんでもないメモリ領域を消費してしまいます。メモリ効率的にも動作効率的にも流石にそれはまずい…。これは別の方針を考えないと埒が明かなかそうです。
点群Pから1点を除く=リストのインデックスを下げる
b_miniSphere関数は、最初に引数の点群Pから1点を取り除きます。これは関数の内部だけの一時的な処理で、関数を抜けて上位のb_miniSphere関数に戻ると、点群Pは取り除く前のリストに戻ります。b_miniSphere関数が呼ばれるたびに1点少ない点群Pになっていき、戻る度に除いた1点が復活していく。これは非再帰関数版では「リストのインデックスを下げる」ことで表現できそうです:
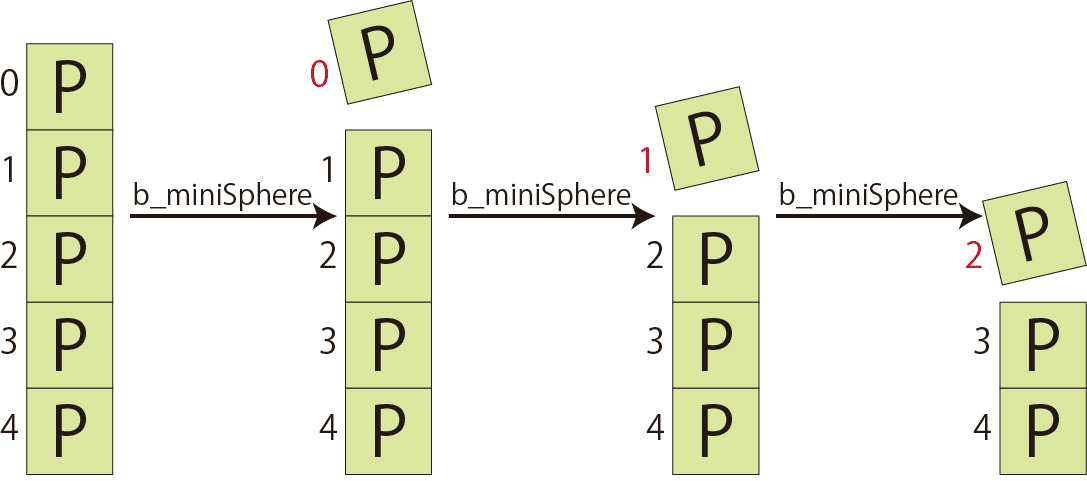
上図のようにb_miniSphereが呼ばれる個所でリストのインデックスを一つ下げて(インクリメントして)そのインデックスより下の点群を残りと捉えれば良いんです。逆にb_miniSphereから戻るreturnの個所でインデックスを一つ戻せば上位のb_miniSphere関数の状態に回復します。つまり非正規関数内に呼び出しの深さを表す変数を保持しておけば良く、点群Pは参照するだけでOKと言う事になります。点群Pの扱いはこれで良さそうです。
円周上の点群Rは追加した後のreturnで戻る
次にもう一つの引数、最小円の上にある点群Rについて考えてみます。点群Rが変化するのはb_miniSphere関数の中盤、1点除いた点群P'を包む暫定的な最小円(球)が返って来て、その円に除いた点が含まれていない場合です。その場合のみ点群Rに除いた点が追加され、b_miniSphere関数に再び引き渡されます。そしてそのb_miniSphere関数から戻ったらそのままreturnとなり、さらに上位のb_miniSphere関数に戻ります。追加していた点はそのタイミングで取り除かれる事になります:

この事から点群Rについては要素数3(3Dの場合は4)の配列を用意しておいて、有効な要素数(RNum)を上げ下げすれば良さそうです。点群Rもスタックに積む必要は無いんですね。
呼び出しの深さ毎の状態は必要
非再帰化では一般にwhile文などのループで関数呼び出しを模倣します。ループの中で深さ変数が増えれば一段深いb_miniSphere関数が呼ばれた事になります。
Welzlのアルゴリズムではb_miniSphere関数は内部で2か所b_miniSphere関数を再帰的に呼び出しています。一つは最初の1点を取り除いた直後、もう一つは取り除いた点が最小円に含まれていなかった時です。呼出しからreturnした時、どちらの関数が呼び出されたか分からないと処理を正しく継続できません。そしてこれは深さ毎に状態があるので、深さ=点群の数分だけバッファーが必要になります。
具体的に、1つの深さに対して次の3つの状態保持が必要になります:
Remove(1点取り除いた直後)
Compare(最小円が返ってきた後、除去点との比較)
Return(除去点が最小円外だった時の2回目の再帰状態)
最初の点群Pが100点あるとしたら、100段分の状態保持が必要です。と言っても上の3状態のみなので、非再帰化関数の最初で1バイト(char型)×点群数の状態保持用の配列を用意しておけばOK。
暫定的な最小円(球)は一つでOK
m_miniSphere関数は最小円(球)を返します。これは点群Pが空の時に点群Rから計算されて戻される物です。戻ってきた最小円は除去点との比較に利用され、最小円内に点があればそのままreturn、無ければ一段下がって再計算されます。この事から最小円は1つだけ情報を保持しておけばよく、スタックする必要はありません。
非再帰化b_miniSphere関数の実装
それでは以上の前情報を元に非再帰化なb_miniSphere関数を疑似コードで実装してみましょう。ただいきなり完成形を見ても混乱しかしないと思いますので(^-^;、少しずつコードを追加していきます。
関数の引数は対象となる点群Pのみです。そして点群Pを囲う最小円(球)を返します:
Sphere b_miniSphere( List P ) {
...
return sphere;
}関数内で使うローカル変数は、
現在の深さ(=除去点のインデックス)
点群Rの配列(2Dなら要素3、3Dなら要素4)
点群Rの登録数
深さ毎の状態配列(要素数は点群Pの点の数)
暫定最小円(球)
です:
Sphere b_miniSphere( List P ) {
int i = 0; // 除去点インデックス(=深さ)
List R(3); // 点群R(3Dなら要素数4)
int RNum = 0; // 点群Rの登録数
List states( P.size() ); // 状態配列(Removeで初期化:ヒープから確保)
Sphere sphere; // 暫定最小円(球)
...
return sphere;
}非再帰化なので関数内でループし続けて再帰と同様の処理をしていきます:
Sphere b_miniSphere( List P ) {
int i = 0; // 除去点インデックス(=深さ)
List R(3); // 点群R(3Dなら4)
int RNum = 0; // 点群Rの登録数
List states( P.size() ); // 状態配列(Removeで初期化:ヒープから確保)
Sphere sphere; // 暫定最小円(球)
while( i >= 0 ) {
...
}
return sphere;
}ループの終了条件は除去点のインデックスが完全に元に戻って振り切るまでです。深い所からreturn、returnで戻り続けて一番最初の関数からreturnする時、深さは-1になるわけですね。
ループ内の最初では具体的な最小円を算出します。算出の判断は点群Pが空になっている場合、つまり除去点のインデックスが点群数に達した時です:
Sphere b_miniSphere( List P ) {
int i = 0; // 除去点インデックス(=深さ)
List R(3); // 点群R(3Dなら4)
int RNum = 0;
List states( P.size() ); // 状態配列(Removeで初期化:ヒープから確保)
Sphere sphere; // 暫定最小円(球)
while( i >= 0 ) {
if ( i >= P.size() ) {
sphere = calcMiniSphere( R, RNum );
i--;
}
...
}
return sphere;
}点群Rの情報を元に対応する最小円(球)を算出したら、再帰版の場合はすぐにreturnが走ります。つまり深さが一つ戻るのでiをデクリメントしています。
続けましょう。最小円の計算をしない場合、点群Pから一つ点を取り除き、すぐにm_miniSphreを呼び出していました。これはi番目の点に対する状態がRemoveの時の処理となります:
Sphere b_miniSphere( List P ) {
int i = 0; // 除去点インデックス(=深さ)
List R(3); // 点群R(3Dなら4)
int RNum = 0;
List states( P.size() ); // 状態配列(Removeで初期化:ヒープから確保)
Sphere sphere; // 暫定最小円(球)
while( i >= 0 ) {
if ( i >= P.size() ) {
sphere = calcMiniSphere( R, RNum );
i--;
}
else if ( states[ i ] == Remove ) {
// 一段下がる
states[ i ] = Compare; // 戻って来た時は比較状態のため
i++;
}
...
}
return sphere;
}一段深い所に移行するのでiをインクリメントしますが、現在のi番目の状態はRemoveからCompareに変わります。再帰の時はここで関数呼び出して戻ってきた後は最小円との比較フェーズになる為です。
続いて状態がCompare、最小円と除去点との比較の時は、円内に点があるか否かで遷移が変ります:
Sphere b_miniSphere( List P ) {
int i = 0; // 除去点インデックス(=深さ)
List R(3); // 点群R(3Dなら4)
int RNum = 0;
List states( P.size() ); // 状態配列(Removeで初期化:ヒープから確保)
Sphere sphere; // 暫定最小円(球)
while( i >= 0 ) {
if ( i >= P.size() ) {
sphere = calcMiniSphere( R, RNum );
i--;
}
else if ( states[ i ] == Remove ) {
// 一段下がる
states[ i ] = Compare; // 戻って来た時は比較状態のため
i++;
}
else if ( states[ i ] == Compare ) {
if ( sphere.contain( P[ i ] ) {
// 含んでいるので一段上がる
states[ i ] = Remove;
i--;
} else {
// 外にあるのでRに追加し一段下げる
states[ i ] = Return;
R[ RNum ] = P[ i ];
RNum++;
i++;
}
}
...
}
return sphere;
} 除去点が暫定最小円内にある場合はその円をそのまま採用して一段上に戻ります。よってiをデクリメントします。その際今の段数の状態はRemoveにリセットされます。再びこの深さになった時は点iを1点除去する所からになるためです。
除去点が円の外にある場合は点群Rに除去点を追加し、登録数RNumを一つ増やし、一段深い所に潜ります(iをインクリメント)。そして呼び出しから戻った後にRNumを減らす必要があるために状態をReturnにセットしておきます。
最後、その状態がReturnの時は点群Rの最後尾追加をポップするのでRNumを一つデクリメントします:
Sphere b_miniSphere( List P ) {
int i = 0; // 除去点インデックス(=深さ)
List R(3); // 点群R(3Dなら4)
int RNum = 0;
List states( P.size() ); // 状態配列(Removeで初期化:ヒープから確保)
Sphere sphere; // 暫定最小円(球)
while( i >= 0 ) {
if ( i >= P.size() ) {
sphere = calcMiniSphere( R, RNum );
i--;
}
else if ( states[ i ] == Remove ) {
// 一段下がる
states[ i ] = Compare; // 戻って来た時は比較状態のため
i++;
}
else if ( states[ i ] == Compare ) {
if ( sphere.contain( P[ i ] ) {
// 含んでいるので一段上がる
i--;
} else {
// 外にあるのでRに追加し一段下げる
states[ i ] = Return;
R[ RNum ] = P[ i ];
RNum++;
i++;
}
}
else if ( states[ i ] == Return ) {
// Rの登録数を戻し一段上がる
state[ i ] = Remove;
RNum--;
i--;
}
}
return sphere;
}一段上がるので現在の点iに対する処理の状態はRemoveにリセットです。
これでWelzlの最小円アルゴリズムを非再帰化できました!上の数十行の疑似コードをお使いの言語で書き下せば動くはずです。
今回のコードでは計算に必要なメモリを最初に全部確保しています。単発的な変数はローカル変数(スタックメモリ)に、唯一巨大な配列となるstates状態配列はヒープメモリから取っています。そのため途中でリストを伸長するなどのメモリ再確保のコストはありません。もちろん再帰的な関数呼び出しは無い為スタックメモリの追加消費もありません。扱う言語にもよりますが、例えば今時のPCでC++で書けば数十万点くらいは全く問題無く動作します。非再帰化のパワーを感じて頂けると思います。
ではまた(^-^)/
