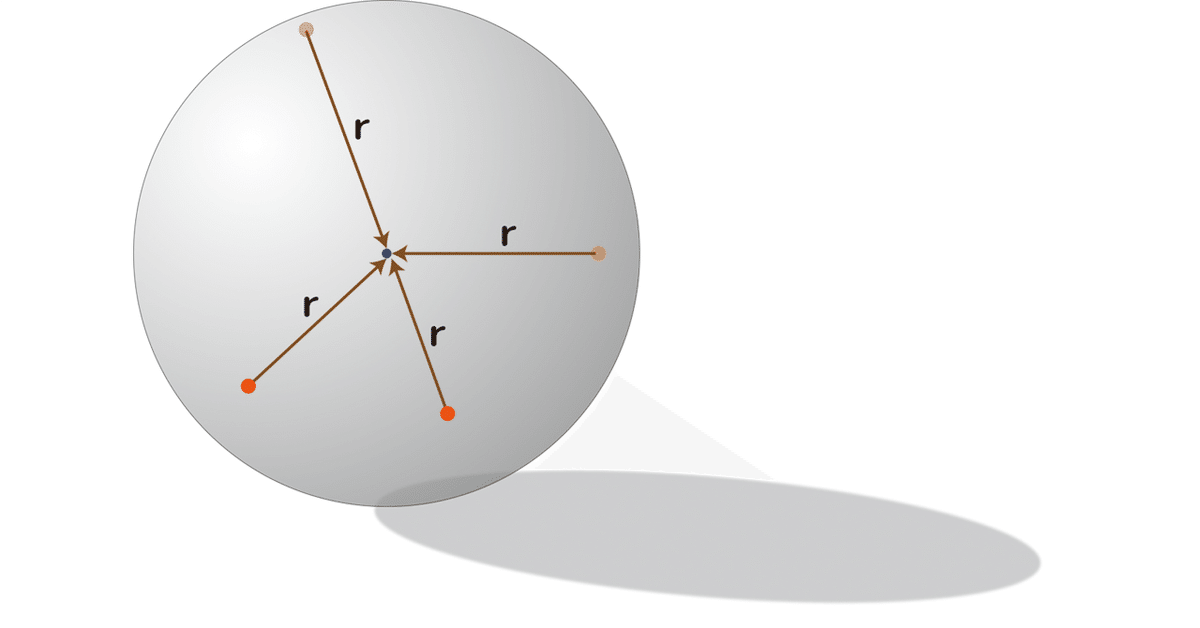
4点を通る球を求める

　3次元空間に球を定義する時、普通は中心点の座標と半径を設定します。ただゲームプログラムや3Dメッシュを扱うコードを組んでいると、そうではなくて球が通る点の座標だけはわかっていて、そこから球の中心点と半径を逆算したい事もあります。

　3次元の球を決めるにはその表面に点が4つ必要です。なぜ4つかと言うと方程式の中に未知のパラメータが4つあるためです：

　上式で(x, y, z)は球面上の点の座標で、これは変数です。一方(cx, cy, cz)は球の中心座標、rは半径でどちらも係数（パラメータ）です。つまり上式は「球の中心点(cx, cy, cz)から等しい距離rにある点の集まり」を表しているんですね。そして未知係数が4つあるので、それらを定めるには連立方程式が4本必要。なので4点なんです。

　ただし注意。その4点の内3点が一直線上に並んでいてはいけません。また4点が同一平面上にあっても方程式は一意の解を持たなくなります。もちろん4点のどれかが重なっているのもNGです。以下はこの例外に無い4点である前提でお話を進めます。

2つの断面円の法線の交点が中心点

　球面上にある4点から3つ点を選び異なる三角形を2つ作ります。各頂点は球面上にあるので、その三角形を含む平面で球を部分的に切る事ができます：

　双方の三角形の平面で球を切り取るとその断面は円になります。その断面円の中心を通る法線上には球の中心点が必ず存在します。法線が1本だとどこにあるか分かりませんが、別方向の法線がもう一つあればその交点で球の中心点を見つけられます。

　よって必要なのは断面円の法線とその円の中心点です。法線は簡単。断面円に三角形が含まれているのですから、三角形の法線を求めれば良いだけです。一方中心点は上図からも分かるようにその三角形の外心です。3次元空間に浮いている三角形の外心を求めるには少し理屈が必要です。

3Dな三角形の外心（外接円の中心点）を求める

　下図をご覧下さい：

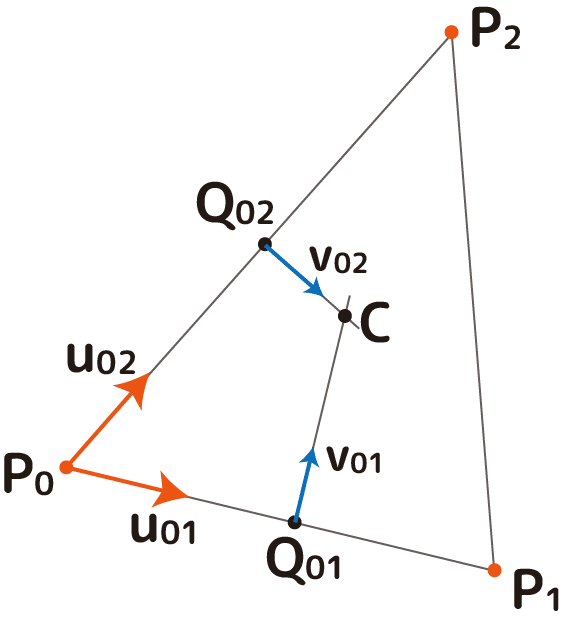
　この三角形は2D平面ではなくて3次元空間内に浮いているとします。その頂点をP0、P1、P2、P0からP1の方向に伸びるベクトルをu01、P2の方に伸びるのをベクトルu02とします。Q01とQ02はそれぞれその辺の中点で、青矢印のv01、v02はその辺に垂直で三角形の平面に沿うベクトルです。ここから外心はCになります。

　図から外心CはQ01-C、Q02-Cの直線の交点なので、2本の直線式を連立方程式で解いて共通点を求めれば良いわけです。この時、

このように2本の直線式を立てて媒介変数t1、t2を設けて…とやっても解けますが、よりうまい方法があります。

　まずQ01-Cの直線は陽関数で表現します：

a(t)は直線上の任意の点座標で、変数tは任意の数値です。Q01を起点としてベクトルv01をt倍した点は直線Q01-C上にある点になりますよね。よってa(t)=Cとなるtが存在するはずです。

　もう一つの直線Q02-Cは陽関数ではなくて陰関数で表現します。ここがこの方法のご機嫌な所です：

　図からわかるようにu02とv02は垂直関係ですよね。なのでその内積は0。式中のv02は括弧のようにQ02と中心点Cで表現し直せます。

　上式の陰関数で分かっていないのは外心点Cです。先程Q01側の直線式で、a(t)=Cになるtがあると言いました。という事は上式のCにa(t)を代入できるんですね。すなわち、

この式を満たすtが中心点Cに到達するtになるわけです。式中の内積は分配法則が成り立つので、普通の変数の掛け算のように展開していけます：

という事で外心Cに到達するtは上式を逐次的に計算すれば求まります。上式の分母はゼロになる可能性がありますが、それは三角形が縮退している時です。三角形がちゃんと平面を成していれば大丈夫です。

　この式内でv01以外は三角形の頂点からすぐに求まります。v01はu01に垂直なベクトルですが、今は2次元じゃなくて3次元で考えているのでu01と垂直なベクトルは無数にあるんですね。その中でv01はu01に垂直で且つ「平面の法線にも垂直（＝三角形平面に平行）」という2つの条件を満たしているものになります。

　u01と平面法線nの2つのベクトルに垂直なベクトル…というと、そうです、それは「外積」で求まるんですね。つまり、

です。

　平面法線はu01とu02に垂直なベクトルですから、

です。これで三角形の頂点の情報だけから中心点Cの座標を逐次計算で求められますね。

　ここまでの理屈で外積の掛ける順番とか大丈夫なのかなと思った方もいらっしゃるかもしれません。それは大丈夫です。外積の掛ける順によってベクトルv01の方向が反対になったりしますが、それは最終的に求まるtの符号が全部吸収してくれます。

2本の中心点を通る直線から球の中心点を求める

　ここまでで三角形の外心計算から切断面の中心点Cとその法線nが求まりました。2つの三角形T1とT2それぞれで外心C1、C2及びn1とn2を求めれば、球の中心を貫く直線を定義できます：

　ところで3次元空間で2つの直線が交わる…これ通常は非常に稀な事です。例えばプレゼンとかで使うレーザーポインタを2つ用意して、それを空中で交差させる事を想像するとそれがとても難しい事がイメージできますよね。ましてや太さが無い概念上の直線を交差させるなんて稀中の稀です。なので上の図から「2つの直線の衝突点を求める」という考え方はコンピュータ計算ではちょっとヤバいんです。浮動小数点の計算は誤差がつきまとうため、まともにやると交差判定してくれないんです。

　でもよく考えてみて下さい。上の直線C1-CsとC2-Csは「交差する事が数学的に分っている」非常にありがたい直線なんです。そう、交差はもはや前提です。交点を求めるのにその性質を使わない手はありません。

　まずC1-Csを陽関数で表現します：

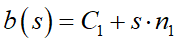
　この流れ、何だかデジャブを感じます。そうです、もう一方のC2-Csを陰関数で表現できれば、外心の時と全く同じ展開を使えるんですね。そのためにはベクトルn2と垂直なベクトルが必要です。それは上図のベクトルu2です。ベクトルn2は青い三角形の法線ですから、平面上にある2点を結んだベクトルならどれもn2と垂直になります。これで陰関数を、

と定義できます。外心の時と同様にb(s)をCsに代入して整理すると、

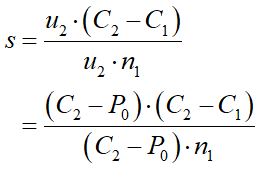
球の中心点に到達するsを求める式が出来ました！分母がゼロになるのはu2とn1が垂直関係にある時、つまり2つの三角形が平行関係にある、別の見方をすれば球面上の4頂点が1つの平面上にある場合です。勿論u2やn1がゼロベクトルの場合もそうです。いずれも縮退的な状態にある場合に起こります。

　中心点Csさえ求まれば半径rはCsと表面上の1点p0との距離ですから、計算は造作もない事です。

コードを書こう

　それではここまでの理屈を疑似コードに落としましょう：

// 4点を通る球を求める
bool calcSphereFrom4Point( Vector3 ps[4], Sphere &sphere ) {
   // 4点を2つの三角形に分ける
   Triangle t1( ps[0], ps[1], ps[2] );
   Triangle t2( ps[0], ps[1], ps[3] );

   // 三角形の外心を算出
   Vector3 n1, n2;
   Vector3 c1, c2;
   if ( !calcOuterCenter( t1, &c1, &n1 ) || !calcOuterCenter( t2, &c2, &n2 ) ) {
      return false;
   };

   // 球の中心点に到達するsを算出
   Vector3 u2 = c2 - ps[0];
   float denom = u2.dot( n1 );
   if ( denom == 0.0 ) {
      return false;
   }
   float s = u2.dot( c2 - c1 ) / denom;

   sphere.center = c1 + s * n1;
   sphere.radius = ( ps[ 0 ] - sphere.center ).length;

   return true;
}

// 三角形の外心と平面法線を求める
bool calcOuterCenter( Triangle t, Vector3 &c, Vector3 &n ) {
   Vector3 q01 = ( t.p[ 1 ] + t.p[ 0 ] ) * 0.5;
   Vector3 q02 = ( t.p[ 2 ] + t.p[ 0 ] ) * 0.5;
   Vector3 u01 = t.p[ 1 ] - t.p[ 0 ];
   Vector3 u02 = t.p[ 2 ] - t.p[ 0 ];
   n = u01.cross( u02 );
   Vector3 v01 = u01.cross( n );
   
   float denom = u02.dot( v01 );
   if ( denom == 0.0 )
      return false;

   float t = u02.dot( q02 - q01 ) / denom;
   c = q01 + t * v01;

   return true;
}
 
struct Sphere {
   float center;
   float radius;
}
 
struct Triangle {
   float p[3];
}

　実際に動くようにするには3成分のVectorや内積、外積、長さなどの基礎計算が必要になります。UnityのVector3なら全部揃ってますよね。C++などでそれらが無くても作るのは容易でしょう。SphereとTriangleはそのまんまの構造体です。Sphereには中心点centerと半径radiusが、Triangleは3点を表す配列pがそれぞれメンバにあります。

　関数内で例外的な点の並びによって起こる例外を検知しています。例外が起こる条件は、

• 4点が同一平面上にある

• 3点が直線上に並んでいる

• 少なくとも1つ以上の点が他と重なっている

これらのいずれかで、いずれも式中の分数の分母（denom）がゼロになります。

　という事で今回は球面上の4点から中心点と半径を求める理屈を見てきました。方程式を解かずに逐次的に計算できるのはお手軽ですよね。

ではまた(^-^)/