辺が凸っていく正方形の周の長さと面積(解説)
問題はこちら:
答え:面積は2、周の長さは無限大
問題の手順で辺を凸にしていった時、その面積は2に限りなく近づきます。一方で周の長さはどんどん伸び続け、無限の長さになってしまいます!有限の面積なのに周は無限という不思議な図形。なぜそうなるか解説します。
解説:無限等比数列の和がポイント
周の長さは無限大に
まずは周の長さを見ていく事にしましょう。
最初の一辺1の正方形の段階をn=1と表す事にします。以後各段階での辺の数をEn、1辺の長さをLnとします。すると周の長さAnはLnの長さがEn本あるので、

と双方の掛け算で計算できます。n=1の時は辺の数E1=4、1辺の長さL1=1なので、周の長さA1は、

ですね。
次に各辺を3等分して真ん中を凸。これにより1辺は5辺に増えます:

そしてn=1の時の正方形は右の図形になります:

この段階をn=2とします。E1=4の各辺が5つに増えるので辺の総数E2は5倍の20になります。つまり、

また各辺の長さL2はL1の1/3に短くなります。これも、

このように一つ前の長さを使って表現できます。ここからn=2の図形の周の長さA2は、

n=1の時の5/3倍に伸びるのがわかります。
n=3の時も見ておきましょうか。n=2の各辺が同様に凸になるので、辺の数E3は、

E2の5倍になり、そこから最初のE1の5²倍になるのもわかります。L3もL2の1/3に縮むので、

やはり2乗倍になります。ここまで来れば後は同じです。n=kの時はそれぞれ、

こうなりますので、n=kの時の周の長さAkは、
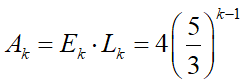
こういう一般式で表される事になります。この式は初項4、公比5/3の等比数列です。このkが∞まで吹っ飛ぶと公比が1より大きいのでAkは無限大に飛んでいきます:

つまり図形の辺の構造が微細になればなるほど、その周の長さは無限に長くなってしまうんです。
面積は収束する
さて一方の面積はどうなるか見て行きましょう。各段階で凸によって増えた小型の正方形の数をTn、辺の本数をEn、その1辺の長さをLnとします。
n=1の時、TnとLnはそれぞれ以下の通りです:

最初の正方形は凸になったわけではありませんが、無な所から凸になったと考える事にしましょう。ここからn=1での面積は、

となります。正方形ですから面積は辺Lのべき乗ですよね。E1が使われていませんが、これは次のn=2の所で出てきます。
次にn=2段目:

凸で出てきた大きさ1/3の正方形の数T2はn=1の時の辺の数と同じになるので、

であるのがわかります。辺の数E2と長さL2は周の時と同様で、
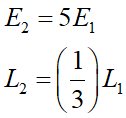
ここからn=2段階目の面積は、n=1の時の正方形とn=2で増えた分を合わせるので、

下段のような式になります。もう少し先も見てみましょうか。
n=3段目:

新規に凸った所は明るい緑の小さな正方形です。この数はn=2の時の辺の数E2に一致するので、

です。辺の数E3と長さL3はそれぞれ、

でしたね。ここから面積S3はS2を足す事に注意して、

こう展開されます。
式の法則性が見えましたでしょうか?括弧内はn=kの時に1/9のk-1乗と5のk-2乗が掛け算された値が追加される事になります。式で表すと、

このようになります。ここで括弧内の各項に5/5を掛けると、

初項5/9公比5/9の等比数列の和の形に整理できます。公式を知っている方はそれに放り込めば合計がでます。公式どうだっけ?という方(=自分ww)のために実際に計算してみます:

括弧内をAとします。Aに5/9を掛けて下段の式を作り、上から下を引くと、

このような一般式が導けます。このkを無限大に飛ばすと第2項は0に漸近しますから、

5/4になります。これをSkの式に代入すると、

無限段階続けた時に面積が2に漸近する事がわかりました。周の長さは無限大ですが、面積は2倍になるに留まるんですね。
ちなみに無限段階まで進めた時の見た目はこんな感じになるはず:

色が濃くなっている部分には辺がぎっしり詰まっています。実際には辺の太さは0なのでそこには無限に微小な面積が存在し、結果面積が2の正方形に見えます。なんだか不思議ですよねぇ~。
深掘:フラクタルのお話
今回の問題で出てきた図形。最初こそ正方形ですが、段階を踏むと辺に繰り返し構造が見られる特徴的な形になりました:

段を細かくしてもその辺に似たような形状が出現します:

このように図形の一部が元の図形と似通っているような図形を「フラクタル」と言います:
フラクタルは数学者のブノワ・マンデルブロさんが導入しました。マンデルブロと聞いて「マンデルブロ集合」を思い出した方もいらっしゃるのではないでしょうか?そうです、マンデルブロ集合を見つけたのはマンデルブロさんで、これもフラクタルの代表的な図形の一つです:

フラクタルは数学的に厳密な定義が難しいのですが、俯瞰的に見た図形と微視的に見た図形が似通っている(自己相似性)のが特徴です。
フラクタル次元
図形の一部が元の図形と似たような図形。そういうフラクタル図形の似通り具合の一つの指標がフラクタル次元です。
感覚的なお話ですが、たとえばとある図形があって、その図形を2~3に等分しただけで元の図形と相似なパーツが出て来る。その場合「自己相似性が高いなぁ」って感じませんか?一方で元のパーツを細かく裁断しても相似にならないパーツばかりだったら自己相似性が低そうですよね。この感覚的な自己相似性を数学者は数値化しようと考えました。
自己相似性がものすごく高い図形の代表は線分です。線分は2等分するだけで元の線分と相似な線分が出来てしまいます:

この「2等分したら元の図形の半分の大きさの相似な図形が出る」という似具合を、線分の次元数を取ってD=1と表現する事にしました。
では正方形はどうでしょうか?正方形は2等分だと長方形なので各パーツは正方形と相似になりません。4等分して初めて元の半分の大きさの相似な正方形になります。これは線分よりは分割数が多くその分自己相似性が低いと考えられます:

「4等分したら元の図形と半分の相似な図形が出る」この似通り具合を正方形の次元数である2次元を取ってD=2と表す事にしました。
そろそろお察しかもしれませんが、3次元の世界である立方体についても同じような考えが通じます。立方体は8等分してようやく各パーツが元の立方体の半分の大きさで相似になりますよね。「8等分で半分の大きさの相似」という似通り具合は3次元なのでD=3です。
一般に次元数が増える程元の図形を等分して相似な図形を作る事が難しくなります。D=4である4次元の世界にある立方体(超立方体)は16等分しないと元の図形の半分の大きさの相似な立方体にならないんですね。
ここまでの事からこの次元数Dと相似な図形になる分割数N、そして出来た図形の縮小サイズ1/Sとには、

という関係があるのが分かります。例えば3次元(D=3)の立方体なら半分のサイズ(S=2)でN=8個相似な立方体ができるので、上式が成り立っていますよね。もしサイズを1/3(S=3)にしても出来る個数はN=3×3×3=27ですからやっぱり上の式は成立しています。
上式は、

分割数Nと縮小サイズSから次元数を求める式に変形できます。このDを「フラクタル次元」と言います。感覚的にはフラクタル次元Dが小さい程全体と部分とが似てる(自己相似性が高い)と捉える事ができます。
凸凹正方形のフラクタル次元
さて、では今回の問題に出てきた図形のフラクタル次元はいくつになるのでしょうか?
フラクタル次元を考えるにはまずどの段階でも共通して出現する「基本図形」を抽出する事が第一歩です。今回の問題の図形を線で出来た図形と捉えると、繰り返し出現する図形は下図の凸形状の線分になります:

この基本図形から一段凸を進めた図形がこちら:

この図形の中に基本図形が何個入っているかと言うと…色分けしたように5つですね。そしてその一つのパーツは元の図形の1/3の大きさになっています。分割数N=5とパーツのサイズS=3があればフラクタル次元Dを求められます。すなわち、
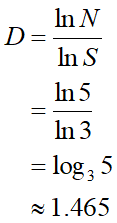
この図形のフラクタル次元は1.465次元という事になります!小数点の次元というのは感覚的にイメージできる物ではありませんが、この図形がフラクタル次元D=1の直線よりは自己相似性が低く、D=2の正方形よりは自己相似性が高いという事はわかります。
自然界にあるフラクタル
フラクタルは自然界にも色々と見られます。例えばロマネスコという野菜:
集合恐怖症の人は閲覧注意なのですがww、この野菜は星形のパーツの中にさらに星形のパーツが埋まっているようなフラクタル形状をしている事で知られています。
普通の人にしてみたら「へぇ~」ですが、これが生物学者にしてみると「いったいどういうシステムが働いてこのフラクタルが形成されるのか?」と興味津々になります。だって誰かがそういう配置になるよう手を加えたわけでもなく、ロマネスコが成長する過程でこの形状が自然と出来上がっていくんですから。しかもどのロマネスコも同じ性質を持っているので、これはもう環境では無くロマネスコのDNAの中に仕込まれていると言う事。いわばロマネスコの運命なんです。成長の過程で色々な作用が起こり結果としてこのフラクタルが生じてしまう。こういうのはホント生物の神秘性ですよね。
海岸線も自然界にあるフラクタルの一つとして良く知られています。海岸線を人工衛星から見るとギザギザしています。その海岸の一部を拡大してみてもやっぱり似たようなギザギザになっています。海岸線のフラクタル次元は場所により異なりますが1.2~1.3程度だそうです。今回の問題よりも値が小さいわけで自己相似性が高いですよね。
山脈もフラクタル図形です。大きな山も少し細部に拡大すると似たような凸凹が出てきます。そのフラクタル次元は2.2くらいとの事。
ゲームに出て来るフラクタル
実はゲームの世界でもフラクタルが利用されています。例えばオープンワールドの広大な地形を作りたいと思った時に、人の手でデコボコさせるのは非常に手間がかかります。そこで自動的に作ろうと考えるわけですが、その時にフラクタルを利用するんです。まず広い範囲で大きな周期を持ったカーブで凸凹させて、次にカーブのサイズを縮小して凹凸を足し合わせます。それを繰り返していくと見た事のあるような山々の景色になっていくんです。
先程山脈のフラクタル次元は2.2くらいだと言いましたが、この値は「次の段階でどの程度図形を縮めれば良いか」という目安になります。面積で言うと

およそ21.8%くらい、つまり縦横高さで言えば、

縦横高さを46.7%くらいに縮めた山を重ね合わせる、それが終わったらさらに46.7%に縮めたミニ山を重ね合わせる…というのある段階まで繰り返すと実際の山脈の形状に近くなると概算できます。面白い物でこのフラクタル次元から離れた倍率で重ねると、山の繰り返し感が強くなったり逆に山肌がつるっとし過ぎるなどやっぱり不自然さが際立ってくるんです。このようにゲーム制作ではフラクタル次元は案外役に立っているんです。
河川や樹木の枝、シダ、雲、人の血管など自己相似な図形は良く見ると身近に沢山あります。そしてそれぞれバラつきはあるもののある程度固有のフラクタル次元を持っています。皆さんも今回の問題のように図形を分割して元の基礎図形をくっつけてフラクタルな図形が出来ないか考えてみたり、身の回りを観察してフラクタルな図形を見つけてみると楽しいですよ。
ではまた(^-^)/
