閉じた水槽の中で増える生き物(解説)
問題はこちら:
答え:13世代目(Nn≒5592個体)
問題の条件でこの生き物は13世代目で個体数が5000を越えます。世代数自体は問題の漸化式をExcelやプログラムなどでくるくる回して計算すればすぐに求まります。各世代での個体数をグラフ化するとこんな感じです:

最初は個体数自体が少ないので増え方は微々たるものですが、7世代目あたりから伸びが顕著になって来て一気に増え始めます。でも数が増え過ぎると急ブレーキがかかり、限界の10000個体辺りで頭打ちになっています。このようなS字カーブを描くのがロジスティックモデルの特徴です。
実際に5000個体ジャストになるのは12世代と13世代の間位でしょうか。この厳密な所を求めるべく、深掘では高校数学の範囲で漸化式を解析的に求めてみます。
深掘1:漸化式を解いてn世代での個体数を求めよう
問題の漸化式を再掲します:

この漸化式はNnの2乗が入っているので「非線形漸化式」という部類になります。非線形の漸化式の多くは解析的に解けないのですが、実は上の式はスペシャルバージョンで解く事が可能です。ただ導出が少し難解で冗長なのでw、とりあえず先に解いた式を示しておきますね:

こんな形になります。では導出開始です。
元の漸化式を展開すると、

このように2次関数の形になっています(非線形型)。これを解ける形に持っていくため、

という定数Aが入った漸化式を用意します。このCnについて、

というべき乗の関係が成り立っていると仮定します。Bは定数です。このCnを元に戻して整理すると、

こうなります。この式と元の個体数の漸化式の定数部分を見比べます。まず、

ですね。また

もわかります。第3項の定数項はゼロにならないといけないのですが、実は求めたAとBを入れるとうまい事ゼロになってくれます。ここがスペシャルケースで、普通は第3項がゼロにならないためうまく解けないんです。
AとBが具体的に定まったので、後はCnの漸化式を解くだけです。手始めは両辺の対数を取って、
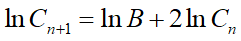
ここで、

と置くと上式は、

となります。lnBは単なる定数なので、これは高校で習う等比数列の漸化式の形になっています。

とするとα=lnBがわかり、

が導けます。後はDnと置いた所を戻していくだけです:

A=-L、B=-1/L、そして最初にN1=2匹水槽に入れたので、

無事n世代目の個体数を算出する式が導けました。
今回の問題はNnが限界個体数の半分となる世代数が欲しいので、Nn=L/2と置いて上の式をnについて解きます:

上式にL=10000を代入すると、

が求まります。12.758世代くらいで限界の半分になるので、13世代目にそれを越える事になります。
深掘2:個体数解析で使われるロジスティックモデル
今回の生き物の増え方を表した漸化式は「(離散)ロジスティックモデル」と呼ばれています。増える速度であるaを一般化した式は、

このような漸化式になります。a=1とすると今回の問題の漸化式と同じになります。aは理想環境での最大増加率で、Lはその生物がいる環境での限界個体数で「環境収容力」と呼ばれています。
aがとても大きいとその生き物は爆発的に増加していき、あっという間に環境収容力近くにまで達してしまいます。細菌などはその部類に入る生き物です。逆にaが0に近い値だとその生物は沢山の世代を重ねてゆっくり増えていきます。またもしaがマイナスになったら、その生物の集団は徐々に数を減らしてしまう事になります。国勢調査で日本の人口は徐々に減っている事が明らかになっていますが、仮にそれがロジスティックモデルに沿っているとするなら、このaが幾ばくかマイナスという事なんですね。
生物学の中でも個体数解析の分野ではこのロジスティックモデルは本当に良く使われています。この式をベースに、例えば被食者と捕食者がいる場合はどうなるか、同じ種でも年齢ごとに分けるとどうなるかなどより複雑なモデルが色々と考えらています。それらのモデルを対象とする種に当てはめてモデルの妥当性を検証したり、その種の未来の個体数を予想したりしています。
ただ上の離散的なモデルは一般には解析的に解けないため扱うに少し面倒な所があります。そこで多くの場合これを連続的なモデル(微分可能な式)に書き変えて利用しています。連続的なモデルの場合微分方程式を解く事が出来て、より具体的な研究が出来るんです。その辺りも非常に面白いのですが、今回は流石に冗長なのでまたの機会にご紹介できればと思います。
生物の研究って自然の中で生き物を観察したり集めたりしてるのかな?という漠然としたイメージがあるかもしれませんが、観察は勿論の事数学もバリバリに使います。観察した事を科学として昇華させるには、客観性の高い数学(モデル)で語る必要があるんですね。
今回の問題のように、皆さんが学校で勉強している勉強が大学の研究や社会でどう活用されているか、今後も沢山ご紹介出来ればと思います。それを通して「なぜ勉強が必要なのか」という事の意義を感じて頂けると嬉しいです。
ではまた(^-^)/
