円周率の日記念、小さい円の面積は？（解説）

問題はこちら：

答え：π

　小さい円の面積はπになります。円周率の日記念ですから、この答えが欲しかったww。どのように求めるか解説します。

解説：接する円の性質と三平方の定理で

　求めたい緑の円の半径をxとします。このxを求める為に補助線を幾つか引いてあります。本当はこういう補助線が引ける根拠をちゃんと示さないといけないのですが、それは深堀に回すとしまして(^-^;、まずはある程度自明として答えまでの道筋を進む事にします。

　点Aは大きい円の中心、点Bは中くらいの円の中心です。図から中くらいの円の半径は大きい円の半分なのでABは3/2になります。

　点Eは中くらいの円と小さい円の接点です。BEも中くらいの円の半径なので3/2、よってBCは

となります。

　次にA、C、Dの関係に注目です。点Cは小さい円の中心です。Dは大きい円と小さい円の内接点です。ここからADは大きい円の半径なので3とわかります。ここで図の対称性からAとCとDは直線状に並んでいる事がわかります。ここからACは、

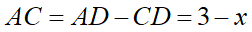
と表せます。

　ここで⊿ABCに注目します。ABに対して図の対称性から∠BACは垂直です。よって⊿ABCは直角三角形なので、三平方の定理で各辺の関係を表現できます：

xについての方程式を解くと、

小さい円の半径xが1だとわかりました。ここから小さい円の面積Sは、

という事で円周率の日にちなんだ面積πが求まりました(^-^)

深掘1：中くらいの円の半径は大きい円の半分なの？

　ここからは深堀です。解説では色々な事を自明として道筋を進めましたが、ある程度根拠を示さないといけない個所がいくつかあります。その一つが上の命題です。

2つの外接する円には共通接線がある

　問題にある2つの中くらいの円は合同で互いに外接しています。また大きな円に内接しています。問題では中くらいの円の半径は明示しておらず「こういう接し方で一番大きい円」としています。という事はこの条件の下で中くらいの円の半径をちゃんと求めないと本来はいけないわけです。

　　互いに外接する2つの円には共通接線がある事をまずは示しましょう。
　滑らかな曲線上の一点に接する直線を「接線」と言います。曲線の一つである円の接線には「中心と接点を通る直線と接線は垂直に交わる」という性質があります。これは中学で習う定理ですが、その理由を復習してみましょう。

　上図のように円周上に点ABを適当に取って、中心Oを含む⊿OABを作ります。ABの中点をCとし、⊿OABを⊿OACと⊿OBCに分けます。OA＝OBでOCは共通、そしてAC＝BCですから⊿OACと⊿OBCは合同です。∠ACBは180°で合同より∠ACO＝∠BCOなので∠ACOは90°となります。

　ABは円周上の適当な2点だったので、それをどのように取っても同じ事が成り立ちます。そこで点Cが同じ直線上に位置するようにしながらABをどんどん近付けていきます：

すると∠AOCは常に直角を維持するため、どの直線ABも並行になるのが分かります。そしてABが円周上に到達した点Cの所に集約する瞬間も同様の直線が引けることになります。この直線は円と1点Cで交わっているので接線で、また図中のどの直線ABとも並行です。ここから中心と接点を結ぶ直線と接線は垂直に交わる事がわかりました。

　厳密に言うとこの証明はちょっと不正確なのですが（ABCが接点で一つになった時に三角形の合同条件が破綻する為）、間違っているわけでもないためここではさらなる深掘りは割愛します。

　上の円の接線の性質から、2つの円が接する時、

その接点で2つの円は共通接線を持ち、上図のように接点から互いの中心点を通る垂線を引く事ができます。この接線に垂直な線を「法線（normal line）」と言います。

中くらいの円を最大にしたらその半径は大きな円の半分になる

　さて、大きな円にこのだるま型の図形が内接しているわけですが、半径について条件が無いとこんな内接の仕方もできてしまいます：

　ここから単に2つの円が大きな円に内接するというだけでは中くらいの円の径が定まらないんですね。そのため問題では「半径が一番大きくなる」という条件が付記されています。

　上図から言える図形の性質を整理しましょう。大きな円の円周上にある2つの接点から引いた法線はそれぞれ大きな円の直径になるので、その交点は大きな円の中心になります。接点が共通しているので、その法線上に中くらいの円の中心がそれぞれ位置するのも明らかですよね。これらは中くらいの円の径が変わっても共通する性質です。

　ここからさらに大きい円の中心と中くらいの円の接点を通る直線Lを引く事を考えます：

図の青い線と緑の線で囲まれた三角形に注目すると、青い2つの辺は同じ長さで、緑のrも上下で同じ長さなので、三角形は二等辺三角形になります。直線Lが二等辺三角形の頂角から対辺の中心を通っているので、直線Lと中くらいの円の中心を通る直線とは垂直に交わります。直線Lは中くらいの円の接点を含んでいるため、直線Lは2つの中くらいの円の共通接線である事がわかります。

　中くらいの円の半径rが変化してもこの関係は変わりません。ここから、

接点を接線L上でスライドして、上図のようにそれにフィットする2つの中くらいの円を描く事ができるのがわかります。そして接点を大きい円の中心と重ねた時、2つの円の法線と円の直径とが重なるのもわかります。円の中で引く事ができる最長の線分は直径なので、この位置で真ん中の円の半径も最大になり、それが大きい円の半分になる事も同時にわかります。

深掘2：A,C,Dが一直線になる？

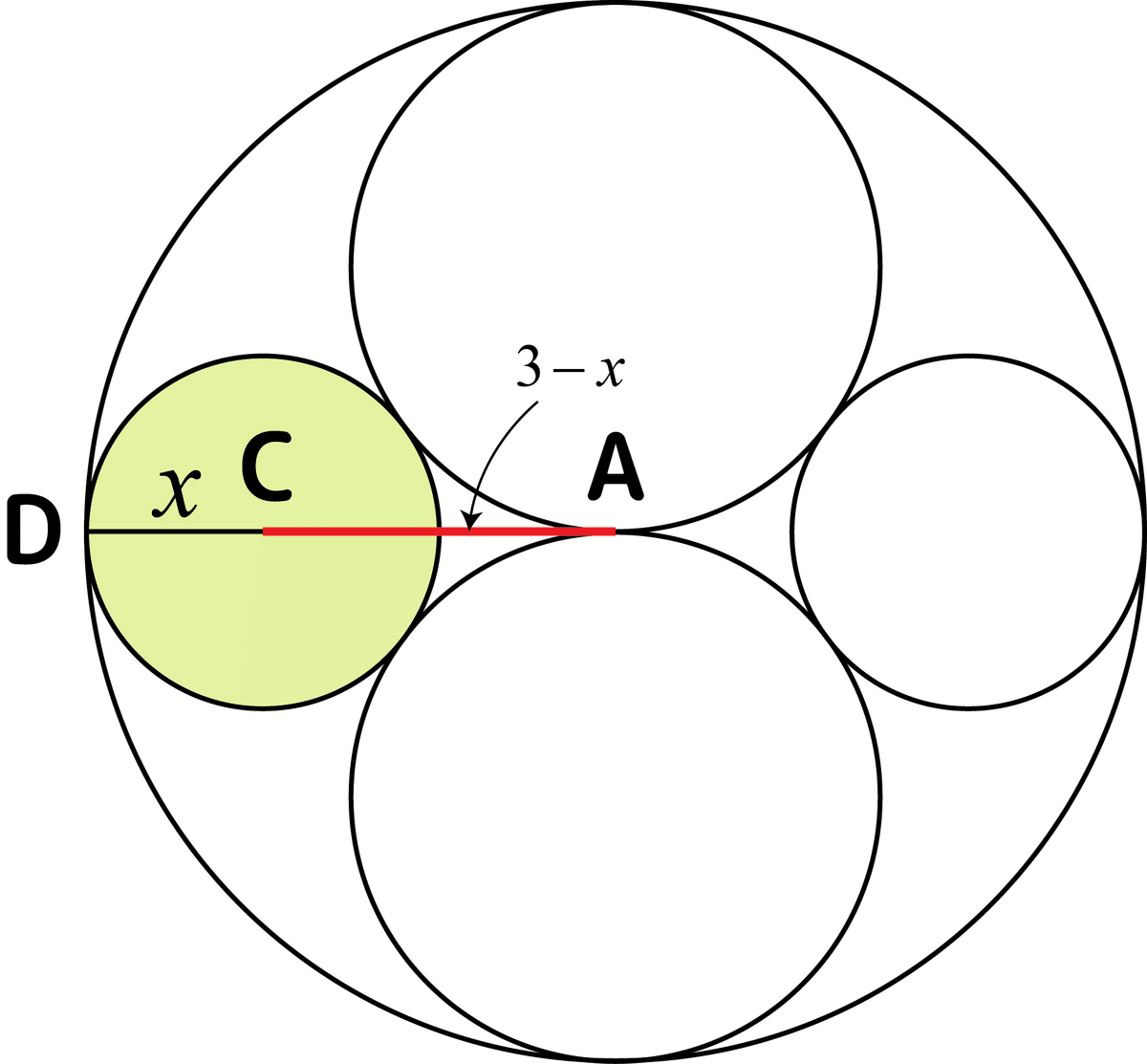
　導出の最後の方で、上図のA、C、Dが直線上にあるのでACの長さが3-xになるという事を自明として進めました。これも「本当？」って言われるともごもごしてしまうかもしれませんね(^-^;

　点Dは大きい円と小さい円の接点です。深堀1でも示したように、接点を通る接線とその法線は垂直に交わります。つまり、

直線Lが2つの円の共通接線になっているので、線分ADとCDはそれぞれ点Dを通る法線に重なっています。これでA、C、Dも同じ直線上にある事が証明できました。

深掘3：∠BACが垂直？

　三平方の定理を使うためには⊿ABCが直角三角形である必要があります。解説では図の対称性からそれを自明としました。これもちゃんと証明しておきましょう。

　上図でB、A、F（上の円の中心）が一直線上にあるのは深堀1で示した通りです。よってAB=AFが言えます。次にBCとCFはそれぞれ中くらいの円の半径と小さい円の半径の合計になっているのでBC=CFも言えますね。ここから⊿CFBは二等辺三角形になります。CAは二等辺三角形の頂角からその対辺の中心点に下した線分になっているので∠BACが垂直になる事がわかります（⊿AFCと⊿ABCが合同という所から∠BACが垂直と言ってもOK）。ここから⊿ABCは直角三角形である事が証明できました。

　ちなみにですが、この三角形ABC、皆大好き3:4:5の直角三角形になっている事にお気付きでしょうか？

この比の三角形が円で構成された図形から出てくるのは予想外でした。問題を作った後に気付いて「へ～」と驚いた点ですww

　という事で今回は円周率の日にちなんだ問題でした。ではまた(^-^)/