数字の桁を2乗して足す…を繰り返すとどうなる?【問題】
問題はこちら:
答え:どんな正数でも特定のループを繰り返す
「各桁を2乗して足す」を繰り返すと、どんな正数でもいずれは特定の数列が繰り返し出現するようになります。それこそ100桁、1000桁の巨大な整数でも!ですから問題にある「(C) 特定のループを繰り返す」が正解です。何となくそうだよな~という感じはするかもしれませんが、なぜそうなるか?をここでは詳しく解説します。
解説1:必ず起こる「桁下がり」
今回の「各桁数を2乗して足す」という計算を以後「変換」と呼ぶことにします。
正数の各桁は0~9のいずれかですから、変換後の値が最も大きくなるのは各桁が全部9の時です。これは自明ですよね。例えば999は変換すると9×9+9×9+9×9=81×3=243となり、これが3桁の正数の変換で最大となります。このすべての桁が9である999…999の変換を一般化してみる所から始めましょう。
n桁の999…999の変換をx(n)と表現します。これは9がn個あるわけですから、

となります。x(n)の桁数mは常用対数を用いて、

と計算できます。ここで[ ]はガウス記号で、中の数字を越えない最大の整数を表します。[3.14]なら3です。常用対数の計算結果だけだと桁数が1つ少なくなるので、上では1足して桁数にしています。例えば1000は4桁ですが、log10(1000)=3と1桁少ないですよね。
この式から1桁の9は、
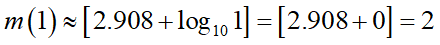
で2桁(81)、4桁の9999なら、

で3桁(364)とちゃんと桁数が計算できてますよね。もちろん任意の9999…999の変換後の桁数もこれで計算できます。
さて、今回の変換で「元の数字より変換後の数字の方が桁数が少なくなる」というのは大きな意味を持ちます。上の例でも4桁の9999は変換すると364で3桁に下がっています。9999は4桁の数字の中で変換後の値が最も大きくなる数字ですから、それが3桁に下がるというのは「どんな4桁の数字も次の計算で3桁以下になる」という証拠になります。これを「桁下げ」と呼ぶ事にしましょう。
では5桁では?100桁では?それ以上の桁数でも桁下げは常に起こるのでしょうか?結論から言うと、4桁以上のどんな桁数の正数でも計算を繰り返すと桁下げが起こり3桁以下になります。これを示してみます。
元の999…999の桁数nに対してm(n)が1以上少なくなれば、n桁のすべての正数で桁下がりします。つまり、

を言えば良いわけです。ただm(n)にはガウス記号が入っていて不連続でちょっと扱いが面倒…。なのでガウス記号で包む前の小数点付きの式を使う事にします。それをa(n)とします:

この場合桁下がりの条件は、

です。上の不等式の左辺をy(n)として展開すると、

このy(n)がゼロ以上になるnについて検証します。その為にはこの関数の形を知りたい。そこでnで微分して増減を見てみましょう:

nは1以上でln10>1なので、この微分式はn≧1の範囲で0より大きいのが分かります。つまりy(n)は単調増加関数です。よってy(n)がマイナスからプラスになる境界となるnを調べれば、そこから先の桁数で桁下がりする事を言えます。
実際にy(n)にn=1から順に桁数を入れていくと、

となり、n≧4以上は0以上になっています。つまりn≧4桁の正数は変換を繰り返す事で高々3桁の数字に落ち着く事がわかりました!
ここまでのお話で問題にあった「(A)値が増え続ける」が無い事も確定ですね。
解説2:変換したら常に3桁以内になるのでループすると言える!
解説1でどんな正数も変換を繰り返すと1~999までの最大3桁の数字のいずれかになる事がわかりました。実はこの段階でもう「特定の数列がループして出現する」が言えてしまいます!決め手は「鳩の巣原理」です。
鳩の巣原理とは多数の物があって、その物のパターン数が限られている場合、物がそのパターンより多ければ必ずパターンが重複した物がある、という形式になっている問題を言います。言葉で言うと何だかよく分からないかもしれませんが、具体例を見れは何て事はありません:
「鳩の巣が10箱あります。鳩が11羽いてみんな巣箱に入ったとすると、2羽以上の鳩が入っている巣箱はあるでしょうか?」
各巣箱に1羽ずつ鳩を入れるには10羽いればよく、11羽目の鳩が1羽余ります。この余った鳩をどの巣箱に入れてもその巣箱は2羽になってしまいますよね。ですからこの問題の答えは「2羽以上の鳩が入っている巣箱はある」となります。

「こんなの当たり前じゃん」と思った方。その通りなんです。鳩の巣原理って至極当たり前の事を言っているに過ぎません。この当たり前が、実は今回の問題にもまんま当てはまっています!
どんな正数も変換を繰り返すと1~999の3桁の数字のいずれかになります。高々3桁になった後は4桁以上の数字に桁上がりする事はありません。解説1でそれを証明しました。つまりその後に出て来る数字のパターンは最大でも1~999の999パターンしかないんです。一方でこの変換は永遠に続ける事ができます。高々3桁になってから変換を999回繰り返すと、高々3桁の数字が1000個並ぶわけです。ほら、999パターンしかないのに(999個の巣箱しかないのに)高々3桁の数字が1000個並ぶ(1000羽の鳩がいる)って事は、この数列の中に同じ数字が少なくとも1個はあるって事なんです。鳩の巣原理の図式になっていますよね!

変換を繰り返して過去に出た数字が再出すると、そこから先の数列が以後繰り返し出現する事になります。これは今回の変換が1対1対応になっているからです。もし変換後の数字が不確定だとこれは言えませんが、確定なので繰り返し出現すると断言できるわけです。
という事で、正数の桁を2乗して足すを繰り返すと「(C) 特定のループを繰り返す」というのが答えだとわかりました!
深堀1:ループパターンはいくつある?
ここからは深堀です。すべての正数を今回の計算にかけ続けるとループする事がわかりました。では、具体的にどういったループになるのでしょうか?
これはですね、流石に1~999までを虱潰しにチェックしないとわかりません(^-^;(もう少し深堀りするなら1~162まで検証すれば事足ります)。という事でプログラムを作って回してみました:

出力結果だけで申し訳ありませんが、結果として2つのパターンしかない事がわかりました。一つは「1」が永遠に続くループ。これは例えば10とか100などが数列に出てくると途端に1に落ち着きます。もう一つが「{4, 16, 37, 58, 89, 145, 42, 20, 4}」というひと塊のループ。こちらの方が圧倒的に多かったです。そして面白い事にこれ以外のループは存在しません!
ありとあらゆるすべての正数について、各桁を2乗して足すを繰り返すと、1の自己回帰ループかもう一つのループのどれかに辿り着く。興味深いですねぇ~
深堀2:3乗以上ではどうなのか?
それでは各桁を2乗じゃなくて3乗とか4乗などもっと大きな乗数にしてもループするのか?
ポイントは2乗の時と同じで「n桁の9999…99を変換した結果桁下がりが起こるか?」です。これが確認できればループに落ち着きます。
変換時の次数をaとします。n桁の9999…999を変換した時の値は、

です。この桁数は、

と表現できます。元の桁数nに対して次の数字の桁数ma(n)は高々対数レベルの桁数になるので、nがある程度大きくなった段階ですぐに桁下がりが発生するのは明らかですよね。また次数aは定数項にしか無くnに干渉していないので、aが大きくなってもこの桁下がりの傾向は変わりません。
つまり、乗数がどれだけ大きくてもある桁以上は必ず桁下がりを起こし、その桁以下のパターンしか出てこなくなるので、鳩の巣原理からやっぱりループするんです!
試しに3乗でプログラムを回して見た所、ループパターンが増えました。「1」は相変わらずありますが他に「153」「370」「371」「407」も自己回帰する事が判明。確かに371の各桁を3乗して足しても371です!複数個のループは「{55,250,133}」「{919,1459}」「{160,217,352}」「{136,244}」の4パターン。これが3乗の全ループパターンです。
4乗の自己回帰パターンは1, 1634, 8208, 9474の4つ。(8^4)+(2^4)+(0^4)+(8^4)=4096+16+4096=8028!確かになります!そして複数個のは「{2178, 6514}」と「{1138, 4179, 9219, 13139, 6725, 4338, 4514}」この2つ。4乗だと次の値に1万台も出るくらいなのに、それでもやっぱりあらゆる正数がいずれちゃんとこれら数種類のループに辿り着くのだから不思議。ただただ面白いです(^-^)
深堀3:コラッツ予想
今回のように元の数字に何らかのルールで変換をかけ次の数字を求めるという問題の中で「コラッツ予想」というとても簡単で不思議な変換があります。
「元の数字が偶数なら半分に、奇数なら3倍して1を足す」
ルールはこれだけです。実は、この変換を続けると最終的に1になってしまうという予想が立てられています。例えば19だと、
19→58→29→88→44→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
と増えたり減ったりを繰り返して1が出てきます。他の数字でも1になるのを確認できますので皆さんもやってみて下さい。
2024.12現在、コラッツ予想は証明されていません。なぜ最終的に1になるのか完全にはわかっていないんです。こんな簡単な変換なのにです!もし変換して一つでも過去に出た数字が出てくれば、それでループが確定するので、コラッツ予想は間違いと言えますが、現在2の68乗までの正数について反例が無い事がコンピュータの計算によって確かめられているそうです:
皆さんも今回の問題もそうですし、コラッツ予想のようなルールを自分で決めてみて、計算を繰り返してどうなるか色々遊んでみると面白いですよ。もしかしてそこからコラッツ予想を証明する(もしくは予想を覆す)発見があるかもしれません!
ではまた(^-^)/
