1^x=-1を満たすxは?(解説)
問題はこちら:
答え:以下の通り

ただし、n,mは

となる整数とします。
今回の問題、xは上の分数を満たす「有理数」になります。式として書くと、

です。
「いやいやいやいや、それはおかしいでしょ!xが複素数なら何か答えが-1とかなりそうな気もするけど、1の有理数乗は流石に絶対1だよ!」これ、僕は最初マジでそう思いました。だってもし上の式が正しいのなら、例えばn=1、m=0の時に

ってなるのですから。ルートは中が正の実数なら0以上の実数のはず。そもそもルート1は1のはず!そうじゃないなら、高校まで習った数学が根底からガラガラと崩れ落ちてしまいます。いったいこれは何が何やら…。
これがどういう事か、解説します。
解説1:1は実は沢山ある!
今回の問題、真相はこれにつきます。1は、実は複素数の世界まで広げると沢山あるんです。
複素数で1というのは、複素平面だとここです:

Rは実数軸、Iは虚数軸です。数字として1を表記するなら、

ですから上の赤丸の位置になります。複素平面で見る限り、1はこれ一つに見えます。
ここからが面白い所。1を極形式で表現し直すと、こうなりますよね:

nは整数です。オイラーの公式、

でθに2nπを入れると、上の式になります。確かにこれはどの整数nでも1+0iです。でもnは任意の整数なので、形としては、

と沢山の複素数の表し方が出来ます(もちろんnはマイナスもあります)。

ところで複素数の定理の一つに「ドゥ・モアブルの定理」というのがあります。これは高校で習いますね。どういう定理かと言うと「複素数の累乗とは複素平面上での回転角度の倍数の事である」という物です。例えばθ=30°で大きさ1の複素数、

を2乗すると、

このようにθ=60°と回転角度が2倍で大きさ1の複素数になりました。累乗すると複素数は累乗倍回転するんです:

2乗ではなくて1/2乗すると、ドゥ・モアブルの定理から回転角度は半分になります。では、先程の「1」達をすべて1/2乗してみます。つまり回転角度に1/2を掛け算すると…

ここで「ああ!!」っと思った方はvery good。そうなんです、同じ1でもθ=0の場合は1/2乗しても0ですが、θ=2πの1は1/2乗する事で半分のπになります。大きさ1でθ=πの複素数は…そう-1です:

先程まで同じ1だったものは「同じように見えていた」だけで、実は性質が違う異なる「1」なんです!
解説2:問題の「1」を複素数にして解く
ここまでを踏まえ、問題の式にある1を複素数で表現して書き直してみましょう:

n,mは共に整数です。ただしn≠0とします。左辺の「1」は数直線の右側を起点として2π毎に同じ点に重なるので左辺のような表現が出来ます。一方で「-1」は数直線の左側を起点として同様に2π毎に同じ点に戻って来るので右辺の形で表せます。
ここで両辺の対数を取ると、

このようにxが有理数として求まります。そしてこの式が成り立つ必要条件は、左辺の1が、

で、右辺の-1が、

の時です。n=0の時の1は回転出来ないため累乗して-1になる解は存在しません。
深掘:多価関数と主値
私達が認識していた「1」を複素数の世界まで広げると、同じ1でも性質の異なる1が存在しているのが分かりました。これを一種の関数とみなすと、

こんな表現になるでしょうか。右辺に入れた実数の複素数バージョンを返してくれる関数です。これ、高校までに出て来る関数とは一味違います。高校数学で習う関数というのは、
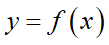
こんな感じで何か値xを関数に入れると答えyが一つだけ出てきます。つまり1対1対応がある関数です。しかし先の関数は値1を入れると1を表す無数の答えが出てきます。これは1対多の関数です。こういう関数を「多価関数」と言います。複素数の多価関数の場合、今回のように2nπ毎の周期性を持った複素数が出力されます。
実数を複素数に変換する多価関数が出力する無数の複素数は、今回の問題のように非常に興味深い、そして私達の感覚と時に異なる振る舞いをします。ただその場合一般的な感覚で検討する事が難しくなってしまいます。例えば、

こうだよと言われても困ってしまいますよね。その左辺の1はどの1だい?って事になる訳です。
そこで複素数の回転角度を-π≦θ≦πの範囲に限定し、それで議論する事で一般感覚を保つ事にしました。この範囲にある複素数を「主値」と言います。主値であれば、

と、高校で習った累乗の性質がちゃんと再現されますし(左辺の1はθ=0なのでドゥ・モアブルの定理で回転が1/2倍になってもθ=0)、主値の範囲にある実数は高校の時の実数と同じ振る舞いをしてくれます。そして主値のみを扱う事で多価関数は私達になじみ深い1対1対応が取れた一価関数になります。
終わりに
今回の問題、僕は「複素数の世界というのは何と深淵な…」と畏怖の念を抱いてしまいました。深淵を覗くと深淵もまた覗き返して来るなどと良く言いますが、そういう感覚を覚えました。これ以上の深い所は大学で習う「複素関数論」で学べます。興味のある方は飛び込んでみても良いかもしれませんね。
ではまた(^-^)
