山をぐるぐる回る登山道の長さ(解説)
問題はこちら:
答え:登山道は対数螺旋(ベルヌーイ螺旋)になり、長さは約13637m
牛蹄山の山肌に沿った今回の登山道は、真上から見ると対数螺旋(ベルヌーイ螺旋)になり、その長さはおよそ13637mになります。

中学生と高校生の皆さんは真面目に解く事はちょっと難しいのですが、上手に考えると登山道の長さは求められます。まずはその方法を解説します。その次に大学生以上の皆さんに考えて欲しい対数螺旋になる理由、そして曲線の長さを真面目に解く方法を解説します。
解説1:斜度8度で固定という事実を利用する
まずは中学生、いや小学生でも求められる方法です。
今回の登山道、道が上のような左回りの渦を巻きそうだな~というのは何となくイメージできますよね。でもこのままだとどう長さを求めて良いか路頭に迷います。そこで「山肌に沿っている道のどの場所で測定しても坂の角度は8度固定である」という条件を利用します。道が曲がっているからわかりにくいわけで、条件を外さないようにして真っすぐにしちゃいましょう:

すると上図のような直角三角形になります。赤い斜線Dが登山道で、確かにどこの地点でも斜度が8度ですよね。そして道は頂上まで続いているのですから、高さは1898mです。この直角三角形の辺の比は1:0.13917です(これは問題で示しています)。ここから、

登山道が約13637mである事がわかります。
解説2:曲線の「方向」を表すには?
解説1の方法は直感的ですが「本当にそれで良いのか?」という点で厳密性にちょっと欠けてはいます。また真上から見た時にどういう曲線を描くかという問いには答えられません。その辺りはやはり真面目に解くしかないかなと思います。ここからは大学生以上の方への解答です。
解答するに当たり少し前知識が必要なので、最初にそれを説明します。
今回の登山道はどの位置に立っても斜度が8度です。斜度…別の言い方をすれば傾きです。傾きと言うと私達は中学で直線の傾きを習い、高校で「傾きとは微分である」と習いました。例えば、

このxに対する傾きの大きさは、上式をxで微分した式、

で表現されます。ここからx=2なら傾きの大きさは4などとすぐに計算できます。この傾きの大きさというのは「xが1増加した時にyがいくつ大きくなるか?」という事だと習ったと思いますが、これはよくよく考えると方向、つまりベクトルになっています:

傾きをベクトルとイメージすると、単に接線云々だけでなくその点がどういう方向へ向かおうとしているかという情報も含んでいる事を明確に意識できます。
さて、世の中y=~と表す事が難しい関数もいっぱいあります。例えば半径rの円の方程式は、

ですよね。この円周上の一点Pはやはり傾きを持っています。もちろん上式をy=~の形に変形してそれを解く事もできますが、中心角θを媒介変数として上式を、

と極座標に書き変えた方が便利です。両方をθで微分し、それらを成分としたベクトルをvとすると、

これが中心角θに対応する円周上の点の方向ベクトルになっているのがわかります:

θがちょこっと増えた時(dθ)、xはdxだけ増えて、yはdyだけ増える。そんなイメージです。
これはもちろん3次元座標でも同じです。点P(x,y,z)の位置が何らかの媒介変数θのみで表現できるなら、その点Pが描く軌跡の方向ベクトルvは、
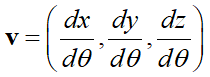
と表現できるわけです。
「媒介変数で表現される関数の方向ベクトルは各成分で微分した要素を並べれば良い」。この事実をベースに以下に進みましょう。
解説3:登山道を媒介変数θで表現してみよう
解説2の前知識を踏まえて、円錐形である牛蹄山の登山道を極座標形式で表現してみます。
牛蹄山の底面の中心を原点に定め、その半径をr0とし、山の高さをhとします:

山を真上から見る事を以下俯瞰図と呼ぶ事にします:

俯瞰図上で登山道の入り口がX軸上(r0,0)にあるとし、そこから左回りに道が伸びるとします。登山道上の1点Pまでの回転角をθと定めます。このθを媒介変数として点Pを極座標で表現する事を考えます。
点Pまでの俯瞰図半径をr(θ)とします。今回の登山道は斜度が一定なので上るほど、つまりθが大きくなる程頂上に近付くはずです。そこからr(θ)はθが大きくなる程小さくなっていく事がイメージできますよね。
点P(x,y,z)に1対1応した俯瞰図半径r(θ)があるので、そこからPxとPyは、

と極座標で表現できます。残る点Pの高さであるPzは、山が円錐形である事から半径r(θ)とr0、そして山の高さhの比から求める事ができます:

上の模式図から以下の比が成り立ちます:

これでPzもθのみで表現できました。改めて点Pの媒介変数表現をまとめると、

θのみで登山道上の点Pの座標を表現できています。ただしr(θ)の式の形が定まればの話です。つまり上の段階ではまだこの式は「円錐表面をくるくる回りながら描かれる何らかの曲線」を表しているにすぎません。例えばr(θ)=r0と固定しているとしたら、P(Px,Py,Pz)は底面の周囲をぐるぐる回るだけになりますよね。
よって今回の問題の条件に合致したr(θ)を定めるのが次の目標です。
解説4:登山道の方向ベクトルvからr(θ)の形を求める
解説2で述べたように、ある中心角θでの登山道の方向ベクトルvは、媒介変数で表されたP(Px,Py,Pz)をそれぞれθで微分すると表現できるのでした。とは言ってもr(θ)は今まだ定まっていませんので、r(θ)をθで微分した式をr'(θ)としておきます。上式をそれぞれθで微分すると、

こうなります。登山道のθに対応する方向ベクトルvは、

となるわけです。
さて、牛蹄山の登山道の条件は一つだけ「斜度8度」です。これは登山道の方向ベクトルvと水平面とがなす角度がどの点P(すなわちどのθ)においても8度で一定であるという事です。ここでは斜度をαと一般化して以後展開していく事にします。
下図をご覧下さい:

ベクトルvがどういう方向を向いているかはr(θ)が定まっていないのでまだぽやんとしていますが、少なくともvと水平面が成す角度は上図の斜度αなのは確かです。ここからこのαとベクトルvの大きさ|v|、そしてベクトルの高さvzに、

この関係があるのがわかります。三角関数の定義そのものですね。
vzは微分の形でわかっているので、残る|V|を展開します。ベクトルの大きさは各成分のべき乗の和をルートすれば求まります。記述がごちゃーとするので、

と簡略表記で置き換えて頑張って展開します:

途中展開はさて置き、結果的にルートの中にあったsinθやcosθが相殺して綺麗に無くなってしまいます。これを先の三角関数の関係式に代入してさらにうりゃりゃっと整理すると、

最終的に最下段まで簡単になります。この最下段の括弧の中はすべて定数です。そこで、
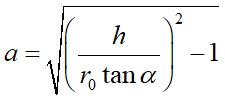
と置き換えるとこの式は、
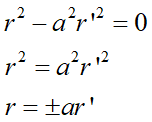
こんなとてもシンプルなr(θ)の微分方程式になってしまいます。ただしa>0が条件です。
上の微分方程式は高校でも習う変数分離型なので簡単に解けます:

θ=0の時にr(θ)=r0だったので、積分定数Cは、

よってr(θ)は、

となります。ここまで±がある2本の式を一緒に求めましたが、r(θ)は山に登るならr0以下なのでマイナス側である、
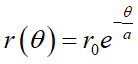
を採用します。このr(θ)が今回の問題の条件に合う半径の関数です!
このr(θ)をPの各成分の式に改めて代入すると、

このようになり、中心角θのみで登山道上の点Pが一意に求まるようになりました。ただしaは、

の定数です。
俯瞰図で見た場合Pzは無視されて(Px,Py)の2次元の図になります。式はθの値によって半径r(θ)が指数関数的に変化しています。これは対数螺旋(ベルヌーイ螺旋)に他なりません:
同じ斜度を保った登山道を作ると俯瞰図が対数螺旋になるというこの性質、非常に趣深いですよね(^-^)
解説5:螺旋の長さを求めよう
今回の問題はここで終わりません。さらに登山道の長さを求めなければなりません。大変…(^-^;
点Pはすでに媒介変数θで表されています。その場合0≦θ≦βの範囲で点Pが描く軌跡の長さDは、

上式で求める事ができます。これはいわゆる曲線の長さの式ですね。
式中のルートは方向ベクトルvの大きさ|v|そのもので、それは、

だったのでした。上式のr=r(θ)はすでにわかっているので、その微分式のr'(θ)を求めると、

右辺のように元のr(θ)で表現し直せます。これを|v|に代入すると、

このように中心角θを含むr(θ)がうまい事ルートの外に出る式になります。そしてルートの中はすべて定数になります。つまり方向ベクトルvの長さは半径に比例するんですね。
このルートの中もaを戻すとさらに色々消えてくれます:

分母にaを残している理由は距離の計算の過程でそれが消えてくれるからです。
ルートの中は今や斜度αのみになりました。これ、実はすっごい簡単になります:

ここから、
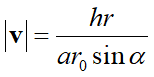
となりました。では距離Dの式を展開しましょう:
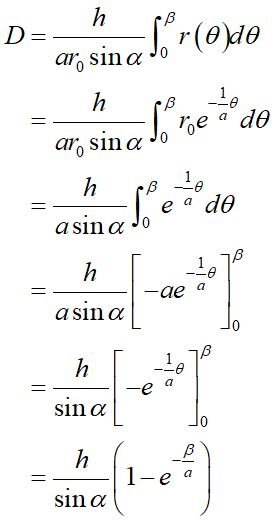
このように解く事ができます!ありがたい事に対数螺旋の長さは解析的に解けるんです。
上式のβは回転θの上限です。登山道が山頂に達する時のθは、Pz=hになるθを求めれば良いので、

ここから最終的に山頂までの距離Dは、

この超超シンプルな式で計算できるようになりました!展開の途中で様々な物が相殺して消えて行き、こんな単純な式にまでなってしまう。ぼくはかなり驚きました。この式は解説1で示した直角三角形の斜辺の長さを求める式そのものにもなっていますよね。
そして、式の中に半径の情報が入っていないのも驚きです。つまり特定の斜度を持った登山道の距離は山の底面の半径には関係なく山の高さにのみ比例するという事なんです。底面の半径が5kmの牛蹄山でも半径が1kmの尖がり山でも、斜度と高さが同じなら登山道の長さはなんと一緒です:

上図の左右は高さが同じ円錐で、登山道の斜度も一緒。この両者の登山道は同じ長さとなる…にわかに信じられませんが実際そうなります(^-^;
では最後の仕上げ。距離Dの式に牛蹄山の具体的なパラメータを入れて距離を算出しましょう。高さh=1898m、そして斜度α=8°を突っ込みます:

という事で登山道の長さは山頂までおよそ13637mである事が計算できました!
深掘1:実際の山の登山道の長さと比べてみよう
解説5で算出した登山道の長さを求める式D。この式から算出される長さと実際の山の登山道の長さを比べてみましょう。
登山情報を掲載している「やまクエ」さんのページに公開されている北海道の中級者向けの山から平均斜度と標高差の情報をピックアップし、実際の登山道の長さと先の式Dで求めた距離とを比較してみます:

[距離]の列がサイトに掲載されている距離で、[D]の列が計算で求めた距離です。見比べるとかなり近い距離が求まっているのがわかります!もしかするとサイトのも似たような式で近似した距離かもしれませんが、大外しはしていない事から、今回の問題で導出した登山道の長さを求める式は中々いい線いっているみたいです。
深掘2:aが成立しない場合
導出の中でtanが含まれる以下の定数をaと置きました:

aは実数なのでルートの中は正でないといけません。これが成立しない条件を探ってみましょう。
上式のルートの中が負になるとアウトですから、
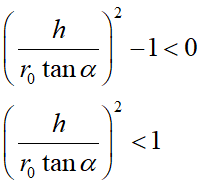
これが満たされてしまうとダメと言う事です。高さhも半径r0も正で、斜度αは90°以下ですからtanαも正。つまり左辺のパラメータはすべて正なので、

上式の左辺は何か?これは山の稜線の斜度Sのtanです。tanは0°~90°の範囲では単調増加なので、上式が成り立つというのは斜度αが稜線の斜度S以上になっているという状態。そんな登山道を作るのはもちろん不可能ですよね。
終わりに
今回の問題は答えを導くまで中々骨が折れる式展開を要しましたが、その結果円錐形の表面に描くパスに非常に興味深い性質があるのがわかりました。山の高さと登山道の斜度があれば、登山道の距離は物凄く簡単に式で計算できます。そして斜度と高さが同じなら、円錐の底面の半径に関係なく登山道の長さは同じになる。この性質については僕も式を導出して初めて見い出せたので「え~~~!すっご!」っと声を出して驚きました。ホント幾何学の神秘ですよねぇ。図形の表面にパスを描くシリーズ、他にも面白い物を思い付きましたらまた問題にしてみようと思います。
ではまた(^-^)/
