偽物の薬瓶はどれ？（解説）

　問題はこちら：

答え：例えば以下のように取り出す

1番から1単位（錠剤1個）
2番から1単位（錠剤2個）
3番から3単位（錠剤9個）
4番から1単位（錠剤4個）
5番から4単位（錠剤20個）

　各瓶から錠剤が連結しているブリスターパックを上の単位数で取り出し重さを測定すると、各瓶の真偽のパターンにより以下の32通りの重さが計測されます：

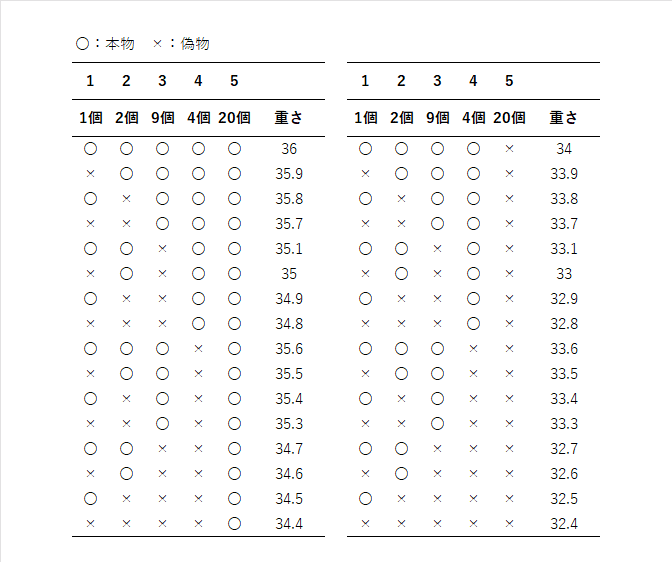
　〇が本物、×が偽物の錠剤です。全て本物の36.0gから全て偽物の32.4gまでの範囲でどのパターンにも重さの重複がありません。よって計測された重さから逆に偽物の瓶のパターンを判別する事ができます。

　ブリスターパックの取り出し方は実はこれだけでなく、いくらでも別の取り出し方を考える事ができます。上のような対応表を作り1回の測定で真偽を区別できるのであれば、その取り出し方も正解です。

　ここで大切なのは上の表の取り出し方をどうやって導いたか、その理屈ですよね。詳しく解説します。

解説1：瓶が1つの場合

　一番ミニマムな所から考えてみましょう。今瓶が1番だけとします。1番は1錠単位なので、1錠取り出して重さを計れば真偽を確かめられますよね。1gなら本物、0.9gなら偽物です：

　ところで、小数点の重さを直接扱うと見た目も計算もちょっと面倒です（解説も面倒ww）。そこで考えやすいように錠剤の重さを整数表現に変換してみます。

　例えば重さを10倍すると偽物は9g、本物は10gとなり少し扱いやすくなります。でも錠剤が5錠あるとして全部本物なら50g、3錠だけ本物なら47gなどとなり、悪くはないのですが少し野暮ったさが残ります。

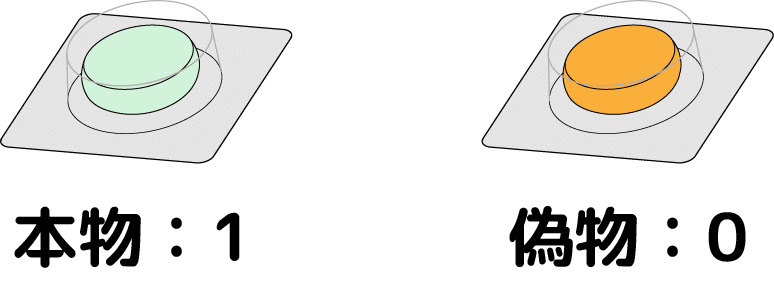
　そこで偽物の錠剤の重さを基準とし、偽物なら0g、本物なら差分の1gとします：

そうすると5錠あって全部本物なら5g、3錠だけなら3g、全部偽物なら0gとなります。これにより「本物の個数＝重さ」となりとても分かりが良くなりますよね。実際の重量に戻すのも、

と計算すれば良いだけです。

　という事で、以後しばらくは測定値の単位も省略して偽物0、本物1として話を進めます。また解説時に混乱しないよう、偽物の錠剤をオレンジにしておきます：

解説2：瓶が2つの場合

　瓶が1番と2番の2つの場合にどうするか？1番の瓶から1単位測定すると測定値は0か1。それに対し2番の瓶は1単位が2錠なので、1単位測定すると0か2が出てくる事になります。そこで両方から1単位ずつ取り出して計測した結果を組み合わせ表にしてみましょう：

　表内の本物の錠数に被りが無いので、共に1単位ずつで大丈夫そうです。ここまでも特に問題は無いですよね。

解説3：瓶が3つの場合

　さて、瓶が3つになると組み合わせは8通りになります。ここで仮に3番の瓶から1単位取り出して、1番2番と共に計測したとします。すると、

上の2つのパターンで同じ「3」が出てきてしまい瓶の真偽を判別できなくなります。これではまずいんです…。

　ここで発想を巡らせます。1番と2番の瓶で最大で3が出てくるのだから、3つ目の瓶では「3より大きい重さが出るようにすれば良い」んじゃないかと。瓶には本物か偽物しか入っていないので、例えば3番の瓶から2単位取り出すと、偽物なら0、本物なら6が出てきます。そうすれば、1番と2番がどのような組み合わせであっても、測定値が6以上か否かで3番瓶の真偽を判定できるわけです：

つまり「他の瓶の合計値よりも重い値が出るように、追加した瓶から単位数を取る」というのがこの問題を解く鍵となる考え方なんです！

　上では3つ目の瓶として3番を使いましたが、1番と2番の最大値である3を越えれば別に4番瓶でも5番瓶からでも構いません。今うまい事4番瓶から1単位取ると「0」か「4」が出る状況がありますので、僕は4番瓶を選択しました。ちょっとくどいですが再度表にします：

0～7まで綺麗に揃っていて無駄が無いのが良い感じです(^-^)

解説4：瓶が4つ、5つの場合

　さらに瓶が増えても考え方は同じです。3瓶の合計の最大値である「7」を越えるように残り3番か5番のどちらかから単位数を取り出せば良いんです。具体的には5番からなら2単位で10、3番からなら3単位で9です。僕は近しい方として3番から3単位を選びました。

　これで1～4番瓶がすべて本物だった場合、7+9=16が出てきますから、5番瓶はそれより大きい単位数にすれば良い。つまり4単位の20でOKとなります。

　という事で、5瓶全部で合計36錠を測定する事になるので、もし全部の瓶が偽物なら「0」、全部本物なら「36」が測定されます。そしてここまでの考え方で測定値に重複が起こらない事はもう確認済みです。実際整数測定値（＝本物の錠剤数）も含めた測定値はこのようになります：

　後はこの測定表から偽物の瓶番号を指定すれば目標達成です。

解説５：取り出し方は無限大

　今回の答えは取り出し方の一例に過ぎません。「他の瓶の合計値よりも重い値が出るように、追加した瓶から単位数を取る」というルールを踏襲すれば、どのような順番で瓶を追加しても上のような判別表が作れます。もし「5番の瓶には1単位しかない」という事であれば、5番を最初の瓶にすればOK。制約次第で色々派生した問題が作れそうですよね。

　ではまた(^-^)/