几帳面な蜂が作る巣の壁の枚数(解説)
問題はこちら:
答え:1482枚
几帳面な蜂達が13層の巣を作った時、その壁の総数は1482枚になります。どう数え上げるかについて、小中学生の皆さんでも計算可能な方法で解説します。
解説1:壁の増え方のパターンを見つけよう
1層目のみの時、壁の枚数は六角形ですから6枚ですよね。では2層目まで拡大した時、壁は何枚増えるか見てみましょう:

2層目の周囲の壁にまずは注目します。上の丸数字にあるように、1層目の赤壁と向い合せとなる赤壁が1枚あり、その間を埋めるように青壁が2枚できています。赤1枚青2枚というセットが6つ分あるので、2層目の周囲の壁は3×6=18枚です。
一方部屋を区切る灰色の壁は6枚です。これは2層目の部屋数と一致しますよね。と言う事で2層目で増えたのは18+6=24枚であるのがわかりました。
次に3層目まで拡張した時の壁の増分を見てみましょう:
2層目の赤い壁と対となる赤壁がやっぱり1枚できています。また青壁と対となる壁も2枚できています。そしてその間を埋めるように緑の壁が左右に計2枚。この赤1青2緑2=5枚のセットが6セット。ここから3層目の周囲の壁は5×6=30枚と分かります。
部屋を区切る灰色の壁は3層目の部屋数と同数になります。その部屋数は2層目の部屋数より6部屋増えます。よって6+6=12部屋。ですから灰色の壁も12枚で、3層目の増分は30+12=42枚となります。
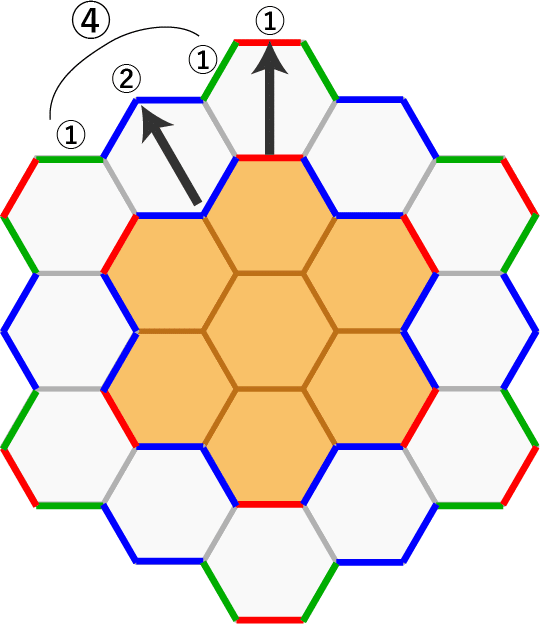
増分のルールを確認するため、さらに4層目も見ておきましょう:

ここまで来ると全部屋描くと目がチカチカするのでww、6分の1の所だけ描きます。4層目でも3層目の赤壁と対となる赤壁が1枚できます。そして、3層目の青と緑の軽4枚の壁に対応する対もあり、残る間を埋める形で黄色い壁がやはり左右に計2枚増えます。赤1、青緑で4枚、そして黄色2で合計7枚。これが1セットで6倍あるので、4層目の周囲の壁は42枚と分かります。
部屋同士を区切る灰色の壁は部屋数と一緒なのでした。これも3層目から6部屋増えるので18枚です。つまり4層目で増えた分は42+18=60枚となります。
さて、増分のルールが分かりましたでしょうか?
各層の周囲の壁は、前の層の周囲の壁数に対しその間を埋める12枚の壁がプラスされます。一方部屋を仕切る壁は1層目は0枚ですが、2層目は6枚、3層目は12枚と6枚ずつ増えています。これら各層の増分を表にすると、

このようになります。まとめると単純なルールになっているのが良く分かりますよね。そして周囲壁と仕切り壁の合計枚数を見ると、1層増えるごとに18枚増えている事も読み取れます。ここから5層目、6層目の壁の枚数も逐次的に求められますね。
今回几帳面な蜂達は13層まで巣を拡大したので、合計欄を13層目まで埋めていって、それを全部足してももちろん構いません。でも、少し計算を工夫してみましょう。
13層目の増分は合計何枚か?表を見ると、1層目は6枚で、以後1層増える毎に18枚増えるので、13層目では6+(12×18)=222枚の壁が増えると計算できます。13層×18枚ではなくて、12層×18枚なのに注意です。ちなみに12層目は6+(11*18)=204枚です。つまり壁の総数をSとすると、

と表せます。
同じ数を足していってできる数字の和を求める簡単な方法は「足し算の順序をひっくり返して各項毎に足す」です。これは数学者のガウスが少年時代に思い付いた方法として有名ですよね。実際にやってみましょう:

上下を足すとすべての項が228となり、それが13項出てきます。ですから下の合計は228×13=2964です。ただこれはSを2回足しているので2倍の枚数になっています。よって2964を2で割った1482枚が几帳面な蜂達が作った壁の総数となるわけです!
今回は周囲壁と仕切り壁の2つを分けて考えましたが、別のパターンに分けて数える事ももちろんできます。面白いパターン分けがあればぜひ教えて下さい。
解説2:一般式を求めよう
さて、高校生以上の皆さんは一般式をバシッと求められましたでしょうか?色々な方針で導けますが、ここでは解説1の結果を踏まえて導出してみます。
各層の増分は1層目が6枚で、以後18枚ずつ増えるのでした。これは高校数学の言葉で言うなら「初項6、公差18の等差数列の和」となります。式で表すと、
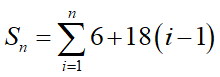
ですね。これを展開して整理すると、

このような一般式を得られます。n=13を入れれば1482枚が瞬時に算出できます!
この一般式から、この蜂の巣は層が増えるごとに2次関数的に数が増加していくというのも分かりますね。ただし各層は前の層に18枚足すだけなので線形な増加です。つまり層が増える毎に蜂がその層を作り切るまでの時間が少しずつ伸びていく…という事です。
深堀:蜂は六角形を意識しているか?
ここからは深堀。今回の深堀は数学ではなく生物学のお話。
蜂の巣には本当に綺麗な六角形の部屋が並んでいますよね。正に自然の芸術です:

では、蜂は六角形の巣を作ろうと意識しているのでしょうか?
これについてネットの情報を調べてみると、次のような見解が多く見受けられます:
「敷き詰め可能で周の長さが同じ正多角形で一番面積が大きいのは正六角形だ。つまり同じ量の材料でより大きな部屋を作れてコスパが良い。だから六角形になるように作っている。」
平面に敷き詰め可能な正多角形は正三角形、正方形そして正六角形しかありません。その周の長さを1とすると、確かに正六角形が一番面積が大きくなります。
ただ、これはおそらく蜂が六角形の部屋を作る理由として十分ではありません。と言いますか、この論法だとおそらく因果関係があべこべじゃないかなと思います。「六角形が面積最大だ→だから蜂は六角形を選んだ」だと、蜂は数学ができる事になってしまいます(^-^;。でも蜂にはきっとそういう高度な計算能力は無いでしょう。…たぶん(^-^;;;
恐らくですが、因果関係は逆です。「六角形がコスパが良いのでそういう巣を作っている」のではなくて、多分蜂は特に計算するわけでもなく本能のままに巣作りをしているうちに、なぜか六角形の部屋が出来上がってしまう。そういう不思議な現象が起きていると考えられます。一般に生態学では生物の行動はエネルギーコストがより安くなるよう最適化されるので、「何らかの行動パターンでコストの安い巣作りをする→六角形になってしまう」という因果関係があると考えられます。
でもじゃあなぜ?なぜそういう行動で六角形の巣になるのか?
これについては僕が調べた限りですが2024年現在も確定的な結論は出ていない模様…(あったらゴメンナサイ…)。説としては今のところ2つの有力な説があるようです。:
A:表面張力説
B:器用な建築家説
表面張力説は、蜂は単純な円形の巣を並べて作ろうとしているのだけど、建築直後の部屋の壁(蜜蝋)が柔らかいため、隣同士の表面張力で六角形に落ち着くという説です。蜂の作用というより物理的な作用によるものだという事ですね:

例えば、でんじろう先生の「はぴエネ!」で六角形のシャボン玉を作る実験がありました。表面張力がある物が互いにくっつくと、互いの空間の面積(体積)を最小にしようとする力が働くため、上の写真のように六角形になります。
同じ事が蜂の巣に作用している場合、蜂は「円形の巣を作ろう」という事だけ考えれば良いので行動が楽(コストが安め)になりますし、また物理的な理屈を鑑みても整合していそうなのですが、実際に蜂が巣を作る様子を調べると、そういう壁の物理的な動き(面積を最小にしようとする動き)が観察されないのだそうです。つまり表面張力説は仮説の域を出ていないと言う事になります。
もう一つのBの器用な建築家説は、蜂が巣作りの際に何らかの建築方式を行っていて、その結果六角形になるというものです。しかも「六角形を作るぞぉ!」とストレートに動いているのではなくて、もっと単純な建築ルール(行動ルール)で巣作りをした結果そうなってしまうという説。
これについて、2024年に神戸大学、山口大学そして関西学院大学の共同研究で初期の巣の形成について一つの見解が発表されました:
論文によると、蜂の巣作りの初期段階の行動には巣の資材を盛り付ける「アタッカー」と盛り付けを取り除く「エクスカベーター」という2種類の行動ルールがあるようで、それにより蜂の巣の基盤となる特徴的な構造が自ずと出来上がるとの事。そういう局所的な行動によって大きなパターン構造物ができる事を「自己組織化」と言いますが、論文では蜂のそれら行動を単純化した数値モデルを作り、コンピュータシミュレーションを行い自己組織化により基盤の構造が再現できたとしています。
初期段階の後の六角形構造ができる本質的な理由は器用な建築家説でも未だ結論が出ていないようですが(あったらゴメンナサイ…)、表面張力説が微妙だとすると、先の研究論文とはまた別の単純行動ルールの結果として六角形が出来上がっているのかもしれませんね。
つまり蜂は六角形をはっきりと意識している…というわけでは無さそうです。この自然の不思議、ぜひ真相を知りたいものです。もしより詳しい事をご存じな先生がいらっしゃいましたら、是非教えて下さい。
ではまた(^-^)/
