放物線で自キャラを狙う敵を作れ(解説)
問題はこちら:
答え:以下の(v0x,v0y)の方向に投げる
(px,py)を敵キャラから見た自キャラの相対位置とした時、

ただし式中のsは、

敵キャラの位置を原点として、上の式から算出できる方向ベクトルv0=(vx0, vy0)で石を投げ出すと、その時の自キャラの位置(px,py)に当てる事が出来ます(v0の大きさは初速v0)。新人プログラマのさとし君がどうやってこの式を導いたか解説します。
解説1:時間-速度グラフの面積が位置になる
敵キャラは初速v0でとある方向v0に石を投げます。ゲームフィールドは2Dなのでこの方向ベクトルv0は2つの軸方向v0x、v0yに分ける事が出来ます:


2次元な動きを各軸に分解する事で挙動を考えやすくすることができます。
まずはY軸方向の挙動から見て行きましょう。ゲームフィールドには重力が働いています。重力加速度はg(unit/s²)です。Y軸方向の初速v0yで放り投げられた石は単位時間でgだけY軸方向の速度が増します。これをグラフ化してみましょう。横軸に時間、縦軸にY軸方向の速度を取ります:

時刻0の時Y軸方向の初速はy0yなのでそれがY切片になります。後は重力加速度gの大きさで速度が線形に変化していきます。上のグラフから時間tでの速度vyは、

という直線式で表現できる事がわかります。
時間-速度グラフの良い所は、その面積を求めると時間tでの位置Pを得る事ができる点です。面積と言えば積分ですね。上式を時間0~tまでの間で積分すると、

このように高さPyの位置を計算する式を得られます。これは物理を習った方にはお馴染みの投げ上げ運動の式ですね。
一方X軸方向の動きは単調です。石が空中にある間は別の力が加わらないので、初速v0xから速度変化は起こりません。よって時間-速度グラフは時間に対して水平です:

この時間-速度グラフからX軸方向の位置Pxを計算する面積の式は、積分するまでもなく単純な長方形の面積ですから、

である事は明白です。
もう一つ今回の問題では初速v0が予め決まっているという条件があります。ここから、

という関係があるのも忘れてはいけません。これで必要な式が揃いました。これらの式から石を投げる速度ベクトルv0=(V0x, V0y)を求めます。
解説2:連立方程式で(v0x,v0y)を求めよう
ここまでの式を再度眺めてみましょう:

v0x、v0y(投げる方向)、t(時間)が未知の変数で、それ以外は既知です。未知の変数が3つなのに対し式が3本あるので、連立方程式から未知変数の値を定める事が出来ます。
どの未知変数から計算しても良いのですが、1本目と2本目の式から、

と方向ベクトルのXY成分を時刻tで計算できるので、tを求めるようにすると便利そうです。そこで3本目の式の両辺をルートを外す目的で2乗し、そこに上の2本の式を突っ込みます:

展開して整理するとtの4次方程式が出てきました。ただこれは、

と置けば実質sの2次方程式です。そこでsを解の公式で解くと、

ごちゃーっとした解になります。ルートの中を展開してもあまりごちゃ感がかわらないので、まぁこのままで良いでしょう(^-^;
時間tは0以上なので、

です。ここからsは0以上である必要があります。
このtをv0xとv0yの式に代入すれば石を投げる方向ベクトルを算出できます:

これで式は完成!では実際にこれらの式で自キャラに本当に石が当たるか、具体的な数値を入れて試してみましょう。
敵キャラの位置を原点として、自キャラの位置をP(10,-4)にします。また敵キャラが投げる石の初速をv0=14とします。重力加速度は地球といっしょのg=9.8としてみます。これらをsの式に代入すると、自キャラに石が到達するまでの時間tが2つ出てきます:
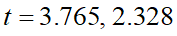
2つ出て来るのはsが2次方程式だからです。ここから方向ベクトルv0=(v0x,v0y)も2つ算出されてきます:

この方向ベクトルでかつその大きさを初速とした石の軌跡を描いてみると…

お見事、自キャラの位置P(10,-4)で2つの放物線が重なって当たっています!
という事でうまく行くことが確認できました。さとし君はこれらの式を使い、放物線で攻撃する敵キャラが投げる石の方向ベクトルを出力するプログラムを作成しました。所が上手く方向ベクトルを求められる事がある一方で、プログラムが正しく動かない、バグる事もあるのがわかりました。
「おかしいな…式は合っているはずなのに…」さとし君は首を傾げます。さて一体何が悪いのか?そしてそれを直すにはどうしたら良いのか?深掘りしてみましょう。

深掘1:自キャラに届く放物線の限界は?
解説で自キャラに当てる放物線が2本描けるのがわかりました。2本出る理由はsが2次方程式で、実数解が2つ存在するからです。これは裏を返せば実数解が存在しない(解が複素数になる)状況もありうるという事です。その条件を洗い出してみましょう。
sの式をもう一度見てみます:

このルートの中が0以上なら実数解が存在します。つまり、
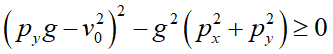
この式を展開してみます:

左辺のべき乗を無くすため、両辺を1/2乗しています。下段右辺は正なのでそのままで良いですが、左辺は括弧の中がプラスにもマイナスにもなりえるので、不等式を検討する場合は絶対値を付ける必要があります。
左辺の絶対値内がプラスの時、

この右辺の括弧の中はマイナスです。一方で左辺は0以上なのでこの式は成立しません。つまり絶対の中はプラスになっていはいけないという事です。
絶対値の中がマイナスの時、

この右辺のルートの中は正なのでこの式は成立します。つまり初速v0が少なくとも右辺の大きさ以上になっていないとsが虚数解になってしまうんですね。感覚的にイメージするなら、自キャラがうーんと離れていたら(=上式の右辺が凄く大きかったら)敵キャラがどう頑張って投げても石が届かないですよね。
この事を考慮に入れて、石の初速v0が自キャラに届く初速に達していなかったら例外処理を走らせるようプログラムを修正したさとし君。所が、まだバグが発生する事がわかりました…。さとし君の苦悩は続きます。
深掘2:例外的な値になる時を考慮しないと…
sの式をもう一度じーっと眺めてみましょう:

この式、重力加速度gが0の時に分母がゼロ、つまりゼロ除算が発生してしまいます。gが0というのは要は無重力のフィールドです。どうやらこのゲームには無重力の世界もあるようです。そのためg=0の時は別の式を立てないといけないんですね。
解説で出てきた面積から導出した位置の式を見てみましょう:

2本目の式にのみgが関わっています。g=0の時pyは単なる直線の式になります。それを3本目の式に代入すると、

シンプルなtの式が出てきます。右辺の分子は敵キャラから自キャラまでの距離ですよね。つまりこれ小学校で習う[距離]/[速度]=[時間]の式です。このtから、

で無重力時の石の方向ベクトルが求まります。ただしtの式の分母にv0があるのに注意です。これがゼロの場合は時間tが無限大に吹っ飛んでしまう(石が静止しているのでいつまで経っても自キャラに当たらない)ため、それも例外としてエラー処理を入れる必要があります。
今度こそはとg=0の特殊な場合、そしてg=0で初速v0も0の場合の特別処理をプログラムに追加したさとし君。しかしテストプレイでまたしてもバグが発覚…。
深掘3:石を投げた瞬間に自キャラに当たる事だってありうる!
重力加速度g>0でかつ有効な初速v0もある、解説で導出した方向ベクトルを求める最後の式を再度ご覧下さい:

この式、√sで割っていますよね。つまり√sがゼロの時は無限大に吹っ飛んでしまうんです。s=0の状況が起こるのか?そして起こる条件は何なのか?
重力加速度gがゼロじゃない時にsの式がゼロになるのは、分子がゼロの時です。つまり、

この式を展開して原因の元を探ってみましょう:

今gはゼロでは無いので、この式が成立するのはpx=py=0の時のみです。相対位置が(0,0)、つまり敵キャラと自キャラの座標がピッタリ重なっている時、sは0になりゼロ除算が起こりバグが発生してしまいます。それを判別して取り除いてあげないとプログラムは暴走してしまうんですね。
涙目になってプログラムを再再再度修正したさとし君。もうバグらないでくれ…。そんなさとし君の願いもむなしく、デバッグ中にさらにバグが発生してしまいました。ここが正念場、頑張れ、さとし君!

深掘4:重力加速度がプラスと誰が言ったかね?
現実の世界では重力加速度の値はプラスです(スカラーとして)。しかし、ゲームの世界では重力が反転する世界だって実現できます。つまりgはマイナス値にもなりうるんです。実際プランナーはゲームを面白くしようとgにマイナスの値を入れてしまったんです。そしてさとし君のプログラムの所でゲームが暴走してしまいました…。
さとし君は仕様書を改めて見直しました。確かに重力加速度の表記はありますが、それが地面方向であるとは書かれていません。つまりg=0だけじゃなくg<0の時も考慮しないといけなかったんです。
g<0の時にヤバいのはどこか?それは初速v0の妥当性を調べるこの式です:

g>0の時は問題無いこの式ですが、g<0の時はルートの中がマイナスになってしまいますよね。これはプログラムの計算では認められないので、ここでプログラムが暴走してしまったんです。
この条件式を導いた所を再検討しなければなりません。深堀1で導いたsが実数解になる条件式を再掲します:

g<0があるとなると、この不等式の展開は致命的なミスを犯しています。右辺のg²を1/2乗して下段にした時、これは絶対値を付けないといけないんです。つまり正しくは、

です。
g<0の時、上の式のgの絶対値を外すと、

となります。これで左辺の絶対値内がプラスとマイナスで場合分けします。プラスの場合、

下段右辺が常にマイナスなので成立しません。マイナスの場合は、

今度は下段ルート内がプラス(gがマイナスで且つ括弧の中もマイナス)ですから成立しています。g<0の時は初速v0の条件式をこちらの式で判定しないといけなかったんですね。
度重なる不具合発生にすっかり落ち込んでいたものの、原因を見つけてg<0の時の処理をプログラムに書き足したさとし君。どうやらこれでバグを潰し切れたようです。「開発中にバグが見つかるのはありがたい事さ。めげずによく頑張って直したね」先輩プログラマが優しく慰めてくれて、少し気持ちが安らいださとし君でした。さ、明日もプログラムがあるぞ。頑張れ、さとし君!

さていかがだったでしょうか?新人プログラマのさとし君の苦悩を見て分かるように、僕らゲームプログラマは様々な状況を想定してバグ(プログラムの暴走)が起こらないように例外処理をコード内に施します。石を放物線状に飛ばしてターゲットに当てるだけでも実は大変なんです。実際のゲームはもっと複雑で多様な条件が折り重なりますし、開発途中で仕様が変更される事も沢山あります。
例えば今回さとし君が泣きながら頑張って修正を繰り返したコード(アルゴリズム)は、重力が真下もしくは真上方向に限定されています。もし仕様が変わって重力が斜めを向く場合もあるとしたら?さとし君のコードは残念ながらそれに対応できません。その仕様変更を聞かされたさとし君は憤怒するかもしれませんね。「そんなの聞いてない!初めから言ってくれれば…!」って…。
でも、実は実際のゲームプログラムの現場ではそういう仕様変更は日常茶飯事に発生します。工業的なプログラムだと仕様を厳密に決めてからコードを書きますが、作りながらより面白くなる仕様を模索するのがゲーム制作なので、どうしても仕様変更が多発してしまうんです。だから僕らは仕様変更は起こるものだという前提で、起こりそうな変更を「予知」してちゃんと対応できるように予めコードに柔軟性を確保しておきます。プランナーから仕様を聞かされた時にそれを鵜呑みにせず「あ、多分ここは拡張しないと後でヤバい事になるな…」と予知する。この予知能力の有無が新人とベテランゲームプログラマの違いの一つと言えるかもしれません。
プログラムを正しく動かす事は思っている以上に大変ですが、うまく動いた時の快感は格別です。そのトキメキを毎日味わえるゲームプログラムが、僕は大好きです。
ではまた(^-^)/
