ドーナツをくりぬいて同じ形のドーナツを作る（解説）

　問題はこちら：

答え：以下の式で求まる半径で分ける

　元のドーナツを上式で求めた半径xで分割すると、分けたドーナツは同じ形、すなわち相似になります。この式を求める方法を解説します。

解説：内円と外円の比を同じにする

　2Dのドーナツは内円と外円の半径の比が同じであれば相似と言えます。今元のドーナツの内円の半径はr、外円はR、そして2つのドーナツに分ける中間円の半径はxですから、分けた後の2つのドーナツの半径はそれぞれ以下のようになります：

　これらが相似の時、次の比が成り立ちます：

これをxについて解くと、

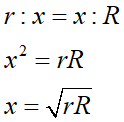
答えの式が導けます。

　r=1としてRの大きさを変えるとxの値は勿論変わります。つまり外円、内円の比率によって中間円の半径の比も変わると言う事です。どうやら謎解きゲームの答えは必ずしも正しいとは言えないようです。

　該当の謎解きゲームは幅広いプレイヤーに気軽に楽しんで貰えるように、それこそ小学生でも先に進めるように非常に丁寧な表現と適切な難易度の問題で構成されています。僕の大好きなゲームの一つです。今回の問題も「どういう風に切り取ると同じ形になるか？」というのが本来でした。なのでそこにある半径の定数値はあくまでも単に目安として示した、という事なんだろうと想像します。僕もゲームプログラマなので、この辺りの表現の塩梅は理解できます。

深堀1：謎解きクイズの答えになるrとRは？

　ここからはちょっと深堀です。この問題の元となった謎解きクイズで示されていた分け方の定数は、要約すると「元のドーナツの厚みを2:1に分ける」というものでした。これが必ずしも真ではない事は前述した通りです。

　では、謎解きクイズの答えがちゃんと正解となるrとRがいくつなのか、逆に求めてみましょう：

　元のドーナツを上図のように2:1に分けます。一つ分の長さをaとしましょう。ここからRとxをrとaで表現してみます：

このまま解いても良いのですが、今欲しいのはrに対するRの長さの比なので、簡単のためr=1としてしまいます。こうしても本質は変わりません：

xは今回の問題で求めた√rRでなければ相似にならないため、

という制約があります。左辺のxに②式を代入して、

①式から、

これを先の式に代入して整理すると、

綺麗に因数分解できて、R=1と4が分かります。ただR=1はr=1と同じ半径になるのでNG。よって採用するのはR=4で、r:R=1:4の時謎解きゲームの解答は正しくなります。

深堀2：偏心ドーナツで相似を作れるか？

　この問題についてあれこれ考えている時、ふと「あれ？切り取る円をずらしてもこれ相似っぽくなりそう…」というのに気が付きました。

　切り取る中間円の中心をドーナツの中心からずらした場合、2つに分かれたドーナツはどちらも真ん中の円が偏ってしまいます：

これを偏心ドーナツと呼ぶ事にします。パッと見た感じでは、中間円の半径とその中心点の位置をうまく調整すると相似に出来そうな感じはします。果たしてそれは可能なのでしょうか？

　精査するため、外円の半径と中心からのずれを文字で表してみます：

　元のドーナツの中心に対して、切り取る中間円の中心点のずれ幅をaとすると、R、r、xとの関係は上図のようになります。

　ここで矢印の先の2つの偏心ドーナツのずれ幅aに注目です。これらが相似になるには、少なくとも外円の半径に対する内円のずれ幅aの割合が双方で同じにならないといけません。これが異なると内円がどのような半径でも相似になり様がないですよね。

　上右図から半径とずれ幅aを比で表すと：

こうなります。今偏心がある前提なのでaが0より大きいため、これを満たすには、x=Rでなければなりません。しかしその場合切り取り範囲が大円外に飛び出してしまうためNGです。

　つまり、偏心ドーナツは相似に出来ない事がわかります。

　社会には一見正しそうに見える事や、曖昧に表現されている事が沢山あります。そういう状況を観察し整理して、可能であれば数式におこしてみる。それによりその状況の真偽が明らかになったり、より明確になったりします。これもまた数学の力の一つですよね。

ではまた(^-^)/