迷路を作る内壁は何枚必要？（解説）

問題はこちら：

答え：2401枚

　50×50のマス目に迷路を描いた時、内壁は2401枚必要になります。これは問題の条件を満たす迷路であればどのようなパターンを作っても一緒です。壁の数を数える考え方は沢山ありますが、その一つを解説します。

解説：壁を1枚壊すと迷路が広がる

　いきなり50×50で考えるとパターンが無限に広がってしまい大変です。そこで非常に小さい迷路で考えてみましょう。

　一番小さい迷路は1マスの迷路です：

スタートとゴールが同じでもはや迷う事も無い迷路ですw。この迷路の内壁は0枚ですね。

　この1マス迷路の隣に部屋を一つくっ付けます：

例えば上にくっつけた部屋を有効にするには、接している壁を1枚壊せば良いですよね：

「1部屋増やしたら壁を1枚壊す」これ、ポイントです。

　ゴールの左にも部屋をくっつけてみましょう：

そして共有している壁を1枚壊します：

やはり「1部屋増やしたら壁を1枚壊す」が成り立っています。この部屋の増やし方をするとループが起こる事もないですし、隔離部屋ができる事もありません。

　そうなんです、今回のルールに従った迷路というのは、上のように「増やした部屋数と壊して無くした壁の枚数が同じ」なんですね。1部屋で0壁、2部屋で1壁、3部屋で2壁、4部屋で3壁…という関係です。

　この関係がわかればもう数式を立てられます。方眼紙の縦をMマス、横をNマスとします。マスの総数Tは、

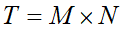
です。この部屋数と壊す壁の枚数Dには以下の関係があるわけです：

　この縦M横Nマスの方眼紙の部屋に設置可能な内壁の総数をSとします。このSから壊した壁の枚数Dを引けば、残りが迷路を作る内壁の枚数Wになります：

　Sの枚数は縦壁と横壁に分けると考えやすいです：

縦壁は1列にM枚あります。その列はN-1列あるので、竪壁の総数は、

と計算出来ます。同じように横壁は1行がN枚あり、それが縦にM-1行あるので、

同じような式で求められます。以上から設置可能な内壁総数Sは、

と縦横のマス数で表現できるのがわかります。これを迷路の内壁の総数Wの式に代入すると、

方眼紙の縦横マス数から迷路を形作る内壁の枚数を計算する式が出来ました！各辺のマス数から1引いた数を掛け合わせる…そうこれは「交点の数」なんですね！

　今回方眼紙の縦横は50マスです。上式のM、Nにそれぞれ50を入れると、

2401枚である事が分かりました。

深掘：迷路を作る超シンプルなアルゴリズム「棒倒し法」

　ここからは深堀なお話。
　迷路をせっせと描いていた少年時代から、高校生くらいの時にPC（PC9821）を買いました。そこでC++を知って、グラフィック関数を使って画面に線を引けるようになりました。プログラムで線を描けるようになったら…そう迷路を作図です。

　迷路を作成するアルゴリズムは色々とありますが、昔から良く用いられているのが「棒倒し法」です。完全なランダムの迷路になってしまうので少し面白味は欠けるのですが、比較的簡単に実装できます。

　棒倒し法の手順を見てみましょう。まず縦Mマス、横Nマスの方眼紙を想定します。棒倒し法で着目するのは格子の交点です：

　左上の1番目の交点に棒なり鉛筆なりを立てて、上下左右のどちらかの方向にパタっと倒します。倒れた方向に線を引くと壁が1枚描けます。

　次に一つ右の交点に移り、同じ棒倒しをするのですが、もし倒れた先に既に壁が描かれている場合は再抽選します：

同様に最上段の右端まで同じ棒倒し作業を続けていきます：

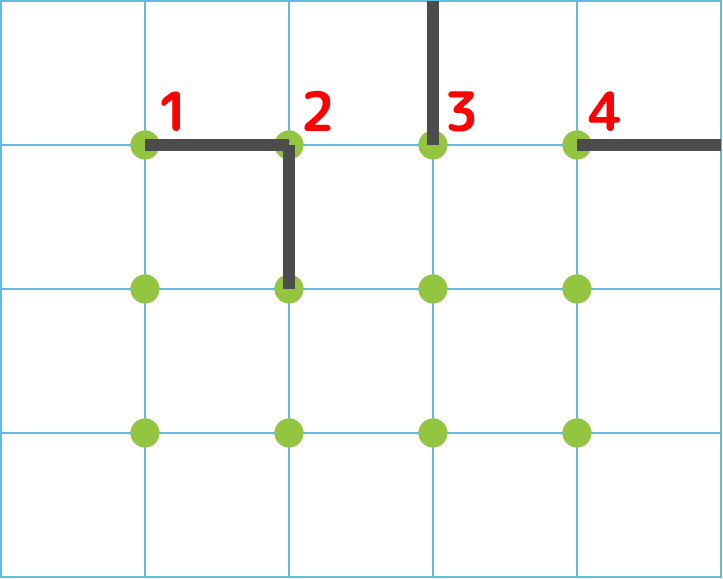
　最上段が終わったら同じ事を2行目にも適用します。ただし2行目は上の壁を選択から外します：

上の壁を入れてしまうと隔離部屋が出来てしまう事があり、ゴールにたどり着けない迷路ができてしまう事があるためです。以上を最下段の右端まで続けて行くと今回の問題の条件にあった「閉鎖個所が無くループもしない」迷路が出来上がります。

　…という事で、実際に作ってみたいですよね～。そこで上の棒倒しアルゴリズムで実際に動くプログラムをこちらで公開してみました：

　こちらは「マルペケの徒然なるプログラムのお話」という僕が書いている別のマガジンでの記事です。プログラムに関係する話を思いついた時にブログとしてアップしています。色々やっていますのでご興味がある方はつらつらとお読み頂けると嬉しいです。

　記事の最後にあるコードをコピペしてテキストファイル（maze.py）として保存してダブルクリックするか、コマンドプロンプト上から、

python ./maze.py

とすると迷路が描かれたウィンドウが表示されます：

凄く短いコードで簡単に迷路が作れるので面白いですよ。是非試してみて下さい。

深掘2：立方体の迷路の内壁

　迷路は普通2Dですが、正方形の方眼紙の代わりに立方体を使えば3Dの迷路も考えられますよね。ただ3D迷路は俯瞰出来ないのと人の認知を超えてしまうため、あんまり面白くないというのが欠点なんですが(^-^;。

　立方体を組み合わせた3D迷路の内壁の枚数も今回の「部屋をくっつけて共有する壁を壊す」という考え方で求める事が出来ます。

　XYZ方向に立方体を敷き詰めて大きな直方体を作るとします。各軸方向のマス数をそれぞれNx、Ny、Nzとすると、立方体の部屋の総数は、

です。

　1部屋のみから始めて、隣に1つ部屋を増やすと壊す壁が1つ増える。この発想は一緒です。よって壊す壁の総数Dは、

となります。内壁の総数Sは、例えばX軸を法線に持つ壁（YZ平面に平行な壁）は一列NyNz枚でそれがNx-1列ある、この法則は他の軸でも同様なので、

こう表せます。よって迷路を作る内壁の総数Wは、

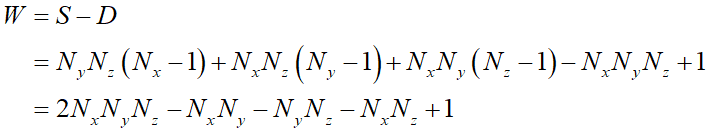
こういう数式で計算できます。この式、何か因数分解できて綺麗になるのかなぁとあれこれ検討してみたのですが、あまり綺麗にならないようで、2Dの時のようなトキメキはそんなにありません(^-^;。強いて挙げるなら、

こういう式の形にすると意味合いはくみ取れます。右辺第1項の(Nx-1)(Ny-1)は2Dの内壁の枚数です。これにNzが掛け算されているので、これは「Z軸方向の各層での内壁枚数」になっています。ただし2Dの迷路をZ軸方向に重ねても天井が無いので、それとは別に天井を張る必要があります。ループを避けるには天井に一つだけ穴が開いている必要があります。よって天井を構成する内壁はNxNy-1枚になります。天井の枚数はNz-1なのでそれを掛けると天井を構成する内壁の総数になります。両者を足すと総内壁数になるわけです。

終わりに

　今回は迷路の内壁のお話でした。何かを数え上げる時に漠然と数えると大変ですしミスも出ます。そこにルールがあるのなら、何らかの数学的な感覚で上手に数え上げられるかもしれません。そういうのを見つける事で色々な最適化ができ、それは実社会でも様々な形で応用されています。例えば計算上の数と実際の数が違えば、そこに何かミスがあると見つける事もできるわけです。皆さんも身の回りにある数え上げられそうな物を見つけて「数学的に数える方法」を模索してみて下さい。

ではまた(^-^)/