道をスムーズに繋ごう(解説)
問題はこちら:
答え:以下の式

問題の道をスムーズに繋ぐ経路は上式で計算できます。式内の係数をどう計算するか解説します。
解説:スムーズは「微分」で
今回の接続道の経路は以下の式で計算するとしました:

問題の条件を満たす係数a~fを求めるのが目的です。
まず曲線はt=0の時にS(0,0)を通るのでt=0を代入してみます:

係数cとfがそれぞれゼロなのがわかりました。
t=1の時曲線はG(6,4)を通ります。同様にして、

aとbそしてdとeの関係が出てきました。
試しにc=f=0且つ上の足し算の関係を満たすように適当な係数を入れてグラフをいくつか描いて見ると、

カーブ具合は異なりますが、どれもちゃんとSとGを通っていますよね。この多様な曲線の中に「両端で直線道とスムーズに繋がっている」ものがあるはずです。
問題ではSの所で右向き(1,0)の、Gの所で左斜め上(-1,1)の直線がそれぞれ伸びています。この曲線がそれら直線道とスムーズに繋がるには、曲線上のS、Gでの接線が直線の方向と一致している必要があります。
曲線の接線(傾き)はその点で曲線を微分すると求まります。傾きと言うと高校数学では、

このようにxの増分に対するyの増分と表現しているのをよく見ますが、今回はx、yそれぞれが媒介変数tで表現されています。tがちょびっと増えた時にxとyがそれぞれ同時にどのくらい動くか?とイメージするのがコツです。つまり、

これが任意のtでの接線の方向ベクトル(x'(t), y'(t))になるんですね。
t=0、すなわち点Sでの方向ベクトルは(1,0)なので、上式にこう当てはめたくなります:

ですが、ここで注意が一つあります。(1,0)はあくまでも「直線道路の方向」なので、その大きさが曲線の接線ベクトルと同じとは限りません。と言うか曲線自体不明なのですからそれは普通一致しません。
そこで点Sにおける曲線の方向ベクトルの大きさを「不定」として(s, 0)と定義し直し、このsも求める係数としてしまいます。すなわち、

と式を立てられて、

bはsと等しく、eがゼロである事が分かりました。
同じ事は点Gでも言えます。Gの直線道路の方向は(-1,1)ですが、曲線の接線の大きさはやはり未定です。よってこれも(-g, g)と再定義します。微分式にt=1を代入して、

係数の関係式を得られます。
この段階で未知係数はa,b,d,e,s,gの6つ。4つの微分式と最初の方で求めた、

式が計6本あるので連立方程式を解けば各係数がすべて一意に求まります。どう解いても良いのですが、例えばe=0から、

dが得られます。dが分かれば、
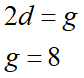
が求まります。後は、

ここから、

が導けます。これですべての係数が求まりました!道をスムーズに繋げる接続道の式は、

となる事がわかりました。実際にこの係数で接続道のグラフを描いてみると、
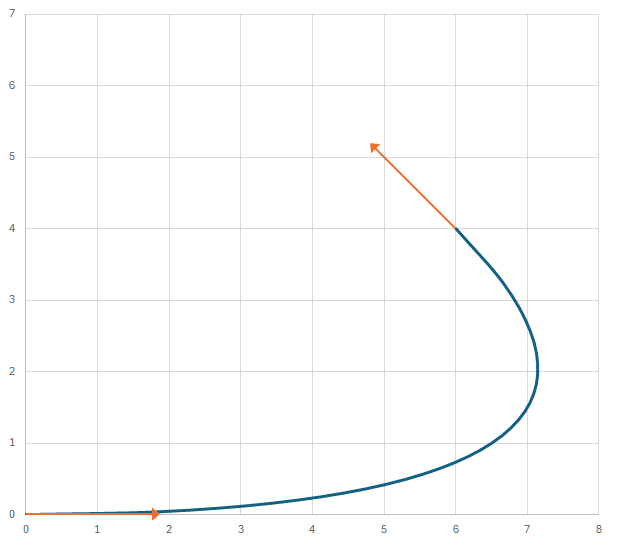
オレンジの直線道の方向に曲線がスムーズに繋がっています。ばっちりです(^-^)
ちなみに、この曲線は「2次のスプライン曲線」と呼ばれています。2点の接線方向に対して曲線がスムーズに繋がるので工学やコンピュータグラフィックスなど色々な場面で利用されています。皆さんがPCで目にしている文字、いわゆる「フォント」も実は2次のスプライン曲線で描かれているんですよ。
深掘1:道路の「運転しやすさ」
さて、こうして接続道の経路が求まったわけですが、果たしてこのカーブに沿って本当に工事を進めて良いのでしょうか?見た目にはスムーズに繋がっているので良さそうに見えますが、実はこの道路、あまり運転しやすい道では無いんです。
「運転しやすい」というのは随分と曖昧な表現ですよね。何をもって運転しやすさを評価するか?これは色々な考え方がありますが、一つの観点として「運転時のハンドルの動かし具合」を評価する見方があります。
サーキットのようにハンドルを激しく動かすコースは明らかに運転し辛いですよね。反対に直線道路はハンドルを動かす必要が無いので運転しやすい道です。つまりこの評価基準では、出来る限りハンドルを動かさない道が理想となります。
ではカーブを曲がる際に運転者はどのくらいハンドルを動かすことになるのか?それを求めるには「曲率」という概念を知る必要があります:
滑らかな曲線がある時、曲線上のある点の曲がり具合にフィットする円を想定できます。その円の半径の事を「曲率半径」と言います:

カーブがきつくなる程この曲率半径が小さくなるのは感覚的にわかりますよね。曲率半径はこのように概念的には分かり良いのですが、直線だと半径が無限大になってしまうため数学的に少し扱いにくい面もあります。そこで曲率半径の逆数を取って直線でも曲線でも値が出るようにします。この曲率半径の逆数が曲率と定義されています。
今回のようなxとyが媒介変数tで表される曲線の曲率ρを求める式は解析的に解かれていまして、以下のようになります:

式中のx'はxの1階微分、x''は2階微分を表します。yについても同様です。ぱっと見はうんざりしますが(^-^;、微分式のみで構成されているので実は案外取り扱いやすい式です。
また曲率の定義から曲率半径は、

と逆数で計算出来てしまいます。便利(^-^)。
今回求めた接続道の曲率式を求めると、途中の展開は冗長なので省略しますが(微分式を代入して整理するだけです)、

となりました。これを横軸がt、縦軸が曲率ρのグラフに描くと、

こんなうねった曲率になるのがわかりました。
曲率がうねっているという事は、曲率半径が常に変化し続けているという事です。しかもピークで値が急激に下がるので、ここでハンドルを逆方向に素早く切り替える操作になってしまいます。急ハンドルは事故の元ですから、こういうカーブを一般道路に採用するのは危険です。
このようにカーブの曲率をグラフにすると、そのカーブがどのような性質を持っているか具体的に見えてきます。少なくとも今回の計画で求めたスムーズに繋がった接続道は、運転者にとってあまり好ましいカーブをしているとは言い難いようです。どうやら工事計画の見直しが必要のようですね(-_-;
深掘2:円に沿ったカーブのみで接続するのは理想のようで実は危ない
カーブでハンドルを動かすと運転が難しくなる。であればカーブでハンドルを動かさなければ良いのでは?そう発想するのは自然な事です。
ハンドルを一定の角度で固定して車を運転すると円弧を描きます。逆に言えば円弧のカーブはハンドルを動かさなくて良い理想のカーブと言えます。しかも円弧(円)はぐるっと回って元に戻る曲線ですからあらゆる方向の接線が存在しています。つまりどんな直線ともスムーズにつなげられるポテンシャルを持っています。円弧最高~。
所がです。実は円弧のみで直線道路と接続すると危険な個所が存在してしまいます。それはカーブの最初と最後です。
例えば次のような円弧のカーブがあったとしましょう:
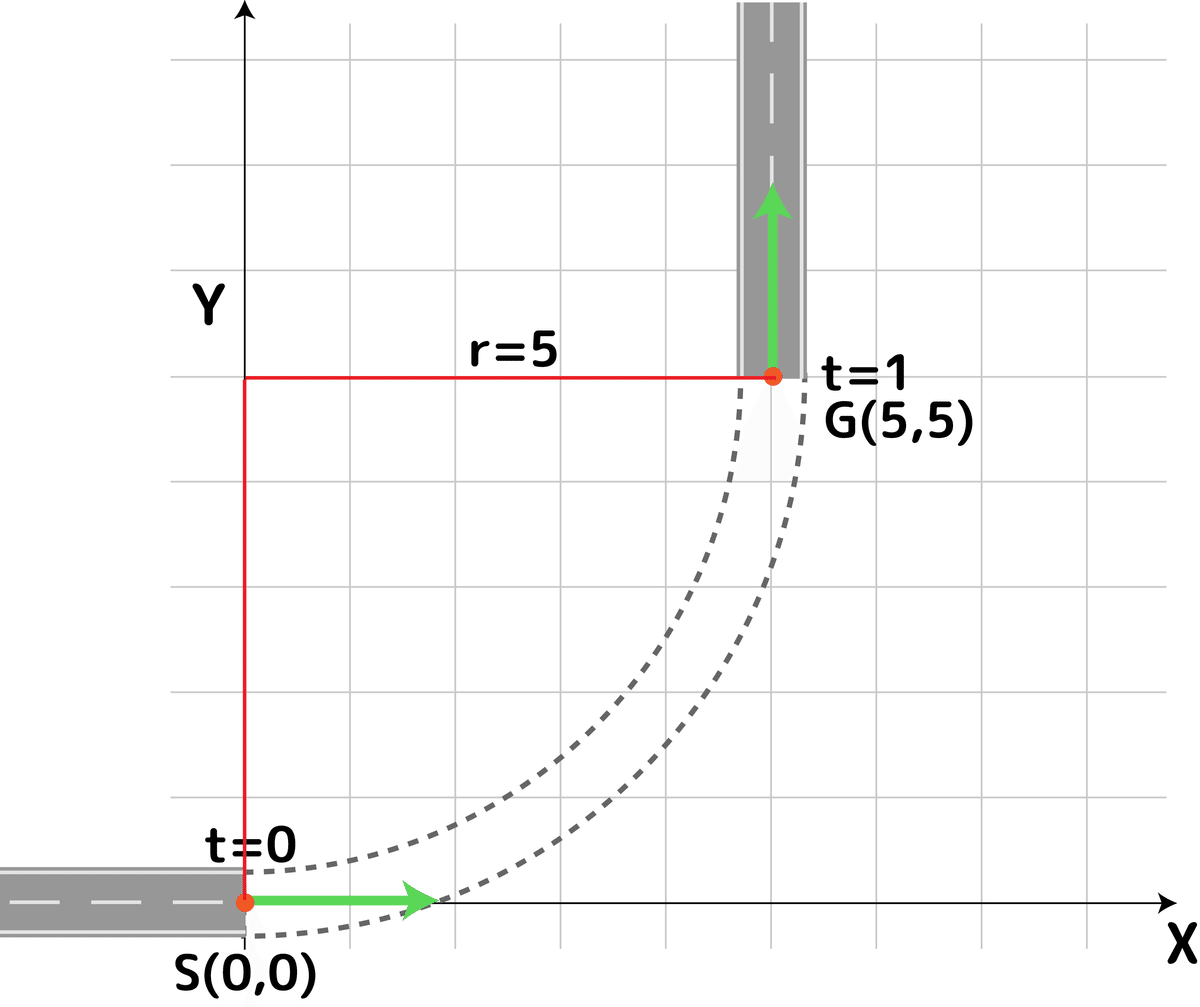
左下と右上の直線道路が曲率半径5の円弧の道路で接続されています。SとGそれぞれで円の接線ベクトルは直線道路の方向ベクトルと一致しているのでスムーズに繋がってもいます。これのどこが危険なのか?それはこの道路の曲率をグラフにすると分かります:

便宜上Sの前のtをマイナス、Gの後はt>1としています。t<0とt>1の直線道路はカーブしていないので曲率は0です。しかしt=0の所でいきなり曲率がρ=1/5=0.2に不連続に変わっています。
曲率が不連続という事は、そこで曲率半径が不連続に変化している事になります。つまりそこでハンドルを瞬時にカーブに合わせなければならない事を意味します。急ハンドルは事故の元の観点で言えば、これは最悪です。急激なハンドル操作は搭乗者に非常に大きい横方向のGを与えます。カーブがきつい場合はむち打ちになりかねません。またタイヤが瞬時に斜めを向くため車が横滑りする危険も生じます。カーブで横滑りすると対向車線にはみ出すわけで…。想像するだけで恐ろしいです。もちろん車にかかる負担も大きいです。
車がカーブの軌道に乗れば円弧は安定なのですが、接続点にある欠点は決定的で、このままではとても安全なカーブとは言えません。微分的に見てスムーズに繋がっているように見えても、曲率で見ると実は不連続になっている。ぱっと見では分からない道路の危険性を曲率のグラフはあぶりだしてくれるんですね。
深掘3:クロソイド曲線+円弧の合わせ技
さて、では運転者に優しいカーブとはいったい何なのか?一概に最適解がある訳では無いのですが、多くの道路で採用されているのが「クロソイド曲線」と呼ばれる特別な性質を持った曲線です:
直線道路からカーブに差し掛かった時、いやでもハンドルは動かさないといけません。この時瞬時に動かす必要があるのが円弧のカーブでした。そうではなくより自然なハンドル操作は「徐々にハンドルを切っていく」ではないでしょうか?そのようなハンドル操作を想定した曲線がクロソイド曲線なんです。
クロソイド曲線は下のような渦巻き型の曲線です:

左下からスタートして、ハンドルを徐々に左に回していくと、あ~なんかこんな曲線を描きそうってイメージできますよね。
もう少し数学寄りに言うと、車が進んだ距離Lに比例して曲率ρが一定に増加していくとクロソイド曲線になります。距離と曲率の関係を式で書くと:

です。αは比例定数で、ハンドルを回す速さと対応しています。
上の式から横軸を移動距離L、縦軸を曲率ρとしてクロソイド曲線の曲率グラフを描くと、

このように直線になります。曲率が増加しているので進むほどにハンドル角度は大きくなっていくわけですが、重要なのは「ハンドルを回す速さが一定」という性質です。つまり急ハンドルを切っていないんですね。
クロソイド曲線は渦巻きなのであらゆる方向の接線が存在します。つまり直線道路とスムーズに繋げられるポテンシャルも持っています。素晴らしい。
今回の問題の直線道路をクロソイド曲線で連結するとこんな感じになります:

しかし1本のクロソイド曲線で強引に繋ぐと下図のように終点で不連続が発生してしまいます:

これは円弧と同様でハンドルを瞬間的に戻す危険な繋ぎ方です。そこでカーブの途中で今度はハンドルを逆方向に一定速度で戻す2本目のクロソイド曲線を繋げます:
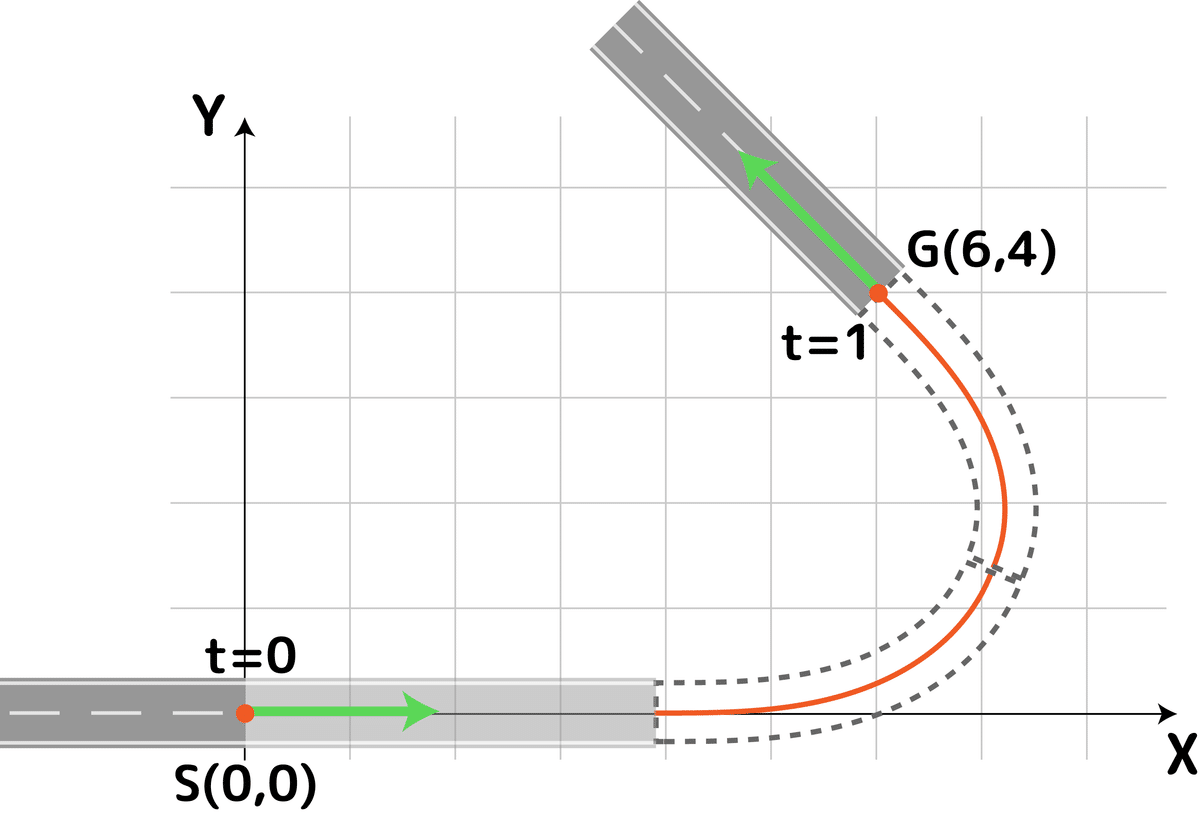
後半のクロソイド曲線に繋げるために始点の直線を伸ばす必要があります。このカーブの曲率グラフのはこんな感じになります:

これで終点の所でハンドルを戻し切った時に丁度直線道路になる接続ができました。かなり理想的ですよね。
ただ上のグラフだとカーブが一番きつくなったL=0.7辺りの所で逆ハンドルを切る操作が入ります。左に回して回して回して…はい右回転開始!っという感じ。極端では無いもののそのタイミングが急にやって来るので、運転者が戸惑う可能性があります。
そこで実際の多くの道路では「最初はクロソイド曲線で、ある程度進んだら円弧で、その後またクロソイド曲線で戻す」という合わせ技カーブが採用されています:

青い道路がクロソイド曲線、オレンジが円弧のカーブです。もちろんクロソイド曲線と円弧の接続点は同じ接線ベクトルになっています。何となく「あっ、地図で見る道路のカーブって確かにこんな感じかも」って気がしませんか(^-^)
この曲線を複合した道路の曲率グラフを描いてみましょう:

先程の尖がった曲率グラフの頂きが平らになりました。この平らな所が円弧のカーブの部分です。
この道路を運転者の操作目線でなぞると、まず直線からカーブに差し掛かったらハンドルを一定の速度で左に回し始めます。ある程度進むと円弧に入り、ハンドルは固定のままでOKになります。この円弧を運転している間で運転者は「次に来るハンドルを戻す準備時間」を得る事ができるんです。そしてカーブが緩みだす後半のクロソイド曲線からはハンドルを逆方向にまた一定速度で戻します。カーブが終わって直線になった時には、ハンドルも自然と無回転の位置に戻っています。
このハンドル操作は実に自然で運転しやすいですし、急激なハンドル操作が無いため、運転者だけでなく搭乗者や車にも負担が少ないのが感覚的にわかりますよね。このようにクロソイド曲線+円弧の合わせ技の道路は多くの利点を持つ事から、一般道や高速道路、鉄道などにも採用されています。
2つの断絶した道を繋ぐ経路は無数にあります。その中で今回の問題は「スムーズに繋ぐ」という側面で経路を導きました。しかしそこに「運転しやすさ」や「安全性」というファクターをさらに加える事で、人類はクロソイド曲線というさらに理想的な曲線を見つける事ができたんです。こういう所に数学の便利さと凄みを感じますよね!
ではまた(^-^)/
