ピラミッドを包む円の半径は?(解説)
問題はこちら:
答え:以下の式
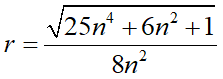
n段の正方形で構成されている高さ1のピラミッドを包む外接円の半径は上式で算出する事ができます。解法は多分色々あると予想しますが、ここでは僕が見つけた2つの方法を解説します。
解法1:連立方程式を使って解く
まずは以下の図をご覧下さい:

n段で高さ1のピラミッドを覆う外接円には中心点Oがもちろんあります。ピラミッドは左右に線対称なので、中心点Oは赤線で示したピラミッドの中心線上のどこかにあります。ピラミッドは一番上のブロックの上隅と底面の下隅でそれぞれ接しています。ここから上図のように中心線上にある中心Oから円周との接点までが円の半径rとなります。
図をじーっと見ていると、rを含む直角三角形が2つあるのがわかります:

下の直角三角形の高さをhとします。その底辺は1/2です。ピラミッドを構成する正方形の一辺の長さは1/nであり、ピラミッドの最下段には正方形がn個並んでいるので、その長さはnによらず1になります。下の直角三角形の底面は丁度その半分なので1/2です。ここからピタゴラスの定理を用いてrを求める式ができます:

一方で上の細い直角三角形の高さは、ピラミッドの高さが1で下の直角三角形の高さがhなので1-hです。上辺は正方形の辺の半分なので1/2n。ここから同じくピタゴラスの定理で2本目の式を立てられます:

この2本の式を連立方程式で解けば半径rが求まります。hを消してrを残しても勿論解けますが計算がやや大変になるので、逆に一旦r²を消してhを求めます:

このhを上のr²の式に入れて整理すると、

外接円の半径rをnで表す式が導けました。
解法2:弦を利用して解く
僕が最初に見つけたのはこちらの解法です。解法1はその後で気付きました。解法1よりもやや冗長ですが、別解として解説します。
中心点から弦への垂線は弦の中点を通る

仮に中心点があるとして、ピラミッドと円周との接点まで伸ばした赤線分が半径rです。ここで赤線と円周との交点を結んで弦を作ります:
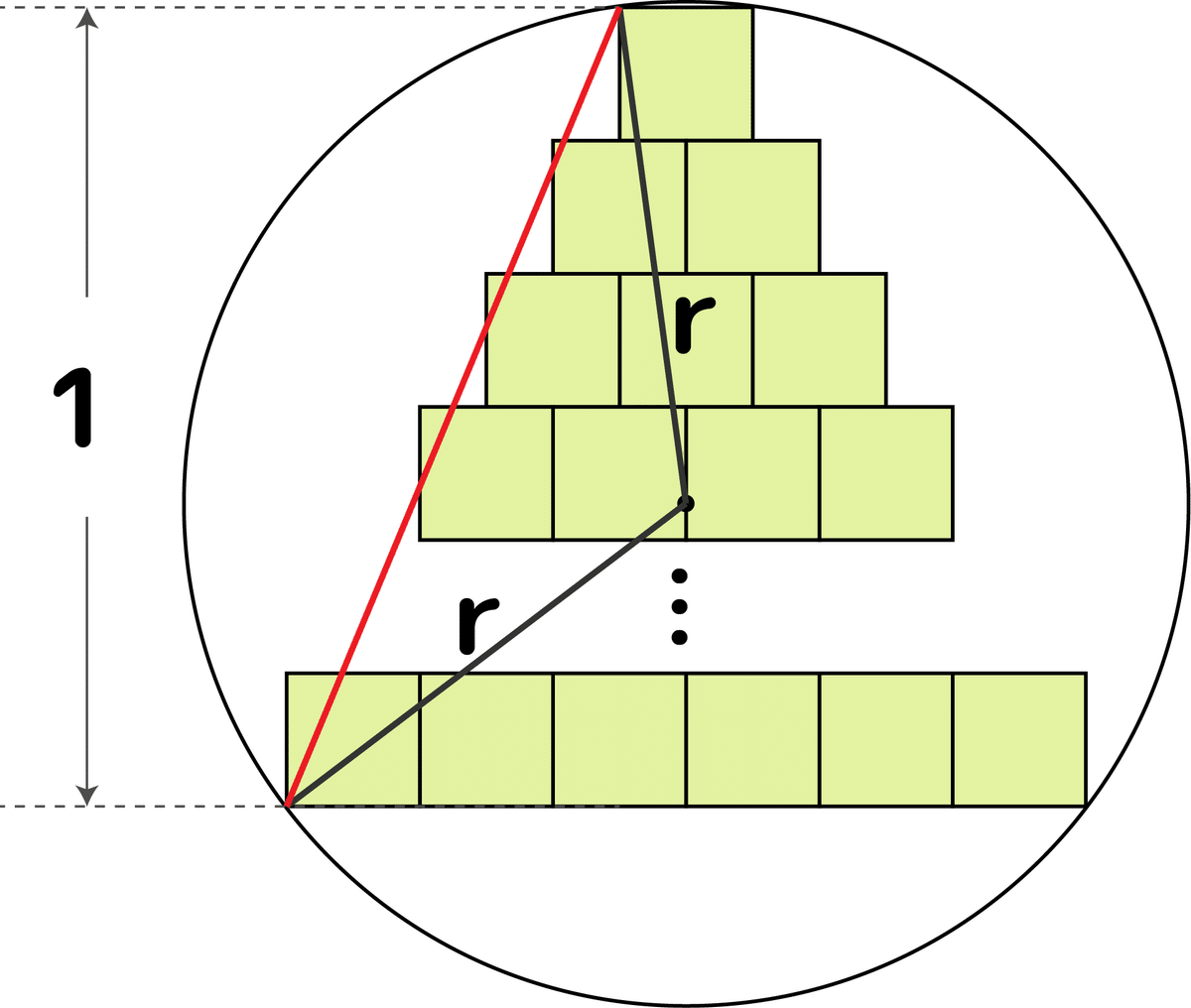
弦と中心点とには非常に嬉しい関係があります。弦の中点と円の中心点を結ぶ線分は弦と直角に交わります。つまり下図のように中点Bから弦に垂直な線を引くと中心点Oと交わります:

上図の三角形ABOは直角三角形になるので、ABとBOの長さがわかれば半径rもわかります。
弦の長さを求めよう
まずは弦の長さを求めてみます:

先のABは弦の半分の長さなので、弦ADの長さが分かればABの長さもわかります。直接求めるのは難しいので直角三角形の力を借りましょう。弦の端点である点Aからピラミッドの底辺まで垂線を引き、その足をCとします。ACはピラミッドの高さなのでAC=1です。
DCの長さはピラミッドの段数に依存しますが法則は単純です。ピラミッドの底面には段数nと同じだけ正方形が並びます。正方形に一辺は1/nなので、底面も長さは段数nによらず常に1になります。上図の点Cは底辺のど真ん中(点Cの右にあるライン)から正方形半分だけ左の位置にあるため、

と算出できるのがわかります。
ここから弦の長さADは、ピタゴラスの定理から、

このように表現できます。そして目的のABの長さはADの半分なので、

このように段数nから求める事ができます。一つ必要な長さが判明しました。後は直角三角形のもう一つの長さBOです。
相似を使ってBOを求めよう

BOは弦以上に曖昧な感じを受けます。Oは中心点でそもそも高さがわからないですし、Bも弦の中点ではありますが、それ以上の性質があるのか不明です。どうやらBOを直接求める事は難しそうです。
そこでBOを一辺に持つ直角三角形を作れないか考えます:

弦の中点Bからピラミッドの底面と平行な水平線を引きます。ピラミッドの中心線とその水平線との交点をEとします。すると真ん中の赤い直角三角形BEOができます。
次に青い直角三角形ACDに注目して下さい。この三角形は弦を求める時に注目した三角形で、辺の長さがすでに全部分かっています。そこから3辺の比も明らかです。
この直角三角形ACDと赤い直角三角形BEOは「相似」です。証明は簡単で、今∠ABOが90°で∠EBOは90°-∠ABE。この90°-∠ABEは∠BAEを求める式にもなっています。ここから∠EBO=∠BAEなので双方の直角三角形は相似となります(直角以外の一つの角度が同じなら2つの直角三角形は相似)。
という事で、赤い直角三角形BEOの辺のどれかがわかれば比率でBOの長さが求まります。候補はBEとEOですが、EOは中心点の位置が不明なので難しいです。消去法でBEの長さを求める事になります:

計算に必要な部分だけピックアップしました。BEとACの交点をFとします。こうすると点BはADの中点でBFとDCは平行なので、BFはDCの長さの半分になるのがわかります。そしてFEの長さは図から分かるように正方形の辺の半分です。正方形の辺の長さは1/nなので、結局BEは、

と段数nで表現できます。後は直角三角形の比から、

とBOの長さが求まりました。これで半径rがわかります!
半径rを求めよう

大詰めです。今ABもBOも段数nの式で表現出来ました。再掲しましょう:

後はピタゴラスの定理で半径rを求めるだけです:

途中計算はちょっと大変ですが、最終的には最下段がn段での外接円の半径となります。勿論解説1で導いた式と同じです。
深掘:nが無限大に飛ぶとどうなる?
ピラミッドの段数がどんどん増えて行くと、外接円の半径rはどうなるでしょうか?これは導いたrの式で段数nの極限を取ればわかりますね:

なんと有理数の5/8になります。
これの意味を紐解いてみます。ピラミッドを構成する正方形が限りなく小さくなっていった場合、ピラミッドは底辺が1、高さも1の二等辺三角形に漸近します:

上図の赤い直角三角形は斜辺が円の半径r、底辺が1/2、そして高さが1-rになっています。よってピタゴラスの定理から半径rを求められます:

極限で求めた5/8がちゃんと出てきました。
終わりに
ある図形を円や球などシンプルな図形で包むというのはゲーム制作で実は沢山出てきます。そういう図形を境界図形(Boundary Shape)と言います。キャラクタとか敵、地面など世界にある様々な物(オブジェクト)を境界図形で包みます。オブジェクトを境界図形で包む理由は、オブジェクト同士の衝突判定の計算負荷が軽くなる為です。キャラクタが地面に立つ時、実はキャラクタ自身ではなく境界図形が立っているんです。その境界図形はデザイナーさんが丁寧に手付でキャラクタに境界図形をフィットしてくれています。プログラマはキャラクタの動きに合わせてその境界図形も一緒に動かし、毎フレーム衝突判定を行っています。これによりゲーム内で衝突が生まれ、そこからイベントが生じ、それが積み重なってゲームが成立しているんです。今回の問題のような「包む」というのは、デジタルの世界では実は結構重要なんです。
ではまた(^-^)/
