
社会人のための学び直し数学【高校数学文字式編その1】
1.多項式の計算
$${5a^2b+3ab-a^2b+2ab}$$ の計算を考えてみます。
この式の構成要素は $${5a^2b}$$,$${+3ab}$$,$${-a^2b}$$,$${+2ab}$$ で,これらをこの式の項といいます。この式の項は 2 種類あって,文字の部分が $${a^2b}$$ となっているものと $${ab}$$ となっているものです。1 つの式の中で,文字の部分が同じ項を同類項といい,「$${5a^2b+3ab−a^2b+2ab}$$ を計算せよ」とは「$${5a^2b+3ab−a^2b+2ab}$$ の同類項をまとめよ」ということと同じです。
同類項をまとめるときは,文字の前の数字を計算(加法,減法による)して,文字をそのまま計算済みの数字の後ろにおきます。したがって,

となります。同類項をまとめたなら計算は終了です。ところで,最初の等号では交換法則を使って,同類項が計算しやすいように項を並べ替えています。このように演算(計算)の順序を入れ替えてもその結果が変わらないとき,その演算には交換法則が成り立つといいます。
【注】$${5a^2b}$$ は $${5×a×a×b}$$ のことで,これを一つのまとまり
(項)と考えることが大切です。
$${+3ab}$$,$${-a^2b}$$,$${+2ab}$$ も同様に数と文字のかけ算で,
それぞれ一つのまとまり(項)となっています。また,いくつかの項を
たし合わせた(1 個だけの場合もあります。)式を多項式といいます。
次に $${A=4x^2-3x+5}$$,$${B=-3x^2+4}$$ であるとして
$${5A-3(A-B)}$$ を計算してみましょう。
いきなり $${A}$$ や $${B}$$ に与えられた式を当てはめる(代入する)のは賢明ではありません。$${5A-3(A-B)}$$ を見てみると,$${A}$$ が 2 か所にあるので,これらをまとめることが最初にすべきことになります。
このとき,式の中に ( ) があるので,まず ( ) を外すことを考えます。( ) を外すときは分配法則を使います。分配法則は
$${a(b+c)=(b+c)a=ab+ac}$$
とできることをいいます。すると $${-3(A-B)=-3A+3B}$$ となります。符号の変化に注意してください。
よって,$${5A-3(A-B)=5A-3A+3B=2A+3B}$$ です。
この $${A}$$,$${B}$$ に $${A=4x^2-3x+5}$$,$${B=-3x^2+4}$$ を当てはめる(代入する)と

となります。2 番目の等号で $${8x^2}$$ と $${-9x^2}$$,10 と 12 はそれぞれ同類項です。また,文字を含まない 10 や 12 を定数項といいます。
【注】式を ( ) でかこって代入していることに着目してください。
練習問題 $${A=2x^2-5x-6}$$,$${B=x^2-4x-5}$$ のとき
$${5A-9B-3(A-2B)}$$ を計算せよ。
【答】$${x^2+2x+3}$$
【解説】$${5A-9B-3(A-2B)=5A-9B-3A+6B=2A-3B}$$
となるので,
$${2(2x^2-5x-6)-3(x^2-4x-5)}$$
=$${4x^2-10x-12-3x^2+12x+15}$$
=$${x^2+2x+3}$$
となる。
2.多項式の乗法
$${3a^2b×5ab^2}$$ の計算を考えてみましょう。
文字の乗法(かけ算)では次の指数法則を使います。
指数法則 $${a^m×a^n=a^{m+n}}$$
$${(a^m)^n=a^{mn}}$$
$${(ab)^n=a^nb^n}$$
数字は数字で,文字は文字でかけ算をします。
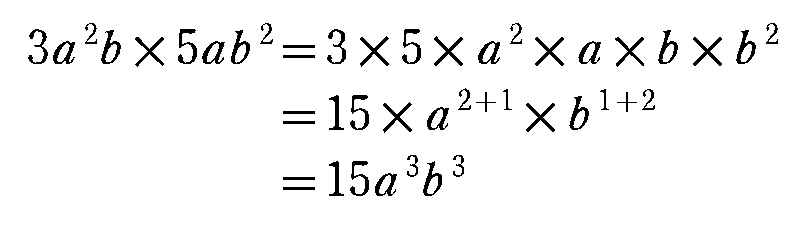
この計算の最初の等号では,積の交換法則を使ってかけ算の順序を入れ替えています。乗法には交換法則が成り立つのです。(積は「乗法したもの」という意味です。)
次に $${(x^2+5-4)(x^2-3)}$$ の計算を考えてみます。
いくつか準備をします。
1 つの項で,文字をかけ合わせる個数をその項の次数といいます。例えば
$${2a^2b}$$ は $${a^2b}$$ という文字の部分で,$${a×a×b}$$ と文字を 3 つかけ合わせているので次数は 3 です。さて,多項式を考えるとき,その項を次数の順番に並び替える(加法には交換法則が成り立ちます)と見通しがよく,計算がやりやすくなります。例えば $${x^2+5-4x}$$ は項ごとに次数を考えると 2,0,1 となるので,これを次数の高い(大きい)順(降べきの順といいます)に並べ替えると $${x^2-4x+5}$$ です。
【注】数の次数は 0 と考えます。
多項式の乗法では分配法則を使いますが $${(x^2-4x+5)(x^2-3)}$$ のままでは考えにくいので $${x^2-4x+5=A}$$ とおいてみましょう。すると
$${A(x^2-3)=Ax^2-3A}$$
となり,この後 $${A→x^2-4x+5}$$ と,もとに戻します。そして,
$${(x^2-4x+5)x^2-3(x^2-4x+5)}$$
=$${x^2×x^2-4x×x^2+5×x^2-3×x^2+3×4x-3×5}$$
となります。これは $${(x^2-4x+5)(x^2-3)}$$ で後ろの式の各項
$${x^2}$$,-3 を前の式の各項 $${x^2}$$,$${-4x}$$,+5 のそれぞれにかけた形になっています。そこで,この計算には次のように分配法則を使うと考えます。

また,前の式の各項 $${x^2}$$,$${-4x}$$,+5 を後ろの式の各項 $${x^2}$$,-3 のそれぞれにかける分配法則の使い方もあります。

いくつかの多項式の積の形を計算して,1 つの多項式にすることを式を展開するといいます。
練習問題 次の式を展開せよ。
(1)$${3abc(a-2b+3c)}$$ (2)$${(3a-2b)(a^2-4ab-b^2)}$$
(3)$${(3x-2+x^2)(2x^2-x-3)}$$
【答】(1)$${3a^2bc-6ab^2c+9abc^2}$$(2)$${3a^3-14a^2b+5ab^2+2b^3}$$
(3)$${2x^4+5x^3-10x^2-7x+6}$$
【解説】(3)前の多項式を降べきの順に並び換えた
$${(x^2+3x-2)(2x^2-x-3)}$$を計算する。
いいなと思ったら応援しよう!

