
Python勉強記(6)- 関数
初めに
高等学校では「情報Ⅰ」という科目が何年も前から教えられており、大学センター共通テストでも出題されています。大学入試センター共通テストの「情報Ⅰ」では、DNCLと呼ばれる共通テスト専用のプログラミング言語が使用されるようです。
第二の記事にはコードの例が記載されています。Pythonを強引に日本語化し(+不可解なブロック表記)、プログラミングの配点が最も高いとのことです。
特定の言語に依存しない問題であれば理解できますが、少なくとも、コンピューターで入力可能な言語であるべきです(私感)
話が逸れましたが、始めます。
Python の関数
Pythonでは、他のプログラミング言語と同様に、様々な関数を利用したり定義したりすることができます。
関数はPythonのコード内で値を受け取り、プログラムを実行し、そしてユーザーが求める値を返します(引数や値は必ずしも必要ではありません)。これはC言語や他の高級言語と同様です。
関数を変数と区別するために、名前の後に()を付け、func()のように表します。これは以前からの慣習です。
分類
関数は主に、実装方法によっていくつかのカテゴリに分けられます。
分類方法は様々ですが、簡単な検索で見つけた以下の記事の分類が、説明したい内容に近いので、これを使用することにしました。
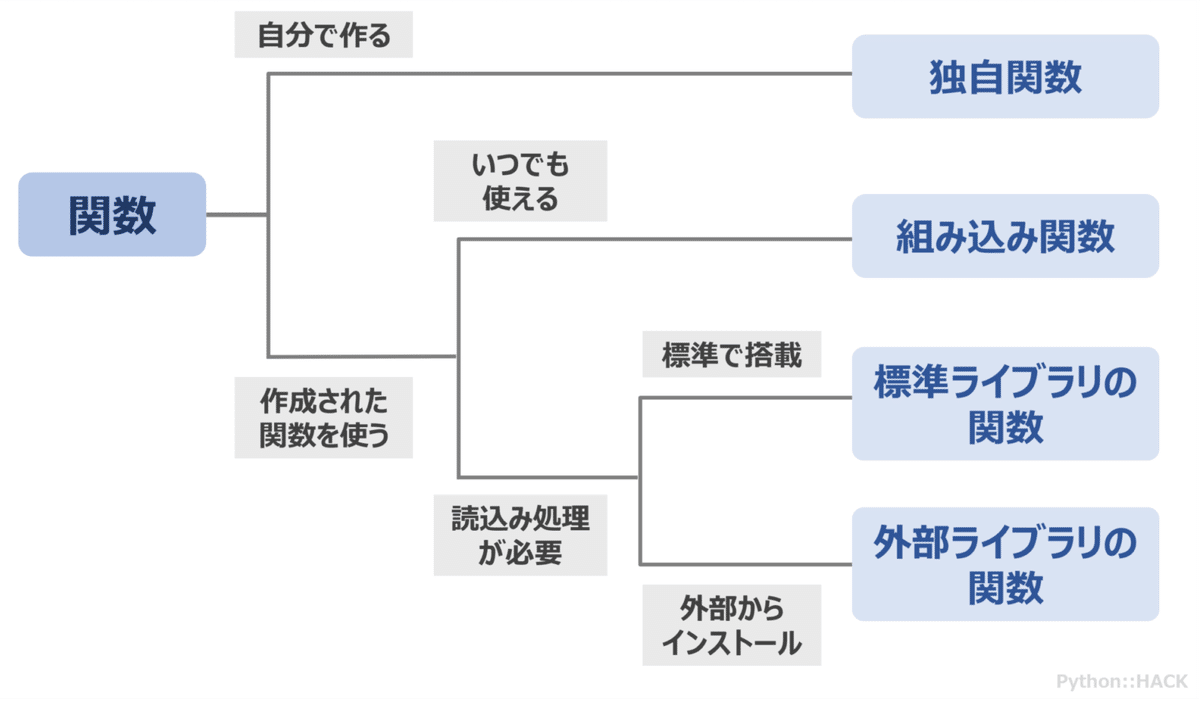
うん。とってもわかりやすい。
続き要らなくね?
・・・
解説書ならその通りですが、これは勉強記ですので
自分なりにかみ砕いたテキストを書き続けます。
組み込み関数
上記の「関数の分類」図における2番目のカテゴリーは、Pythonに組み込まれており、すぐに使用可能な関数群です。
これまで何度も使用されてきたprint()や入力関数のinput()、算術関数の中で絶対値を返すabs()などが、組み込み関数に該当します。
組み込み関数一覧(公式ドキュメント)
【一部修正】標準ライブラリの関数
組み込み関数でない関数は、import文を使用して読み込む必要があり、通常はライブラリ名.関数名()の形式で呼び出します。これらの中で、Pythonインストーラに最初から含まれており、import文だけで使用できる関数を「標準ライブラリ関数」と呼びます。
典型的なライブラリは数学ライブラリmath です。
math --- 数学関数 — Python 3.12.4 ドキュメント
以下に、π/4(45度)の正弦、余弦、正接の値を示します。
>>> import math
>>> print(math.sin(math.pi/4)) # surt(2)/2
0.7071067811865476
>>> print(math.cos(math.pi/4)) # sqrt(2)/2
0.7071067811865476
print(path.con(PI/4)) # 1
0.9999999999999999
円周率を表すには`math.pi`と記述する必要がありますが、これを面倒だと感じる方々(私も含めて)のために、2種類の構文が用意されています。
1.import ライブラリ名 as 別名
>>> import math as mt #ライブラリに別の短い名前を付ける。
>>> mt.sin(mt.pi/4.0)
0.70710678118654762.from ライブラリ名 import 関数1, 関数2…
>>> from math import pi, sin, con, tan # 関数を指定してライブラリ名を省略する。
>>> sin(pi/4.0)
0.7071067811865476可読性の観点からは、最終的な方法が最もすっきりしていて良いと思われますが、やり過ぎは以下のような問題を引き起こす可能性があるため、注意が必要です。
名前の衝突
プログラムの移植性が損なわれる
本来使用可能な関数が使えなくなる
例えば、from math import ~を使用する場合、利用する関数を全て明記する必要があります。この場合、asin()関数も呼び出せると誤解する可能性があります。
>>> from math import pi,sin,cos,tan
>>> sin(pi/4)
0.7071067811865476
>>> asin(0.7071067811865476) # arcsin((sin(pi/4))を計算してみる。
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'asin' is not defined. Did you mean: 'sin'?
>>> math.asin(0.7071067811865476)
0.7853981633974484以下はライブラリ名を知らなければ困難な例です。何が誤っているのでしょうか?
1行目で取り込んだはずのexp()は$${e^x}$$ですが、実数値関数であるため、オイラーの公式を計算することができません。
この場合、複素数用のライブラリであるcmathを使用する必要がありました。
>>> from math import pi, e, exp ♯オイラーの公式でe^(iπ)を計算する
>>> e**(1j*pi)
(-1+1.2246467991473532e-16j) # OK(丸め誤差あり)
>>> exp(1j*pi) # math.exp() は実数のみ計算できる。
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: must be real number, not complex
>>> import cmath # 複素数用ライブラリを慌ててインポート
>>> cmath.exp(1j*pi)
(-1+1.2246467991473532e-16j)【追記あり】外部ライブラリの関数
Pythonのインストールには含まれていないが、別途インストールが必要なライブラリがあります。その中でも、高度な数学ライブラリであるNumPyは特に有名です。
>>> import NumPy #そういえばNumPyインストールしていなかった。
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ModuleNotFoundError: No module named 'NumPy'★公式Pythonでは、pip コマンドを使用してインストールしたら使用できるようになるはずですが、当方の環境でエラーになり調査中です。
調べてみたところ、ライブラリのパス設定が必要でした。
【付記】Numpyのような外部ライブラリを複数インストールする際には、公式Pythonのpipコマンドでは依存関係が解決しないことがあります。そのような場合、Anacondaに付属するcondaコマンドが必要になることがあります。詳細は後ほど記事にてご紹介します。
独自関数
標準ライブラリに必要な関数がない場合や、独自の関数を作成したいときがあります。
これから様々な関数やプログラムを作成していく予定ですが、今は概要だけに留めておきます。
公式ドキュメントにもあるフィボナッチ数列のプログラム例を紹介します。
フィボナッチ数列は、以下の漸化式で定義される数列です。
$$
a_0 = 0, a_1=1 \\
a_{n+2} = a_{n+1} + a_{n} ( n > 2)
$$
Pythonプログラムでは以下のようになります。
※プロンプト記号は省略しました。
# Python 3: Fibonacci series up to n
def fib(n):
a, b = 0, 1
while a < n:
print(a, end=' ')
a, b = b, a + b
print()
fib(1000)
独自関数の構造はおおよそこのようなものです。
def 関数名( 引数1, …):
いろいろな処理
[ return 値 ]
# ここからがメイン処理
なにかの処理
[ 変数 = ] 関数名( 引数1, …)
Pythonプログラミングの理解が進んできたところで、今日は要点を確認し、次回に持ち越します。
関数は使用する前に定義する必要があります(変数も同様です)。
関数定義の後に実際の処理文を記述します(defと書いただけでは実行されません)。
ブロックはインデントを使ってオフサイドルールに従って記述します。
