見出し画像

ロディンフラクタル−前編−

marten345marten

前書き

　今回の記事はロディンフラクタルについて。知ってはいるけれど何なのかよく分からないという方、そもそもロディンフラクタルとは何なのさ？という方へ向けた記事になります。前編・後編ともに難しい数式は出てきませんので、是非最後まで読んでいって下さい。

と、本題に入る前に。

　ここ最近、Twitterもnoteもフォロワーさんが増えていて驚いています。
それに伴い心境にも変化がありましたので、本題のロディンフラクタルに入る前に少しだけ綴らせて下さい。

　Twitterはつぶやきなので今のままでも良いのかもしれませんが、noteは今のままでは失礼なのでは？と思いました。

　と言うのも、Twitterの延長線でnoteを使っており、好き勝手気分で記事を書いていました。ですが、せっかく私に興味を持ってフォローして下さっている方がいるのに、このままの姿勢では申し訳ないと思いました。

　そこで今後のnoteではビギナーさん向けの記事や、解説記事にシフトしていこうと思います。

　実は私は、霜月やよいさんに勉強を見てもらっている身でして、霜月さんとフォロワーさんに恩返しとなる様な記事を書いていこうと思い立ちました。（私もアウトプットになって良いですし！）

　霜月やよいさんの情報発信や、理の知恵の凄さ・深淵さはわかるけれど理解しきれていない方、この手の知識を学び始めたばかりのビギナーさんに向けて、拙い文章ながら記事を綴っていこうと思います。なるべくライト目な記事を心がけていきますので、どうぞ気軽に読んでやってください。
※私も学んでいる身ですので、違う視点やご意見・リクエストなどあれば是非TwitterにてDMください。励みになりますので！


暑苦しくなっちゃいました。そろそろ本題に入りましょう。



ロディンフラクタルとは？

　そもそもロディンフラクタルとは？という方のために簡単に解説しておきます。ロディンフラクタルとは、マルコ・ロディンという人物が提唱した数の考え方で、０〜９、１０種類の数を九角形の幾何学に落とし込んだものです。

　この幾何学からこの世の根本原理・数の性質が読み取れます。何とも仰々しい感じがしますが、賢者の言葉を思い出してみましょう。

「宇宙は数学という言語で書かれています」
「幾何学は永遠に存在するものについての知識です」
「万物の根源は数」

ガリレオ・ガリレイ、ピタゴラス、ピタゴラスの順


※ここで注意して頂きたいのが、生命の樹やテトラクテュスなども１０の数で表したりします。ですが今回はロディンフラクタルについて。
　表し方が違うだけでどちらも根本原理についてのものなんですが、一緒に考えるとややこしくなります。ですので今回は分けて考えていきます。


　ではロディンフラクタルを通して「この世の根本原理・数の性質」を見ていきましょう。



０

数の概念

　本題に入る前に”数”について少しだけ。我々が日頃使用している十進法では、0.1.2.3.4.5.6.7.8.9と数字を１ずつ足していき、位が増えても10.11.12.13…という具合で数は増えていきますね。
　これは０〜９の１０種類の数字という文字の並びで数（かず）を表しています。

　この１０種類の数字から「この世の根本原理・数の性質」が読み取れるのですが、ひと工夫してそれを表したものがロディンフラクタル。
　では各数字をロディンフラクタルに落とし込んでいきます。



始まりであり最大の「０＝円」

　はじめに０から。０はロディンフラクタル上の数字には記されていませんが存在しています。そう、見えないけれど存在している。

　勿体ぶらずに言いますと０は円です。いきなり素っ頓狂なことを言っているわけではありませんよ。

０＝円


　０という形が円だからってのも理由なんですが、この記事ではちょっとだけインテリっぽくいきましょう。
　円は立派な根本原理。作図において、一番最初に描くのは円。円（０）は全ての始まりであり、最大のものです。

多角形の作図

　だから０は外周の円で表します。いまいちピンと来ませんか？抽象的に感じるかもしれませんが、これでも具体的に述べているんです。上記太字の一文をインプットして頂いて次を見ていきましょう。


繰り返しの１２４８７５


掛け算

　次に１２４５７８。３６９は前回の記事で触れただけですが、特別な数字というイメージは掴めていると思います。（まだの方はリンクをどうぞ）
　なので今回は前回の記事では登場していない残りの数を紹介します。


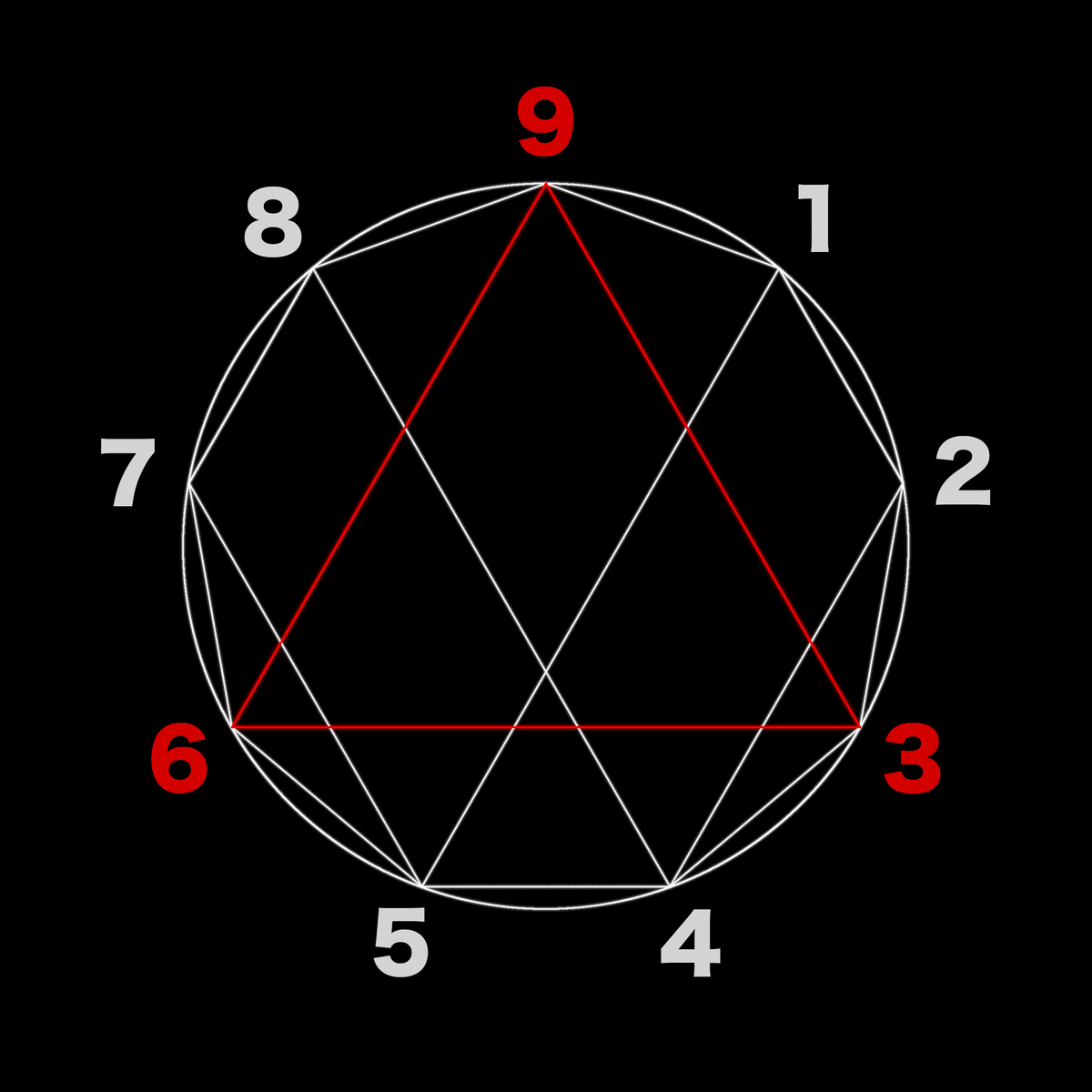
　ロディンフラクタルに目を向けると３６９と１２４５７８は別々のグループになっており、１２４５７８を矢印が辿っています。

　ですが、見ての通り１２４５７８の順番ではなく、１２４８７５の順番で辿っています。

　５と８を入れ替えただけですが、この並びでないといけないんです。
先ほど登場した「一番最初に描くのは円。円（０）は全ての始まりであり、最大のものです」の一文がここで繋がります。

　では数字を並び替えた理由と、０＝円である理由とを説明していきましょう。深淵さを炙り出すにはめっちゃ簡単な数式が必要なだけ。それは掛け算。倍々（×２）にしていきます。

1.2.4.8.16.32.64.128.256.512.1024.2048.4096…

　次に倍々にしていったをそれぞれ一桁にします。16ですと１＋６＝７という具合。（カバラ式）
そうすると…

1.2.4.8.7.5.1.2.4.8.7.5.1…

　１２４８７５が顔を出しました。この倍々（×２）とカバラ式の手順から得られた１２４８７５は、順番はそのままに同じ数字の並びが無限に繰り返します。そして３６９は登場していません。

　これがロディンフラクタルにおいて３６９と１２４５７８が別のグループである理由であり、辿る順番が１２４５７８ではなく１２４８７５である理由です。


　ですがこの世の理は似て非なる対。拮抗が原則。磁石のS極・N極、男女、太陽と月、左右…と例をあげれば枚挙にいとまがありません。

「似て非なる対」の例として太極図。陰と陽。

　まだプラス方向（掛け算）だけしか説明していませんので、今度は対になるマイナス方向（割り算）も見ていきましょう。掛け算だけでは結びつかなかった０＝円もここで結びつきます。


割り算

　割り算は以下の手順で。先程「円（０）は全ての始まりであり、最大のものです」と書きましたが、これを割り算します。と言っても０を割っても０になるだけですので、360で割ります。

　360の理由は、円の角度は360度だから。円よりも大きい角度は存在せず最大の角度である360を割り算していきます。では実際に割り算していきましょう。

360÷1=360
360÷2=180
360÷3=120
360÷4=90
360÷5=72
360÷6=60
360÷7=51.42857142857145…
360÷8=45
360÷9=40

　360度（円）をそれぞれ割り算しました。概ね割り切れるのですが７だけが割り切れていませんね。そして見ての通り順番こそは異なりますが１２４８７５と同じ数字が炙り出せました。

　ここで注目して頂きたいのがまたしても数字が繰り返すということ。360÷7は割り切れないので小数点以下の数字は無限に続くのですが、割り算からも同じ数字の繰り返しが見出せました。しかも割り算でも３６９を除いた１２４５７８ですね。


小まとめ

　と、途中で抽象的な表現も含みましたので、一旦ここまで説明してきたことのポイントをまとめて前編は終わりにしましょう。


ここまでロディンフラクタルとは何ぞや？からはじまり、

  • ０＝円(360)

  • ３６９と１２４５７８は別のグループ

  • １２４８７５の順番で巡る

  • 円を割り算しても、数字を掛け算していっても３６９を除いた１２４８７５が現れた

  • 現れた数字は繰り返しだった

　ということを説明してきました。ここまで具体例を何も挙げていなかったので「１２４８７５」についての知恵をひとつだけ。
　細胞分裂・音符記号・ホルスの目も一桁にするカバラ式を適用すると同じ数字が見出せます。（↓ツイート参照）



　本当は一本の記事にしたいのですが、文字数的にライト目な記事になりませんので前編はここまでにします。後編では続きの「３６９」の説明と、ロディンフラクタルから見えてくる「この世の根本原理・数の性質」を紹介したいと思います。




おまけ

　まだ消化不良な方のためにおまけで。ロディンフラクタルの解説からは脱線するので混合しないようにして下さいね。混合しそうでしたらスルーして下さい。


「０＝円と±」

　陰(−)と陽(＋)と０＝円。作図で一番最初に描くのは円。円（０）は全ての始まりであり、最大（360）のもの。０＝円の中に陰と陽が存在しています。また、太極図には黄金比。表し方が違うだけで根本原理について表したもの。

「あらゆるものは、他のあらゆるものと関連する」

レオナルド・ダ・ヴィンチ





　今回の記事と上記とを読んだ後に霜月やよいさんの著書『As above so below』の「Number０.１」「Number２」を読んでみて下さい。以前よりはわかるようになっているはずです！抽象的に書かれているようで具体的に書かれている不思議な本だと私は思っています。

　注意を重ねますが、今回の記事はロディンフラクタルについて。表し方が異なりますがそれぞれは同じ様に根本原理を表したもの。

　ちなみに次の後編は「Number３」とリンクする内容です。後編もお楽しみに！




秘密はいつも目の前に。


※無断での引用・転載禁止※
本記事を引用・転載されたい方はTwitterにてメールして頂けましたら対応します。
noteプロフィールにあります、Twitterアイコンからどうぞ。