
黄金比の世界-無限の世界のフラクタル-
本日の記事は「黄金比」について。
以前Twitterにて「黄金比」をスレッドとしてまとめていました。
現在はまとめの場がnoteに移ったので、それに当たってnote版の記事を書こうと思い、今回の記事です。
Twitterの1ツイート(140文字)とは違い、文字制限もないのでまとめやすいですし。
「黄金比」は私が様々なことに興味を持つキッカケでもあり、原点回帰を込めての記事になります。
シンプルなことですので数学苦手でも大丈夫!
それでは早速いってみましょうー!
黄金比とは
では早速ですが「黄金比」をご存知でしょうか?
絵画や建築物、デザインなどを通して黄金比をご存知の方もいらっしゃるのではないでしょうか。
では黄金比とは?と聞かれたらちょっと言葉に詰まってしまいません?
プラトンは著書『国家』の中でついて次のような言葉を残しました。
(プラトン登場ですが苦手意識を抱かないで下さいね!)
「1本の線分をとり、それを等しからざる部分に二分せよ」
プラトンは「黄金比」のこととは言及していませんが、上記は「黄金比」のそれです。

ですがプラトンの遺した言葉だけではサッパリ分かりませんよねw
この記事を通して「黄金比」を身近に感じていただきたいので、
「そもそも黄金比とは何ぞや?」についてザックリ説明しますと、
黄金比とはこの世の”根本原理”です。
黄金比が根本原理と言われてもあまりピンと来ないですよね。
では少し噛み砕きますと、
我々人間や動物、植物、スケールを大きくして宇宙、自然界のモノは黄金比で構成されている。
特別な比、黄金比という律(ルール)に自然界は従っている。

と、言う具合でしょうか。
では早速その「黄金比」について見ていきましょう!
自然界を構成する特別な比、黄金比とはどのような比なのか?
それは「1:1.618…」という比です。(※1.618…は小数点以下が永遠に続く”割切れない”数字・無理数です。そのためΦ(ファイ)という記号で表記します)

なぜ特別かと言いますと、先のプラトンの言葉を思い出しましょう。
「1本の線分をとり、それを等しからざる部分に二分せよ」
このプラトンの言葉を理解するには”等しからざる部分”がポイントになります!
プラトンのあいまいな言葉を言い換えてみますと、
「(等しからざる部分で二分した)長い線分と全体の線分の比が、長い線分と短い線分の比と等しくなる」
そのような比が特別な比で、「1:1.618…」という比です。
言葉だけではイメージし難いですので、画像を交えながらプラトンの言葉を理解してみましょう!
まずはじめにプラトンの言葉と反して「1本の線分を”等しい”部分で二分したもの」を例にみてみます。
1本の線を”等しい”部分で二分したならその比は「1:1」となります。
そして全体の線分と二分した線分の比は「2:1」となります。
これではありふれた比で、プラトンがわざわざ言葉で遺すほどの比ではありませんね。
プラトンわざわざ言葉で遺したのは特別な比についてです。
ではプラトンの言葉通り「1本の線分を”等しくない”部分で二分したもの」をみてみましょう。
画像をご覧ください。
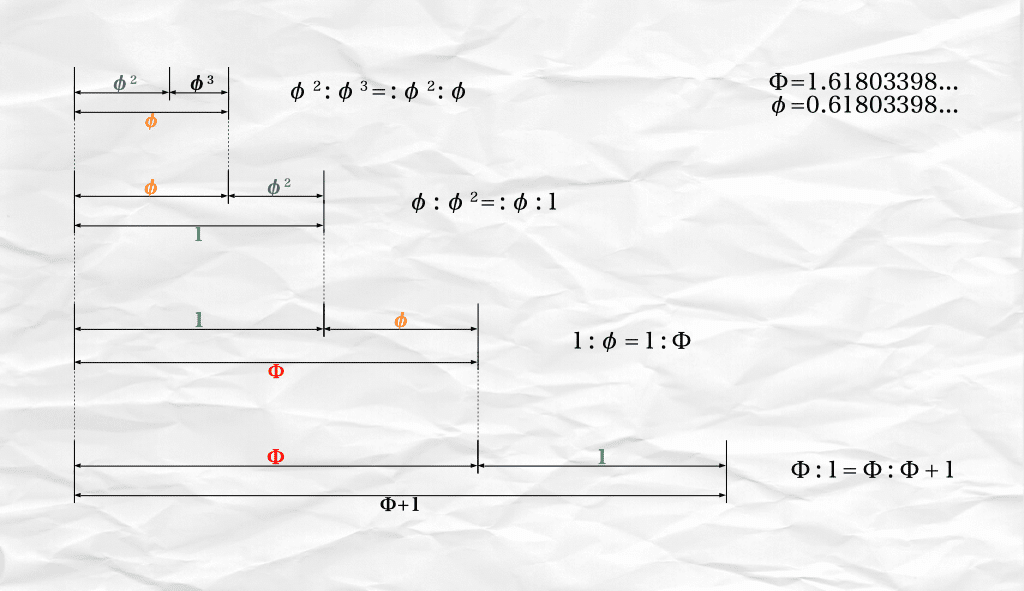
等しくない部分で二分した長い線分と全体の線分の比は「1:1.618…」です。
そして長い線分と短い線分の比も「1:1.618…」です。
そして更に短い線分とそのまた短い線分の比も「1:1.618…」と。
”等しくない”部分で二分された線分の比は無限に「1:1.618…」となる特別な比なのです!
だからこそ、プラトンはわざわざ言葉で遺したのです!
この特別な「1:1.618…」という比を黄金比と言います。
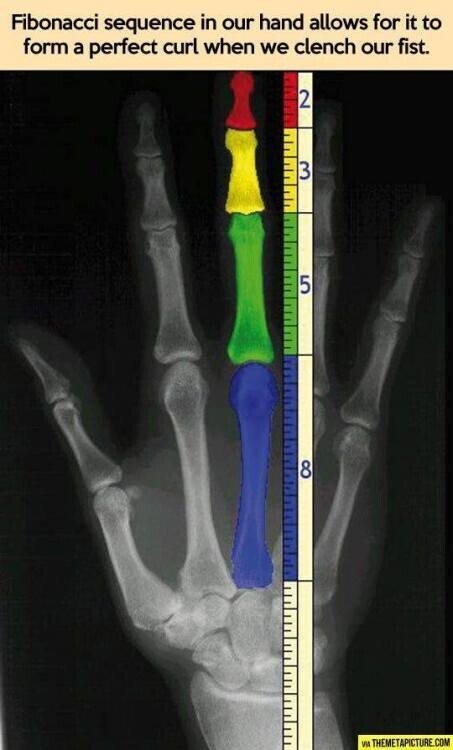
この特別な黄金比(1:1.618…)、「自然界を構成する比」と先述していましたので身近な例を一例を挙げますと、人間の手指の骨は黄金比になっています。
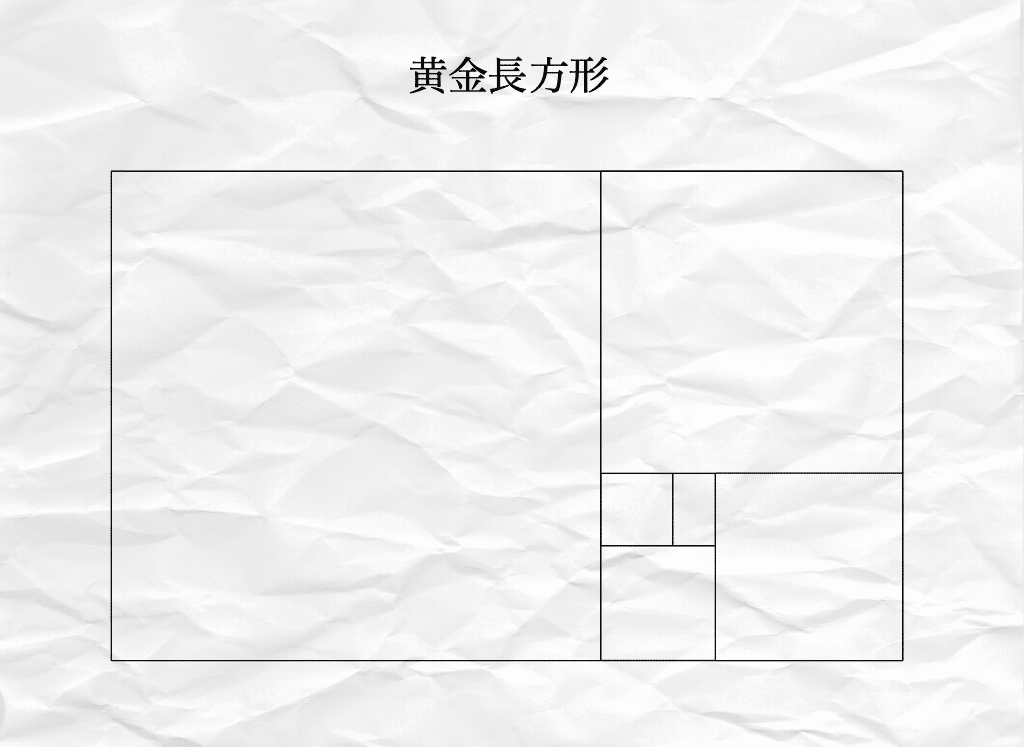
黄金長方形
では黄金比(1:1.618…)について説明しましたので、視点を変えてみましょう!
一次元(線の世界)から二次元(面の世界)へ!
以下の画像は「黄金長方形」と呼ばれるものです。
名前に”黄金”とついていますので、察しの通り黄金比(1:1.618…)で構成された長方形です。
黄金長方形の中に正方形を描きます。すると残りの部分も黄金長方形になります。
そしてまた黄金長方形の中に正方形を描くと、残りの部分はまた黄金長方形に…と無限に繰り返し描くことができます。
なぜ無限に黄金長方形を繰り返し描けるかというと、前項の「黄金比(1:1.618…)」は無限に分割できる特別な比でしたよね?
それが一次元(線の世界)から二次元(面の世界)へと移っただけだからです。

黄金長方形の例を挙げますと、自然界の物ではありませんが建築物や石板などにその智慧は遺されています。


黄金長方形も自然界に顕れるのですが、一つ手を加えた方が、誰もが見たことのある馴染みのある物になります。
もちろん、「黄金比(1:1.618…)」で構成された手指の骨のように、あなた自身にも顕れている物です。
一次元(線)から二次元(面)、そして我々の住む世界、三次元(立体)へ…
ではそのことを踏まえつつ次の項へ移りましょう!
黄金螺旋
では引き続き黄金長方形に登場してもらいます。
”一つだけ手を加える”、それは螺旋を描くことです。
黄金長方形の中に正方形を描くと、残りの部分はまた黄金長方形が顕れる…という無限の繰り返しを説明しました。
その黄金長方形の中に描いた正方形、その正方形の対角に弧(円の一部)を描いていきます。
すると、この弧も無限の繰り返しの螺旋になります!
この螺旋が「黄金螺旋」です。

他にも「黄金比(半円)の螺旋」や「黄金三角形の螺旋」などもあります。
もちろんすべて黄金比(1:1.618…)で構成されています。


前項「黄金長方形」で述べました”一つ手を加える”こと、つまり螺旋。
螺旋が顕れることによって「自然界の誰もが見たことのある馴染みのある物」になります。
では「黄金螺旋」が我々の住む三次元(立体)に顕れたものを見てみましょう。
銀河も黄金螺旋を描いています。

スケールを小さくして太陽系も黄金螺旋を描きながら銀河を回っています。

更にスケールを小さくして、台風も黄金螺旋。

更に更にスケールを小さくして、あなたが握ったその拳も黄金螺旋。
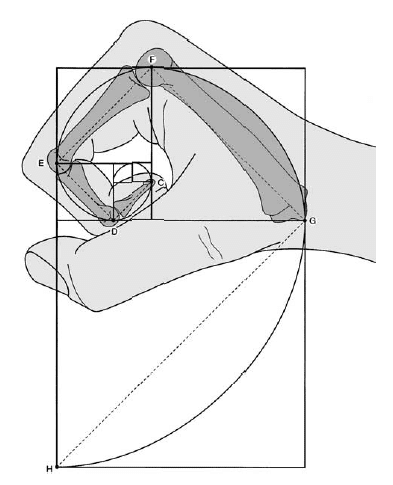
そして、音(音波)も黄金螺旋。

その黄金螺旋の音が届くのは耳(耳介)、耳も黄金螺旋。
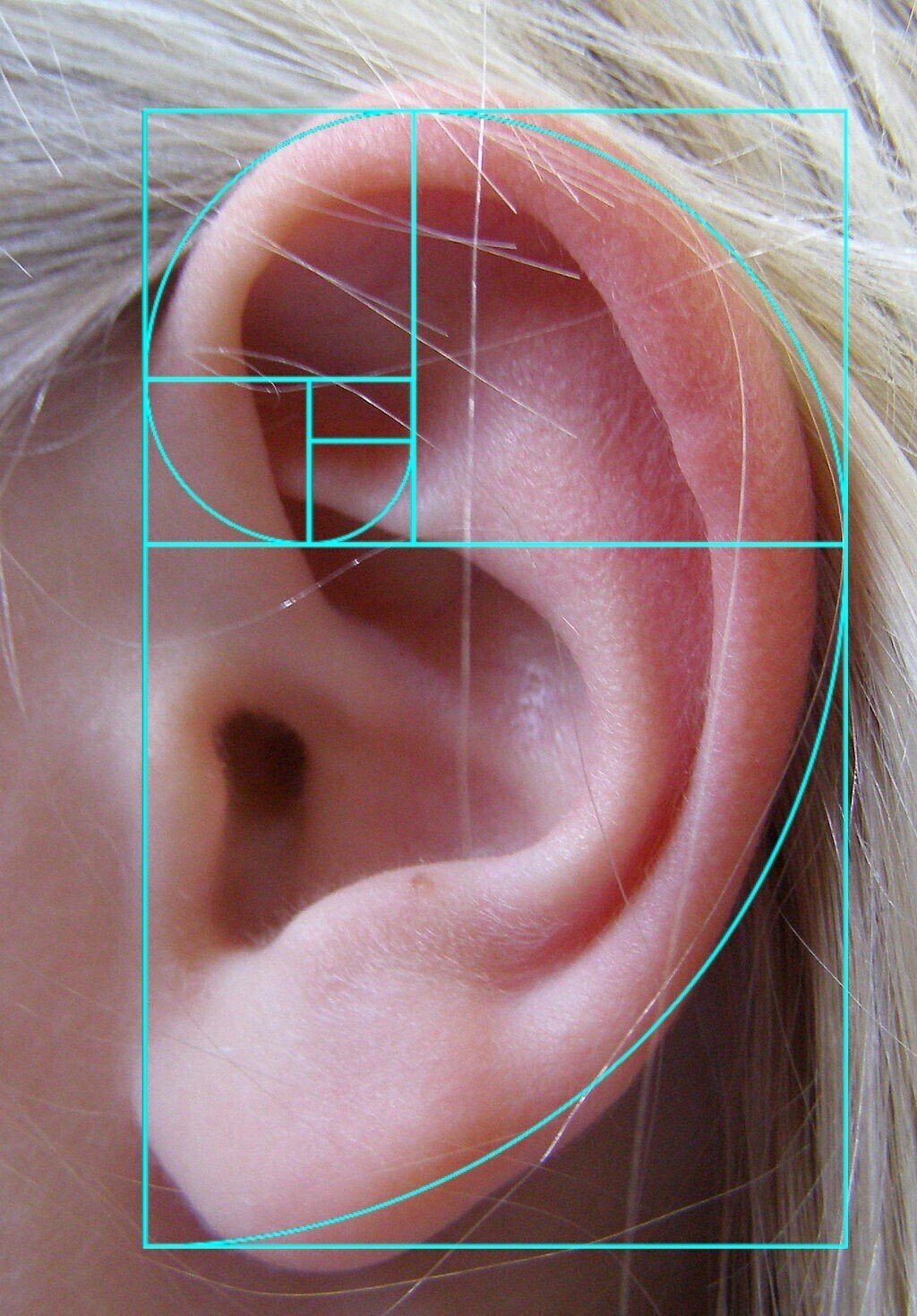
黄金螺旋の耳から鼓膜を介し、見ての通り黄金螺旋の蝸牛へと黄金螺旋の音は進み、そして脳へ…

この様に我々の住む自然界は、特別な比、黄金比という律(ルール)に従っています。スケールの大きいものも、小さいものも同じように黄金螺旋(黄金比)で構成されています。
そのことを古代の賢人たちは次の様な言葉で遺しました。
「As above so below(上の如く、下も然り)」

我々人間や動物、植物、スケールを大きくして宇宙、自然界のモノは黄金比で構成されています。
自然界は、特別な比、黄金比という律(ルール)に従っているのです。
★(五芒星)
自然界を構成する要素・根本原理である「黄金比(1:1.618…)」
古代の賢人たちは自然界を深く観察し、この智慧(ちえ)を発見しました。
もしあなたが古代の賢人であれば、この智慧を後世に遺そうとはしませんか?
プラトンが「1本の線分をとり、それを等しからざる部分に二分せよ」という言葉を遺したように。
プラトンは言葉で遺しましたが、別の賢人は幾何学で…分かる者に対し象徴として遺しました。
それが「★(五芒星)」です。

といっても5枚花弁の花を見れば、★(五芒星)が見てとれますが、黄金比との繋がりを理解するには智慧が必要です。

「理(ことわり)を解る」ための智慧が。
では早速その智慧を見てみましょう!
五角形に対角線を引くことによって「★(五芒星)」を描くことが出来ます。

この「★(五芒星)」は黄金比(1:1.618…)で構成されています。

ここで注目して頂きたいのですが「★(五芒星)」は前の項で軽く触れた「黄金三角形」で構成されています。
「黄金三角形」も黄金比(1:1.618…)で構成されていましたね!
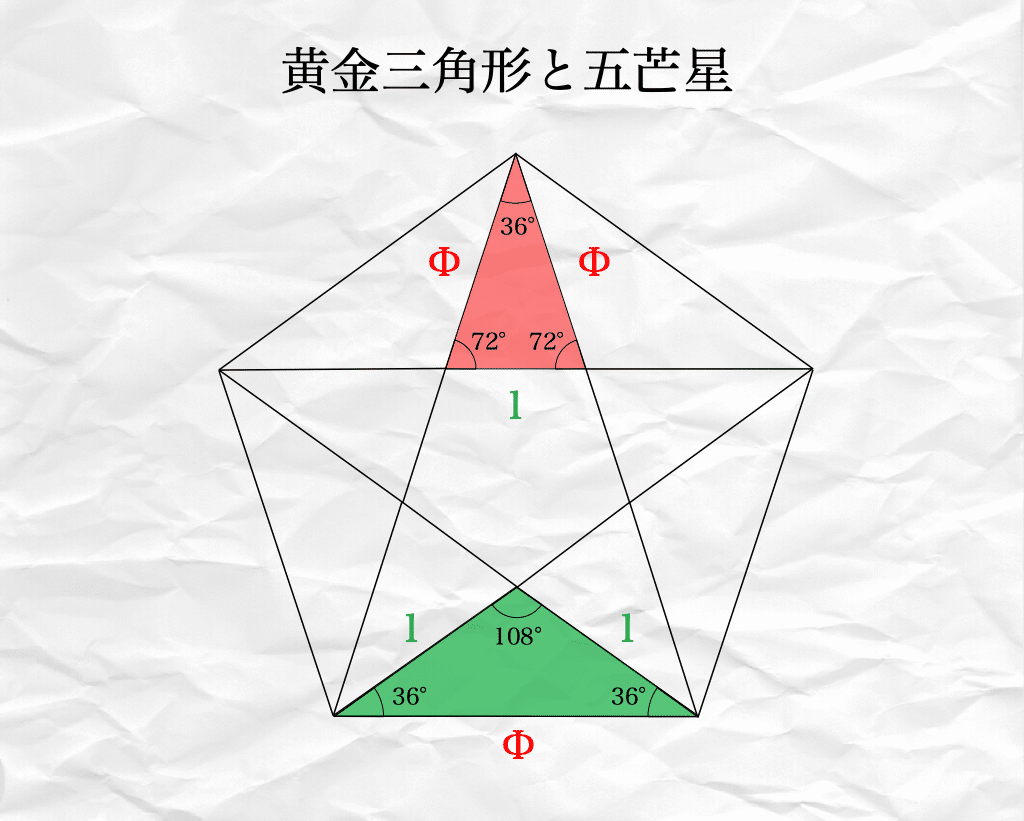

そして今までの項で見てきたように、「黄金比(1:1.618…)」で構成されているものは無限の繰り返しをしていました。
「★(五芒星)」も「黄金比(1:1.618…)」で構成されているので、無限の繰り返しを見出せます。
またしても「黄金三角形」に形作られながら…(自己相似)

ではこの項のまとめとして、先ほどの花へ「★(五芒星)」をトレースしてみます。
どうでしょう?やはり「黄金比(1:1.618…)」で構成されていますね!

今回の記事では触れませんが、五角形は三次元へ顕れる鍵となる図形です。
この説明も追々していきますので次回以降の記事をお楽しみに!
フィボナッチ数列
ではこの記事最後の項になります「フィボナッチ数列」について見ていきましょう!
数学が苦手でも大丈夫ですよー!
「フィボナッチ数列」は、ただただ足し算をしていくだけですので!
一般的に認識されている数字の増え方ですと、
1.2.3.4.5.6.7.8.9…
と1ずつ数字を足していくのが一般的です。
ですが、自然界においては異なります。
ここまで見てきたように、自然界は黄金比(1:1.618…)で構成されていましたよね?
ですので、自然界の数字の増え方も黄金比(1:1.618…)に則って増えていきます。
ではどの様に数字が増えていくのでしょう?
その数字の増え方は以下通り。
0.1.1.2.3.5.8.13.21.34.55.89.144.233.377.610…
数の増え方は、0と1から始まり、前2つの数字を足しながら増えていきます。
0+1=1
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21
という具合です。
この足し算の数列が「フィボナッチ数列」と呼ばれるものになります。
例外もあるのですが、自然界の数字の増え方は「フィボナッチ数列」のように増えていきます。
ですが「自然界を構成する黄金比(1:1.618…)」が見当たりませんよね?
黄金比(1:1.618…)を見出すには少し智慧が必要です。
その智慧とは割り算です。
上記の「フィボナッチ数列」の数字をそれぞれ割り算(つまり比)をし、その値を求めます。
それぞれの数字を割り算していくと、その値は徐々に極限値であるΦ(1.618…)へと近づいていきます!


自然界の数の増え方「フィボナッチ数列」からも「黄金比(1:1.618…)」が見出せましたね!
ですが、数字を眺めているだけでは自然界との繋がりは実感しづらいですので、この項でも例を挙げて見ましょう!
松ぼっくりの笠も螺旋を描いていますが、その螺旋の本数は時計回り8本、反時計回り13本。
フィボナッチ数列(0.1.1.2.3.5.8.13.21.34…)です。

また理想的な枝葉の分岐もフィボナッチ数列

雷や河川の分岐、鹿の角も同じですね。



そして血管の分岐も

脳のニューロンと宇宙も同じ仕組みです。
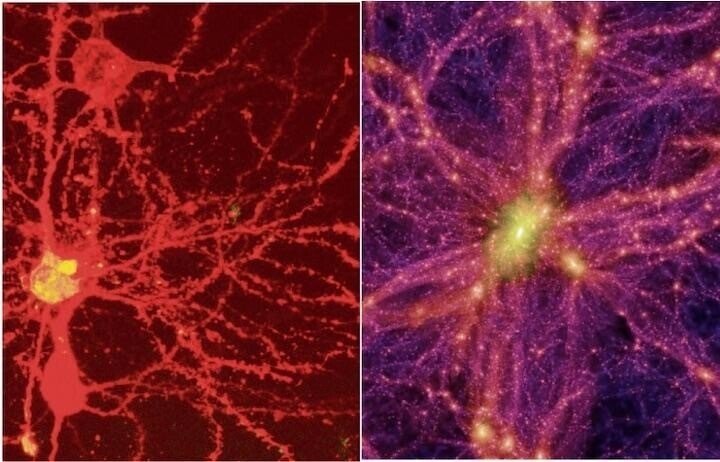
まさに「As above so below(上の如く、下も然り)」
マクロもミクロも同じ「自然界を構成する黄金比(1:1.618…)」が律(ルール)となっています。
おわりに
本日の記事は以上になります。
黄金比(1:1.618…)をざっくりではありますが説明をしてきました。
記事の最後まで読んでくだり、誠にありがとうございます。
私たちの住む世界を構成する黄金比(1:1.618…)。
マクロもミクロも同じ黄金比が顕れていましたね。
黄金比は、自然界に存在するものに顕れる共通の証であり、印(しるし)です。
銀河も、惑星も、天候も、植物も、動物も、そして人間も、同じ黄金比という印を持っています。
その様なことを知ると、そんな自然がどこか愛おしくなりませんか?
「みんな同じなんだなー」と。私は愛おしくなりますw
そして、この記事で紹介した様な智慧を理解した時に感嘆としてしまいます。
理解することの喜びを感じてしまいます。
では、レオナルド・ダ・ヴィンチの言葉を借り、この記事を終わりたいと思います。
「最も高貴な娯楽とは、理解する喜びである」
「理解するための最良の手段は、自然の無限の作品を十分に鑑賞することである」

ご意見・質問などあれば、お気軽にTwitterにてメール下さい。
※無断での引用・転載禁止※
本記事を引用・転載されたい方はTwitterにてメールして頂けましたら対応します。
noteプロフィールにあります、Twitterアイコンからどうぞ。
