【第3章測定】練習問題3.9.1「 同性婚に関する意見の変化再考」
1.データセット
・第3章の練習問題を解く際に使うデータセットは、以下のリンク先からダウンロードできる。
2.練習問題3.9.1「同性婚に関する意見の変化再考」
(1)【研究1】コントロールグループの回答の相関係数
①第1波調査と第2波調査の回答の相関係数は約0.997
②第2派調査の回答の内、殆どが第1波調査と同じ回答になっている
> gayreshaped <- read.csv("gayreshaped.csv")
> ccap2012 <- read.csv("ccap2012.csv")
> dim(gayreshaped)
[1] 11948 6
> summary(gayreshaped)
study treatment therm1
Min. :1.000 No Contact :6441 Min. : 0.00
1st Qu.:1.000 Recycling Script by Gay Canvasser :1046 1st Qu.: 48.00
Median :1.000 Recycling Script by Straight Canvasser :1039 Median : 52.00
Mean :1.204 Same-Sex Marriage Script by Gay Canvasser :2389 Mean : 58.43
3rd Qu.:1.000 Same-Sex Marriage Script by Straight Canvasser:1033 3rd Qu.: 84.00
Max. :2.000 Max. :100.00
therm2 therm3 therm4
Min. : 0.00 Min. : 0.00 Min. : 0.00
1st Qu.: 45.00 1st Qu.: 44.00 1st Qu.: 44.00
Median : 55.00 Median : 57.00 Median : 58.00
Mean : 58.68 Mean : 59.72 Mean : 59.76
3rd Qu.: 84.00 3rd Qu.: 85.00 3rd Qu.: 85.00
Max. :100.00 Max. :100.00 Max. :100.00
NA's :1351 NA's :9835 NA's :9777
> dim(ccap2012)
[1] 43998 3
> summary(ccap2012)
X caseid gaytherm
Min. : 1 Min. : 1.0 Min. : 0.00
1st Qu.:11000 1st Qu.: 251.0 1st Qu.: 45.00
Median :22000 Median : 501.0 Median : 54.00
Mean :22000 Mean : 500.5 Mean : 58.71
3rd Qu.:32999 3rd Qu.: 751.0 3rd Qu.: 85.00
Max. :43998 Max. :1001.0 Max. :100.00
NA's :3097
> cor(gayreshaped$therm1[gayreshaped$study == 1 & gayreshaped$treatment == "No Contact"],
+ gayreshaped$therm2[gayreshaped$study == 1 & gayreshaped$treatment == "No Contact"],
+ use = "complete.obs")
[1] 0.9975817(2)【研究2】コントロールグループの全回答の相関係数
・コントロールグループの第1〜4波調査の回答の相関係数は、
最低でも約0.9308と非常に高い値になっている。
> gayreshaped_2 <- gayreshaped[gayreshaped$study == 2 & gayreshaped$treatment == "No Contact",c(3,4,5,6)]
> cor(gayreshaped_2,use = "pairwise.complete.obs")
therm1 therm2 therm3 therm4
therm1 1.0000000 0.9734449 0.9594085 0.9709017
therm2 0.9734449 1.0000000 0.9308287 0.9436621
therm3 0.9594085 0.9308287 1.0000000 0.9343249
therm4 0.9709017 0.9436621 0.9343249 1.0000000
> min(cor(gayreshaped_2,use = "pairwise.complete.obs"))
[1] 0.9308287(3)【研究2】コントロールグループの全回答の散布図
・高い相関係数が示すように散布図も外れ値が少なく、45度線付近に
分布している
> install.packages("psych")
> library(psych)
> psych::pairs.panels(gayreshaped_2)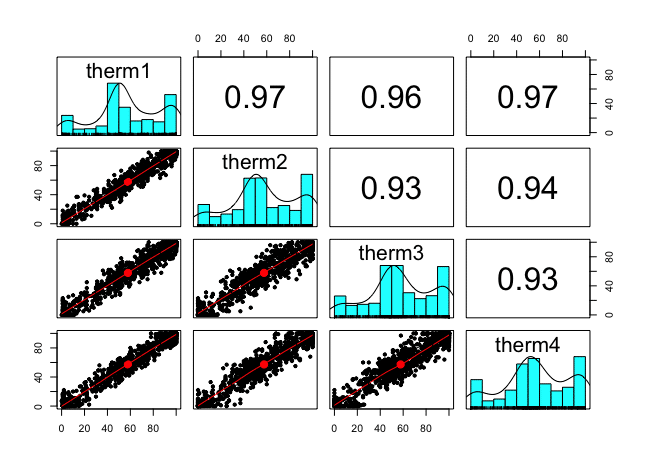
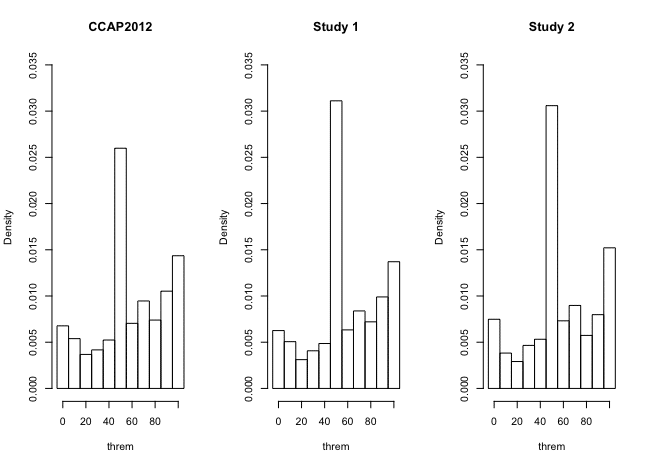
(4) 【CCAP2012】データと【研究1】&【研究2】データの比較(A)
①2つの標本における第1波調査回答のヒストグラムの形状は概ね同じ
②最頻値の密度【CCAP2012】より【研究1】&【研究2】の方が高い
③【研究1】&【研究2】は、【CCAP2012】の欠損値を最頻値で補正
して作成された可能性がある。
> summary(ccap2012$gaytherm)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.00 45.00 54.00 58.71 85.00 100.00 3097
> summary(gayreshaped$therm1[gayreshaped$study == 1])
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 48.00 52.00 58.38 84.00 100.00
> summary(gayreshaped_2$therm1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 47.00 51.00 57.89 83.00 100.00
> par(mfrow = c(1,3))
> hist(ccap2012$gaytherm,freq = FALSE,
+ breaks = seq(from = -5,to = 105, by =10),ylim = c(0,0.035),xlab = "threm",main = "CCAP2012")
> hist(gayreshaped$therm1[gayreshaped$study == 1],freq = FALSE,
+ breaks = seq(from = -5,to = 105, by =10),ylim = c(0,0.035),xlab = "threm",main = "Study 1")
> hist(gayreshaped_2$therm1,freq = FALSE,
+ breaks = seq(from = -5,to = 105, by =10),ylim = c(0,0.035),xlab = "threm",main = "Study 2")
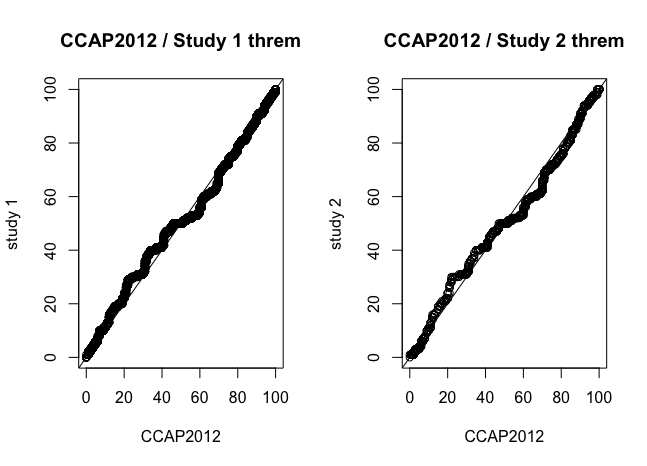
(5)【CCAP2012】データと【研究1】&【研究2】データの比較(B)
> par(mfrow = c(1,2))
> qqplot(ccap2012$gaytherm ,gayreshaped$therm1[gayreshaped$study == 1],xlim = c(0,100),ylim = c(0,100),xlab = "CCAP2012",ylab = "study 1",main = "CCAP2012 / Study 1 threm")
> abline(0,1)
> qqplot(ccap2012$gaytherm ,gayreshaped_2$therm1,xlim = c(0,100),ylim = c(0,100),xlab = "CCAP2012",ylab = "study 2",main = "CCAP2012 / Study 2 threm")
> abline(0,1)
3.練習問題を解いた感想
・散布図行列の描画方法を調べたところ「psych」パッケージを知った。シンプルにpairs関数でも散布図行列は作成できるが、このパッケージを使った方が、ヒストグラムや相関係数も合わせて記載できて便利だった。
・参考にさせて貰ったサイトを見ると、他にも興味深い描画方法がある。今後も練習問題を解く際に活用してみたい。
この記事が気に入ったらサポートをしてみませんか?
