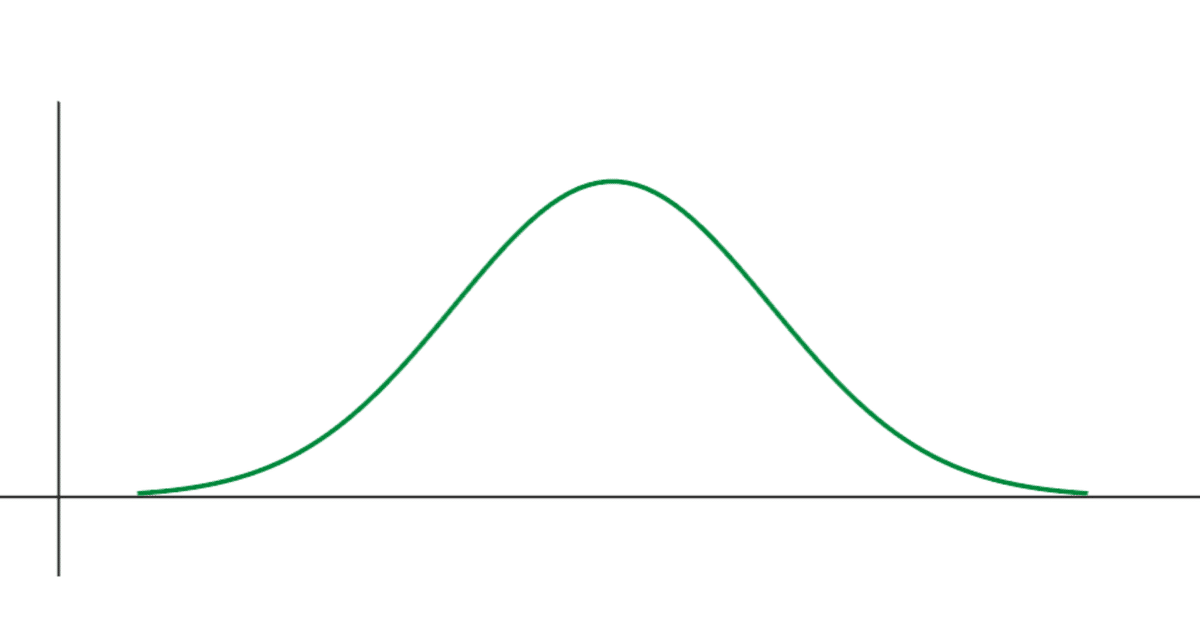
【Illustrator JavaScript】確率密度関数を描く

Adobe Illustrator で可視化シリーズです。
今回は確率密度関数を描いてみたいと思います。

JavaScript 内で確率密度を算出することもできなくはないですが、他のツールで算出した結果を読み込むほうが安全・確実なので Python の Scipy.stats モジュールを使っていきます。

1. 確率密度の算出

Python スクリプト

import numpy as np
from scipy import stats


prob_x = np.linspace(-3, 3, 100)
prob_y = stats.norm.pdf(prob_x, loc=0, scale=1)
prob_xy = np.stack([prob_x, prob_y], axis=1)
np.savetxt('norm_prob.csv', prob_xy, delimiter=',')

-3 から 3 までの範囲を 100 等分した値を横軸に取り、それぞれの位置に対応した標準正規分布の確率密度を算出しています。

出力したファイルの中身はこのようになっています。

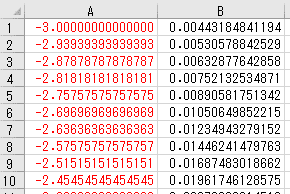
1 列目が横軸の値、2 列目が縦軸の値になっています。

2. 確率密度関数の描画

JavaScript

// 新規ドキュメント作成
app.documents.add(DocumentColorSpace.RGB, 800, 600);


// RGBカラーを設定し、カラーオブジェクトを返す
function setRGBColor(r, g, b) {
   var RGB = new RGBColor();
   RGB.red = r;
   RGB.green = g;
   RGB.blue = b;
   return RGB;
}


// x_margin
var x_margin = 400;

// y_margin
var y_margin = 200;

// 横方向の拡大率
var x_rate = 80;

// 縦方向の拡大率
var y_rate = 400;


// x軸
var xAxisPos = [[-4, 0], [4, 0]];
var xAxisObj = activeDocument.pathItems.add();
xAxisObj.setEntirePath([
   [xAxisPos[0][0] * x_rate + x_margin, xAxisPos[0][1] * y_rate + y_margin],
   [xAxisPos[1][0] * x_rate + x_margin, xAxisPos[1][1] * y_rate + y_margin]
]);
xAxisObj.stroked = true;
xAxisObj.strokeWidth = 0.8;
xAxisObj.strokeColor = setRGBColor(0, 0, 0);

// y軸
var yAxisPos = [[-3.5, -0.1], [-3.5, 0.5]];
var yAxisObj = activeDocument.pathItems.add();
yAxisObj.setEntirePath([
   [yAxisPos[0][0] * x_rate + x_margin, yAxisPos[0][1] * y_rate + y_margin],
   [yAxisPos[1][0] * x_rate + x_margin, yAxisPos[1][1] * y_rate + y_margin]
]);
yAxisObj.stroked = true;
yAxisObj.strokeWidth = 0.8;
yAxisObj.strokeColor = setRGBColor(5, 5, 5);


// 曲線用テキストファイル読込
var prob_file = new File("C:\\Users\\mare_ism\\Documents\\norm_prob.txt");
prob_file.encoding = "UTF-8";
prob_file.open("r", "TEXT");
var prob_text = prob_file.read();

var prob_textRow = prob_text.split("\n");

// 確率密度関数の曲線を描画
var lineObj = activeDocument.pathItems.add();
var prob_arrays = [];
for (var i = 0; i < prob_textRow.length; i++) {
   if (prob_textRow[i].length != 0) {
       var prob_rowItems = prob_textRow[i].split(",");
       var prob_array = [prob_rowItems[0] * x_rate + x_margin,
                         prob_rowItems[1] * y_rate + y_margin];
       prob_arrays.push(prob_array);
  }
}

lineObj.setEntirePath(prob_arrays);
lineObj.filled = false; // 塗りを「なし」にする
lineObj.stroked = true; // 線を表示する
lineObj.strokeWidth = 2;
lineObj.strokeColor = setRGBColor(0, 135, 60);

そのままの数値を使うと左下に小さく描画されてしまうので、x_margin, y_margin を使って描画位置を、x_rate, y_rate を使って拡大率を設定しています。

また、横軸と縦軸も適当な範囲で描画しています。

これらの値は描画領域を見ながら調整して下さい。

実行結果

きれいな正規分布の曲線が描画できました。

3. 応用

Scipy.stat モジュールではいろいろな確率分布が扱えるので、そこを差し替えればいろいろな確率密度関数を描画することができます。

ガンマ分布