新型ウイルスと数学と学歴フィルター

0.前置き

こんにちは。新型ウイルスが猛威を振るっており、社会人一日目は自宅学習となりました。この話題に関して一つ気になった事についてまずお話しさせていただきます。

ちょっと前に積極的にコロナ検査をしない理由みたいな内容の記事を見ました。（出典とかは忘れてしまいました。すみません）

検査キットが患者に対して陽性か陰性か正しく判断できる確率が100 %ではなく、加えて検査を受ける人に対して実際に感染している人が少ない場合を考えます。

このとき、検査キットを用いて陽性と判断された人の中で、非感染者であるにもかかわらず誤って感染者と誤認されてしまう人数が、実際に感染している人数より多くなってしまうというものです。

以下に例を示します。

検査キットは95 %の確率で陽性陰性を判断できます。
一方ウイルス感染者は全体の0.1 %です。全体は100000人とします。

このときの陽性と判断された人達の内訳について考えます。
　・本当に陽性かつキットからも陽性と判断された人
　　100000×0.001×0.95＝95人
　・本当は陰性なのに誤って陽性と判断された人
　　100000×0.999×0.05＝4995人

つまり陽性と判断された人4995+95＝5090人中4995人、約98 %は陰性です。つまり陽性と判断された人が実際に陽性である確率（条件付確率）は約2 %ということになります。

検査キットは95 %の精度を持つにもかかわらず、上の計算から出てきた精度は2 %というのは不思議ですよね。（調べたら、ベイズの定理というものらしいです。）

というように。むやみに検査をしてしまうのも考えものというような記事でした。（正直内容はそこまで覚えてないです。確率の計算が印象に残っていたので書かせていただきました。）

上記で出した数字は例なので、実際の精度はもっと高いでしょうし、検査の条件もいろいろあって考えられているとは思います。

私がこの話で伝えたかったのは、いろいろな情報が錯綜しているので何が正しいかはわかりませんが、せめて「こういう考えもあるんだ」というのを感じて、自分の中で何が正しいか考えていけるようになりたい、ということです。ちょっと例が不謹慎かもしれませんが自分自身気を付けていきたいと思っていることです。

と、いろいろ話しましたがここからが私にとっての本題となります。

前回学歴フィルターについてお話ししました。
そこでふと、「優秀な学生の数」を上述の「実際に感染している人の数」に置き換えて考えることができるな、と思いました。

ということで、やってみました。
しかも理系らしく一般化してみました。

1.前提条件

数学の問題を解くときは前提条件が大事です。自分の専門は化学ですが、、、
優秀な学生の定義について考えます。大学の難易度に比例して優秀な学生がいる確率が大きくなると仮定します。要は勉強できるならば優秀である確率が高いと考えています。

次に変数を設定していきます。
a：全学生の人数に対する優秀な学生の割合
　（上の仮定から学歴フィルターをかけて高学歴の学生を増やすほどaは
　　大きくなります）
b：面接官が学生を優秀かそうでないかただしく判断できる確率
　（優秀と判断した場合全員採用すると仮定）

a,bともに確率なので0≦a≦1、0≦ｂ≦1となります。

次に、採用した学生の中に実は優秀でない学生が混ざっている確率を計算します。

2.計算

求める確率をｆ(a,b)とします。受験した学生の総数をSとすると、優秀で
あり採用された人数は、
Sab
となり、逆に優秀でないにも拘わらず採用された人数は、
S(1-a)(1-b)
となります。

よって、

f(a,b)= S(1-a)(1-b) / { S(1-a)(1-b)+Sab }
= (ab-a-b+1) / (2ab-a-b+1)…A

となります。変数二つでわかりにくいですね。ということで、ｂを変数として式変形してみました。

f(a,b)= -a(a-1)/[{(2a-1)^2}{b-(a-1)/(2a-1)}]+(a-1)/(2a-1)…B

(本当はcodeとか使ってきれいに数式書けたらいいんですけどわからないのできませんでした。そもそもnoteでできるのかもわからない。わかる人いたらコメントなどで教えていただけると嬉しいです)

無理やり変形して反比例の一般式にするところまで来ました。

3.場合分け、グラフ

この後、どうしようか迷いました。グラフを書こうにも2変数なので3次元のグラフは作れないし（excelでできたかも）、a,bそれぞれで偏微分してぐちゃぐちゃするのは能力的に無理だし、、、

ということでｂを固定してグラフを書くことにしました。が、Bの式ではa=0.5のとき分母に∞×0ができてしまいうまく計算できませんでした。なんでダメなのかはわかりませんが、たぶんAからBに式変更する際（2a-1）を作ってしまったためと思われます。なんでダメかわからなかったので式変形ミスを考えましたがミスってなかったので更に悩みました。で、悩んだ結果場合分けすることにしました。
（AからBの変形ミス、もしくは場合分けがあっていた場合場合分けが必要になってしまった理由を教えていただけますとありがたいです。にわかですみません）

場合分けは、Aにあてはめ計算し

f(1,b)=0
f(1,0)=1
f(0.5,b)=-b+1
f(0,b)=1
f(0,1)=0　＊このときは優秀な学生が0人のため採用人数0人となりますが、優秀でない学生を採用しなかったと考え”0”としました。

として、それ以外の時はBの式を用いました。以下結果です。

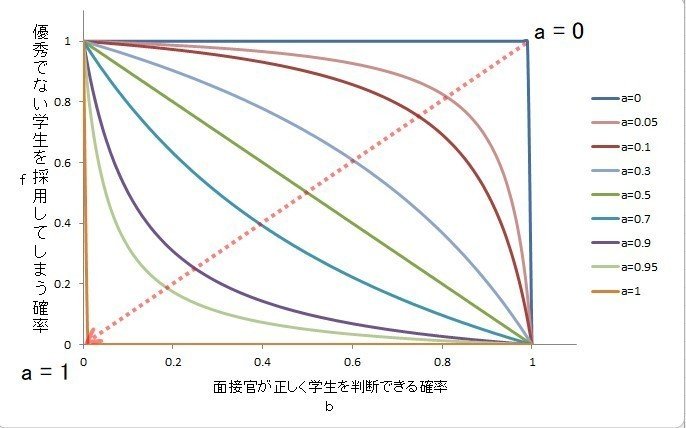
各aの値の時のグラフを書きました。グラフから、二点（0,1）(1,0)は必ず通ることがわかります。

b = 0.8として線を引いて、確率を比較してみました。

このことから、仮に面接官の精度が80 %であった場合積極的に学歴フィルターを使った場合（a = 0.95）と使わなかった場合（a = 0.05）で約80 ％強の精度の差が出てしまうということがわかりました。

＊グラフはエクセルで作りました。なぜか貼り付けたら画質が悪くなりました。

ということで、学歴フィルターを使うメリットを数学的に説明してみました。

もしかしたら、すでに同じようなことをしている人もいるかもしれませんが少しでも面白いと思っていただければ幸いです。（書いてるうちに、理系の気持ち悪さが出てるなぁとも思いました。）

もちろん、今回は様々な仮定をしているので絶対に正しいとは限りません。

そして、途中途中に書いた質問に答えられる方や、ミスを発見した人などいましたらコメントをいただけるとありがたいです。

今回は、理系らしくレポートのようなものを書きました。社会人一日目に何を血迷ったのかはわかりませんが、楽しんでいただけたでしょうか？

最後までご覧いただきありがとうございました。

＊重ねて保険を張りますが、自分は化学専門のため温かい目で見て頂ければ幸いです。