新型コロナウイルス感染隔離後の感染者の動態モデルとそれに基づく簡易計算の試み

厚生労働省のウエッブサイトに、新型コロナウイルス感染症に関する日々の発生状況を示すオープンデータが開示されている。主要な項目は、１．陽性者数（新規感染者数）、２．入院治療等を要する者の数（重症者を含む現在の感染者数）、３．退院または療養解除となった者の数（積算の回復者数）、４．死亡者数（累積数）、５．重症者数（集中治療室(ICU)、人工呼吸器(Ventilator)、体外式膜型人工肺(ECMO, Extracorporeal Membrane Oxygenation)を使用している者の数）である。

当然のことながら、上記の各項目の数字には若干の問題点が含まれる。例えば、１）一旦P C R陰性となって回復した患者が再陽性となった場合の取り扱いに一貫性がない、２）重症者の定義が各都道府県によって異なる、３）現在の感染者数は、新規感染者総数−それまでの回復者総数−死亡者総数から計算される数値と完全には一致しない（収支が取れない）、などである。

以上のような曖昧さはあるが、新型コロナウイルス感染者が隔離されたのちの人々の動態を、a) 重症者を除いた、（病院や自宅、指定ホテルで）療養中の患者のグループ、b) ICUやECMOを利用している重症者のグループ、c) PCR検査が陰性となり回復した人々のグループ、d) 不幸にして亡くなった方々のグループ、以上の４つのグループ（コンパートメント）に分けて考えることができる。これを模式的に書くと以下のようになる。

ΔQは毎日の新規感染者数である。感染者Qは病院や自宅で療養し、やがて回復してRとなる。一部の患者は重症化し、ECMOなどを必要とする重症者Seに移行する。重症者はある期間の救命措置を施されて一般患者Qに戻る。しかし、一部の重症者は死亡するD。また、一般の患者Qも容態が急変し死亡に至るケースもある。

以上の４つのコンパートメント間移動過程の速度定数を、順に、ε(Q → R)、κ(Q → Se)、ρ(Q ← Se)、δ(Se → D)、ξ(Q → D)とする。

各コンパートメントの人口収支式は以下のように書かれる。

上式の計算は、時間幅を１日とした差分式に置き換えることができる。QとSeの初期値は2020年9月30日の現在感染者数と重症者数の各7日移動平均値を与えた。なお、日々の新規感染者の流入速度ΔQは新規感染者数の７日移動平均とした。

計算の対象期間は第３波とし、2020年10月1日から2021年2月25日までの約５ヵ月間のデータを用いた。この間の新規感染者数ΔQと実効再生産数Reの推移を次の図に示す。

上式で変数は４個あるが、独立なのは３個である。しかし、パラメータは５個ある。最適パラメータの決定には非線形最小二乗法が必要であるが、私はこのプログラムは所有していない。そこで、エクセル上での各変数の計算値が、相当する７日移動平均のデータと、より一致するように目視でパラメータ調整を行った。

もしこれが学術研究であれば許されないと思うが、当該分野の専門家でもない私個人の興味に基づく計算に過ぎないので、どうかご容赦いただきたい。

以下の５枚のグラフは、パラメータ値を ε = 0.08、κ = 0.004、ρ = 0.2、ξ = 0.001、δ = 0.03 （単位はすべてdayの逆数）としたときの計算線とデータの比較である。

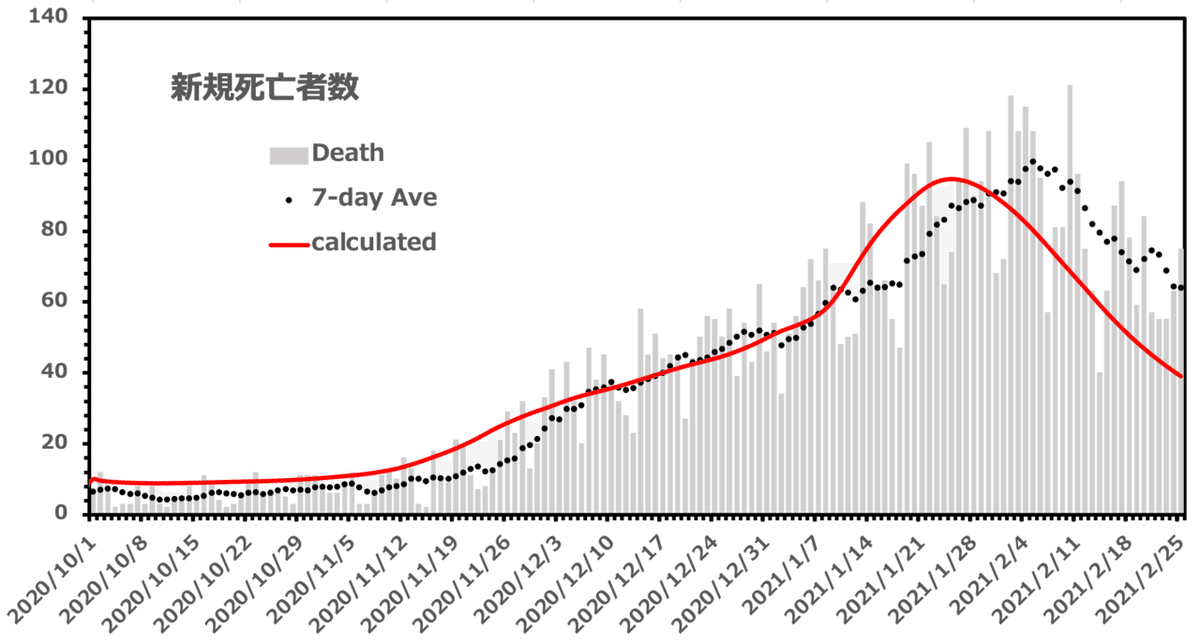
パラメータ値が最適化されたものではないことを考慮すると、モデル計算の結果は大雑把に見て実際のデータの傾向をうまく表現していると言える。しかし精細に眺めると、計算線はデータからかなり偏奇している。現在の感染者数については、今年１月以降のズレが大きく、とくに１月下旬以降の計算線は実際より多くの感染者数を示している。重症者数についても１月の下旬以前と以降では計算線とデータの大小関係が変わっている。新規死亡者数については、モデル計算のピークの位置が実際のデータより10日ほど早く現れている。

冒頭に記述したように実際のデータについても曖昧な点があるが、モデルについても多くの問題点を含んでいる。最も大きな点は、本モデルは均一化・非構造化モデルにすぎないということである。とくに若年層には無症状感染者が多く、高年齢層ほど重症化し易く、かつ死亡率も高いと言われる。このような年齢による分布を考慮した構造化モデルが実際のデータをもう少しうまく説明するかも知れない。

最後に、新型コロナウイルス感染症でお亡くなりになった方々に対しまして、心からお悔やみを申し上げますとともに、現在感染中の方々には一刻も早いご回復を祈念申し上げます。