三角関数の加法定理の導出
幾何学的導出
高校数学で習う三角関数は次のように定義される.
![]()
図で表すと,

三辺の長さの比は角度θが求まれば決まってしまうという優れもの.
例えば建物の高さを知りたいとき,建物までの距離(x)と,角度(θ)が分かっていれば高さyはx*tan(θ)で求まる.幸いにも先人の研究のおかげで三角関数表があるのでそれを見ながらあとは電卓で計算すればよい.
では本題へ行こう.
角度αの三角形に角度βを加えると緑太線で囲まれた三角形となる.
この三角形のsin(α+β),cos(α+β),tan(α+β)をsin(α),cos(α),sin(β),cos(β),tan(α),tan(β)で表すことを考えよう.

答えからいうと三角関数の加法定理は次のようになる.
![]()
![]()

まず,次のように補助線を引く.

これから三角形の辺の長さがsin(α),cos(α),sin(β),cos(β)を用いて次のように表せる.

これからsin(α+β)は,次のようにして求まる.
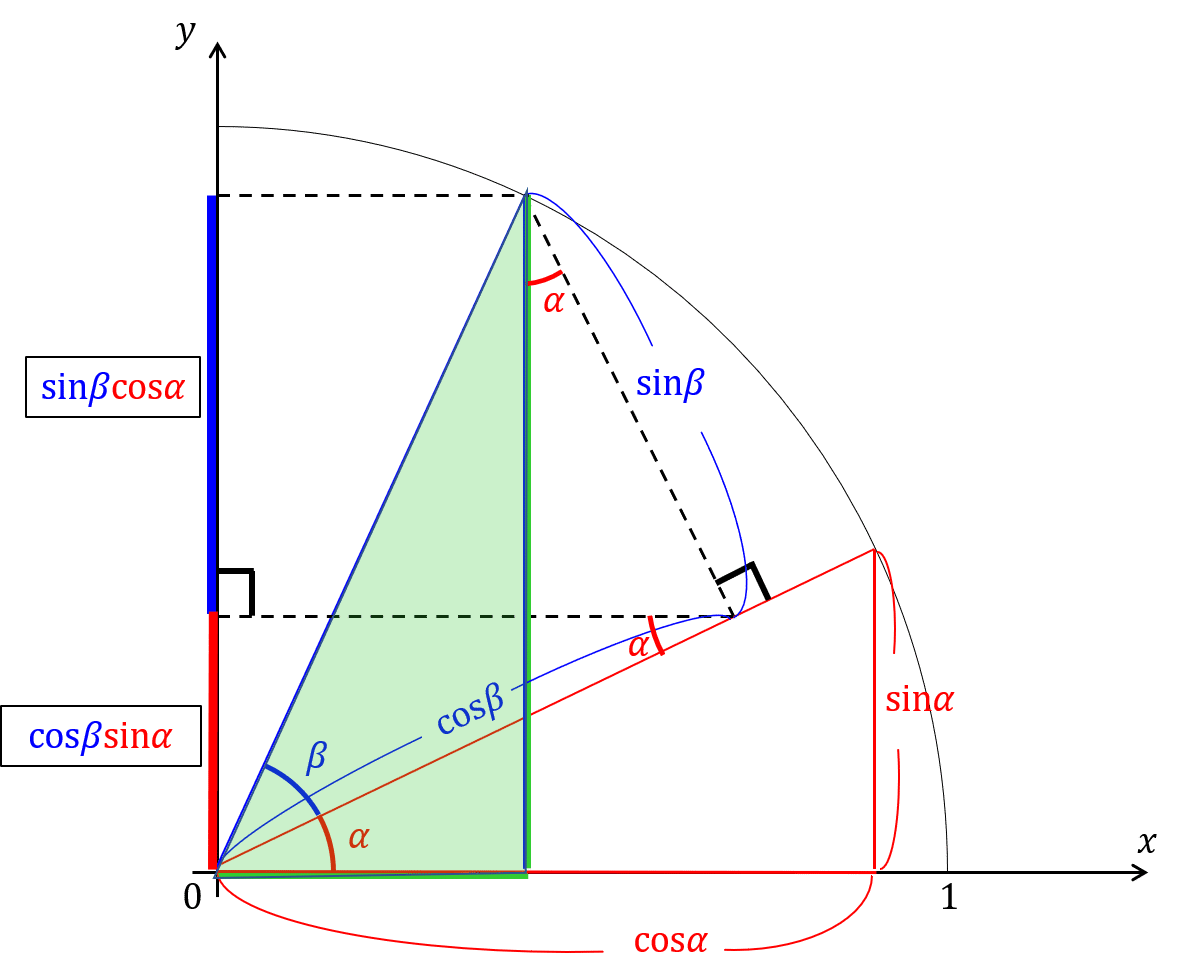
cos(α),cos(β)を斜辺とする直角三角形を取ると,sin(α+β)は赤太線と青太線の和となるので,
![]()
が求まる.
同様にして,cos(α+β)は,
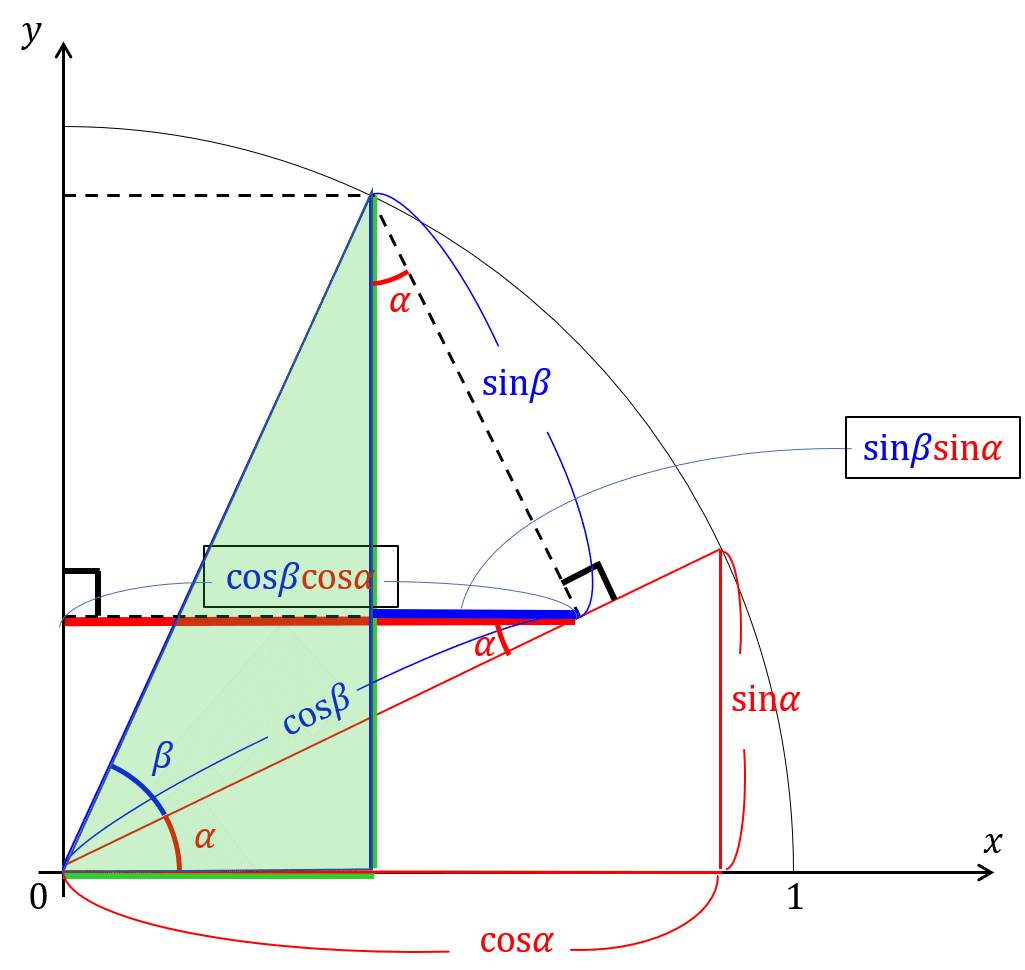
赤太線から青太線を引いた長さがcos(α+β)となる.
![]()
tan(α+β)はtanの定義から求められる(簡単な計算なので求めてみるとよい).
別の導出方法としてド・モアブルの公式(複素数平面)を使った方法があるが,
今回はここまで.
