
なんで授業範囲外の勉強しようって思うの?②
前回に引き続いて「は?何こいつ、授業でもねーのに勉強してんの?怖いわ〜」という印象を持たれている方に釈明する意味も込めて、授業範囲外の勉強をする動機を挙げてみようと思います。
前回は「好奇心」「新しいことを学んだ時の衝撃」という、結構内面的な話題でしたが、今回はもっと切実な悩みにも応えられるようなことを取り上げましょう。
なんで?→役立つ
「学校の勉強が役に立つ」という言葉ほど無責任なものはありませんよね。「サインコサイン何使うん?」ですよ。もちろん理系大学生として正弦余弦の便利な使い道の一つや二つは当然の如く存じ上げておりますが、世の少年少女が思い描いている「役に立つ」とは、比べられる代物ではないでしょう。
自分はここ最近簿記会計だったりプログラミングだったりとした勉強をしていますが、最初の動機には好奇心もありますけど、それ以上に将来役に立ちそうという理由があってモチベーションを維持できていると思います。目に見えて自分の今後に関わってくるスキルを勉強するとなると、やはり熱が入りますね。
「簿記とか将来使わねーよ」
例えが若干悪かったでしょうか。そしたら所得税の計算なんかはどうです?「あといくら稼いだら扶養控除が受けられなくなって、家族全体の収入がいくら減るから、今月はこれ以上稼いじゃいけない」みたいな計算、将来とは言わず今でも使いませんか?あらあら、こんなところでネットサーフィンなんかしてて、税金の勉強しなくていいんですか?
なんで?→暗記しなければいけないことが減る
これは特に受験生なんかにウケがいいでしょうね。いやいや、ウケ狙い一筋で文章書いてんじゃないですよ、誤解ですって。でも実際「そんな意味のない『公式』暗記しなくたっていいのに」なんて言われたら、嬉しくないですか?
微積物理が最たる例でしょう。「基礎」が付いていない物理の話にはなりますが、交流のリアクタンスをベクトル図で考えるなんて、そんなもん絶対覚えられませんって。それに忘れたらどうしようもないじゃないですか。例えばこんな場合を考えてみましょうか。

例のベクトル図なるものを描いてみましょうかね。

ベクトル図あってますかね?ちょっと自信ないんですが、確か R に対して L が先行してるんでしたよね。まあ、このまま数式にしてみます。
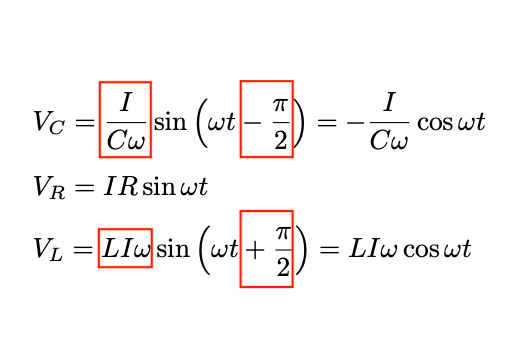
式の赤いところは暗記しないといけないと言われるところです。多くね?こんなん覚えられるわけないだろ。
大学で電磁気やれば、これがいかに不要な暗記だったかもわかっていただけると思います。だってコンデンサーの特性やコイルの自己インダクタンスの式に従って微分方程式立てるだけですから。
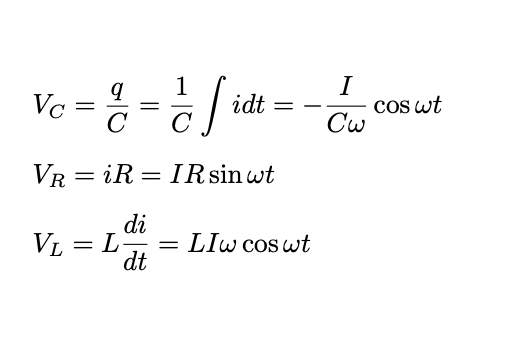
1本目は「Q=CVの式変形」と、「蓄積しているでんかは電流の時間積分で表せる(∵電流は電荷の時間微分)」という、それなりに重要な性質をそのまま書き出しただけ。2本目はオームの法則そのもの。3本目は自己インダクタンスそのもの。新しく覚えなきゃいけないことなんて何もないんですよ。
ただし暗記を全否定するわけではありません。制限時間があるテストで頭使う時間を減らせるというメリットがありますから、受験に暗記はつきものです。が、こんなことまで覚えなくていいんじゃないの?って話。
なんで?→やっておくと大学で楽
別に高校時代にこんなモチベーションがあって勉強してたわけじゃありませんが、大学入った今になってみれば指導要領外の勉強しっかりしておいてよかったなーと思います。
高校数学の教科担任が結構厳密な先生で、極限についての説明をするときは、もちろん単純に「nを無限大に飛ばしたら…」なんて表現を普段は使いましたけど、そのあと必ずイプシロン-デルタ論法というものに触れていました。僅かに触れていただけなので、大体の生徒はスルーしていたのですが、自分はちょっと気になったので勉強してました。
このイプシロンデルタ論法、理系の大学1年生ならまず避けては通れない話なのですが、高校でやっていたおかげで入学直後から快調なスタートダッシュを切ることができたと言っても過言ではないでしょう。
「イプシロンデルタってなんじゃい」と思った方、ちゃんと最後の[補足]で説明しますよ。数学では引っ張りだこの話で、教科書や授業の至る所に出てきます。微積分学の授業でこの話を聞かない日はありませんね。
もちろん高校生の間にこんな勉強する義理もヘッタクレもありません。が、大学生となった今からしてみれば、勉強しておいて本当によかったと思っています。
なんで?→普段の勉強から逃げられる
「いやいや、なんで勉強から逃げるために勉強してんだよ」って思いました?思いますよね~。でもテスト前とか受験前みたいに勉強しなきゃいけないときに、「勉強してるからいいじゃ~ん」てな具合に現実逃避する言い訳になるって意味で、テストや受験に全く関係ない勉強するのはオススメです(オススメしてはダメなんですが)。
テスト期間を例にすれば共感してくれる人が多いかもしれません。テスト期間ってテスト範囲と全く関係ない勉強捗りませんか?
自分の場合だと、高校理科は物化選択だったのですが、友人にめっちゃ生物教えるのが上手いやつがいて、テスト前はそいつにDNAの複製メカニズムとか教わってました。テスト勉強に疲れた高校生にとって、トリマーRNAだの、バージェス動物群だの、あんなに面白い授業はありませんでしたね。
大学入ってからも、テスト期間にベートーベンの歓喜の歌をドイツ語から全訳しましたが、もうその頃には第二外国語のドイツ語の成績はとっくに決まっていたし、来期はラテン語取ろうと思っているので、もはや何の利にもならない。「全くなんで電磁気や微積分そっちのけでこんな勉強してるんだろう」なんて思いながらも、やっぱりやめることはできず完訳しました。そのムダな努力の結晶は note
にあげてますので、ぜひご覧ください。また、10回 manabo というシステムを使ってお教えすることも可能です。近日完訳した「紅蓮の弓矢」のドイツ語部分
https://note.com/teion_burns/n/ncddf44de31a5
と合わせてご検討ください。
さて、普段の勉強から逃げられる話に戻りましょうか。
他にも自分が浪人していたとき、冬になってどうも勉強のやる気が出なくなったことがありました。1年半も受験生やってるもんだから、受験勉強つまんなくなるんですよ。でも仮にも浪人生です。勉強しないで遊び歩くわけにもいかない。
そこで受験生、なんと丸善でイタリア語の教科書を購入、嬉々として勉強しました。「なんでイタリア語?」と思われたことでしょう。高校時代の英語の教科担任にこんなことを言われた背景があってのことです。
「日本人がヨーロッパの言語やるんだったら、まずはイタリア語やるべき。まず発音がほとんど日本語と同じ。語形変化も少ない。」
そんな話があったもんだから、「ちゃんと勉強してるんだし、文句ねーだろ」ということで突飛な逃避行を決行したわけです。お受験なんてやってられっかってんだ。ちなみに大学に入ってもなお、ベートーベンの全訳が終わってからは浪人の冬に買った例の教科書にお世話になっています。もちろんこれもテスト期間内に。「ちゃんと勉強せぇよ」って?いやいや、どこからどう見たって勉強してるじゃないですか。
まとめ
今回は授業外範囲の学習をするモチベーションを、眼に見える形で得をするという点を強調してご紹介しました。もちろん前回ご覧に入れたような「役に立たなくても楽しい」という側面はありますが、それだけだとどうしても勉強が続かないという方も多いことでしょう。「実用的」ということをうまく折り込んであげれば「しゃーねーな、将来のために勉強するか」といった形でちゃんと勉強するモチベーションにつながりますから、ぜひ参考になさってください。
[補足] イプシロンデルタ論法
まずは高校で極限をどうやって説明するかというところからおさらいしてみましょうか。
「関数 f(x) において、x が a と異なる値を取りながら a に限りなく近づくとき、f(x) が一定の値 α に限りなく近づく場合、『x が a に近づくとき f(x) は α に収束する』という」
わかりやすいように f(x) = x+1 を考えてみましょう。x が 1 に限りなく近づくとき、当然 f(x) は 1+1=2 に限りなく近づきますから、「x が 1 に近づくとき、f(x) は 2 に収束する」と言えます。なるほど非常にわかりやすい定義だ。
でも大学の微積分はこんなチンケな表現では許してくれません。厳密に客観的に定義しようとするあまり、数学者連中はこんな言い方を思いついてしまったのです。
「任意の正数εに対して 0 < |x - a| < δならば |f(x) - α| < εとなるような正数δが存在する場合、『x が a に近づくとき f(x) は α に収束する』という。」
一回りも二回りもして「???」となりかねない定義ですが、これこそ大学数学では一般的な定義になります。定義の中でε, δといったギリシャ文字が出てきますが、それぞれ「イプシロン」「デルタ」と呼ぶので、「イプシロンデルタ論法」という名前がついています。まったく、こんなこと書いてるから理系志望が減るんだよ。
