
ベイズ統計学を直感的に理解しよう!オオカミ少年はなぜ信用されなかったのか数学的に解説します
スタンダードな統計学では、結局、データがたくさんないと、正確な結果が出せない。
でも、そんな時間も予算もないし、少ないデータでも、「統計的な有意差があるレベルのデータ数は集められてないけど、今のところこれが有力!」くらい言えるようになりたい、というワガママを叶えてくれるのが、ベイズ統計学です。
結構いい加減な統計学なのですが(詳細は後程解説します)、
人間の思考プロセスと近い性質を持っていて、
現在、実務の世界ではかなり普及しています。
迷惑メールフォルダ振り分け機能、検索エンジン予測変換機能、OSのヘルプ表示機能、ECサイトの1to1マーケティング(おススメ商品表示機能)
などに使われている技術です。
ベイズ統計の強みは・・・
・データが少なくても推測でき、データが多くなるほど正確になる。
・入ってくる情報に瞬時に反応して、推測をアップデートする。
ので、
◎より少ない情報で意思決定する実用的な統計学
◎難しい分析手法は使わず、四則演算でできる。
ってとこでしょうか。
まあ、概念の説明よりも、
実際にどんなことをするのか、見てみましょう。
動画で見たいかたはこちら
「オオカミ少年のベイズ推定モデル」
ベイズ統計学の考え方を使って、推測することを、「ベイズ推定」と言います。
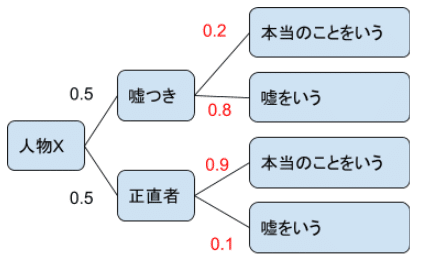
・今、目の前に初対面の人(人物X)がいるとします。
・その人が、嘘つきか正直者かどうか見極めたいとします。
初対面なので、その人がどういう人なのかは分かりません。
なので、とりあえず、人物Xが、嘘つきである確率と、正直者である確率を、半々(1:1=0.5:0.5)に設定します。

※主観的に決める確率なので、これを「主観確率」と言います。
このように、だいたいこのくらいの確率だろう、と事前に決めておく確率のことを、「事前確率」と言います。
もうすでに、いい加減でしょう?(笑)
でも、これでいいんです。理由は後で説明します。
・嘘つきが、本当のことをいう確率が、0.2。嘘をいう確率が、0.8だとします。
・正直者が、本当のことをいう確率が、0.9。嘘をいう確率が、0.1だとします。
※これを、「条件付き確率」と言います。
条件付き確率は、事前アンケートや、既存データから事前に計算しておきます。
それで、
今、その人が、《一回嘘をついた》という情報が得られたとします。
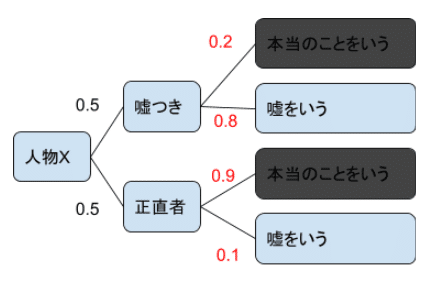
そうすると、
可能性としては
(1)嘘つきで、嘘を言った可能性と、
(2)正直者で、嘘を言った可能性、
この二つが存在しますよね。
この時の確率を求めてみましょう。
(1)嘘つきで、嘘を言った確率
→事前確率0.5×条件付確率0.8=0.4
(2)正直者で、嘘を言った確率
→事前確率0.5×条件付確率0.1=0.05
(1):(2)=0.4:0.05=8:1
になります。
嘘つき:正直者=8:1
ということですね。
この8:1というのは、正確には確率ではなく、
オッズ比と言います。
「確率は、足して1になる。」が原則なので、
これを、足して1になるように計算してみましょう。
嘘つき:正直者=8:1
=8/9:1/9
=0.888:0.111
≒0.9:0:1
嘘つき:正直者=0.9:0:1
になるので、
情報が何もない状態で、嘘つきである確率は、50%だったものが、
一回嘘をついたことにより、
その人が、嘘つきである確率は、90%に変化した。
ということになります。
情報を入れたことによって、
変化した確率のことを「事後確率」と言います。
このように、事前確率から事後確率に変化することを、
ベイズ更新と言います。
さらに、人物Xが、もう一回嘘をついたとしましょう。

そうすると、
ベイズ更新後の事後確率は、いくつになるでしょうか?
嘘つき:正直者
=0.9×0.8:0.1×0.1
≒0.99:0.01
になり、嘘つきである確率は、99%になります。
このように、
最初に、えいや!で主観的に確率を設定したとしても、
逐次、観測データを入れて、ベイズ更新して、事後確率を修正していくと、
最終的には、スタンダードな統計学で出した結論とほぼ等しくなります。
実はここが一番、実務で使い勝手のいいポイントなのです。
従来の統計解析では、
一度、溜まったデータをまとめて解析にかけて、結論をだし、
また、情報が溜まってきたら、解析にかけて、、
みたいな感じで、手間暇をかけて分析していました。
しかし、ベイズ統計の場合は、情報が入るたびに、ベイズ更新されて、
即座に確率計算されるので、また全データを解析にかけ直す、という手間がいらなくなったんですね。
これは、
分析者からすると、
かなり画期的なことなんです。
ビッグデータのように、常に増え続けるデータの場合、人間の手でデータ収集→解析→モデル修正するのは、現実的に追い付かないんですよ。
しかも、たくさんデータを保管しておくと、サーバーがパンクしてしまうこともあるので、データの保管の点からしても、使い勝手がいいんですね。
なぜなら、情報が入るたびに、事後確率が更新され続けるので、その情報さえあれば、個別の情報は忘れてしまっても、問題ないからです。
おお、なんて省エネなんでしょう。
モデル自体が、情報が入るたびに学習し続けるので、まさに、AIの基礎モデルなんですな~。
「答えは分からんから、仮に決めて、やってみて、修正し、現時点で確率の高い方を選択する。そのループを回す」
というベイズの考えた方が、合理的で、奥が深くて私は好きです。
ベイズ推定は、人の思考回路と似ているとも言えます。
例えば、
あなたが、忘れ物を見つけたとして、
可能性としては、AさんかBさんのものだとしましょう。
もし、Aさんが、忘れっぽい人であれば、
「多分、Aさんのじゃね?」
って判断しますよね?
忘れ物の持ち主が、AさんかBさんである確率を、《よく忘れ物をするはどちらか》という過去の観測事象から、推定しているからですね。
スタンダードな統計学とベイズ統計学で、共通する考え方に、「最尤(さいゆう)原理」があります。
これは、「世の中で起きていることは、起こる確率の高いことである。」という考え方です。
神様によって、あらかじめ確率が決められているとしたら、
実際には、確率の高いものから観測されるだろう。
ってことですね。
この考えた方が面白いなと思い、
私が、統計と確率の違いを説明する時に、
「統計は、《現実》
確率は、《仮想現実》」
っていう例えを用いるのですが、
多分、伝わっていないでしょうね(笑)。
いいなと思ったら応援しよう!

