
②”max-plus代数による鉄道ダイヤ”を利用した”N対N配車問題の解法”など
無料でも、アカウントの過去会話を覚えていてきちんとそっち寄りの話題に合わせてくれるのが嬉しい。私のChatGPTは物流と数学に特化させてるのでね。(生成AIによって使い分けてる)
さて、ペトリネットでイベントグラフというのを作る。
というか、人間はイメージだけすれば、これを描かなくても良い。
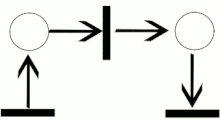
丸が事象であったり場所であったり。線はイベントだ。(ANDとかORとか表現できる)
丸の中にはトークンと呼ばれる●が描かれている場合があって(上の図では無いが)、そこが出発点になる。
(ここまでは6年前に勉強したけど、描いても計算が大変だと思って止めた)
これができれば、後は計算である。ここまで確認できた。(嬉しい)
なんと、配車も動的スケジュールも解決出来るらしい。
今までに、GNNで実現できるのは確認してたけど、機械学習ってXAIもあるけど計算結果を説明しないといけないから躊躇してた。
条件を入力すれば時間付きイベントグラフを描画できますか?
はい、Mermaidを使って時間付きイベントグラフを描画できます。具体的にどのようなイベントと時間を可視化したいですか?例えば以下のような情報があると役立ちます:
1. 表示したいイベントの内容
2. イベントの発生時刻や所要時間
3. イベント間の関係性(並行・直列など)
4. 特に強調したい重要なポイント
これらの条件をお聞かせいただければ、適切なタイムラインやガントチャートなどの形式でグラフを作成できます。
そりゃ、いい。
円形に3駅がつながっています。
電車は各駅に停車中の3つがあります。
仮に1,2,3と名付けます。
電車1以外は、前の電車が駅を出ないと動けません。

恐ろしい事に、生成AIがあるとペトリネットは自分で考える図ではなくて、正確にイメージが伝わっているかどうかを確認するための手段でしか無い。
問題はここからだ。自動的に計算ができないとならない。
この条件をペトリネット風に表現したとして、 これをmax-plus演算を用いて 数式化したいのです。
## 変数定義
### 時間パラメータ
- τₛ: 停車時間(各駅共通と仮定)
- τᵢⱼ: 駅i から駅j への移動時間
- hᵢⱼ: 電車i と電車j の最小追従時間
### 状態変数
x_i^k(n): n回目の運行でのi番目の電車の駅kからの出発時刻
## システム方程式
### 物理的制約(移動時間)
x_1^B(n) = max(x_1^A(n-1) + τₛ + τAB)
x_1^C(n) = max(x_1^B(n) + τₛ + τBC)
x_1^A(n) = max(x_1^C(n) + τₛ + τCA)
### 追従制約
x_2^k(n) = max(x_2^k(n-1) + τₛ + τₖₖ₊₁, x_1^k(n) + h₁₂)
x_3^k(n) = max(x_3^k(n-1) + τₛ + τₖₖ₊₁, x_2^k(n) + h₂₃)
### 行列形式
```
⎡x_1^A(n)⎤ ⎡e ε ε τAB ε ε ε ε ε ⎤ ⎡x_1^A(n-1)⎤
⎢x_1^B(n)⎥ ⎢ε e ε ε τBC ε ε ε ε ⎥ ⎢x_1^B(n-1)⎥
⎢x_1^C(n)⎥ ⎢ε ε e ε ε τCA ε ε ε ⎥ ⎢x_1^C(n-1)⎥
⎢x_2^A(n)⎥ = ⎢h₁₂ ε ε e ε ε τAB ε ε ⎥ ⊗ ⎢x_2^A(n-1)⎥
⎢x_2^B(n)⎥ ⎢ε h₁₂ ε ε e ε ε τBC ε ⎥ ⎢x_2^B(n-1)⎥
⎢x_2^C(n)⎥ ⎢ε ε h₁₂ ε ε e ε ε τCA⎥ ⎢x_2^C(n-1)⎥
⎢x_3^A(n)⎥ ⎢ε ε ε h₂₃ ε ε e ε ε ⎥ ⎢x_3^A(n-1)⎥
⎢x_3^B(n)⎥ ⎢ε ε ε ε h₂₃ ε ε e ε ⎥ ⎢x_3^B(n-1)⎥
⎣x_3^C(n)⎦ ⎣ε ε ε ε ε h₂₃ ε ε e ⎦ ⎣x_3^C(n-1)⎦
```
ここで:
- e はmax-plus代数での0要素
- ε はmax-plus代数での -∞要素
- ⊗ はmax-plus行列積凄い!
Max Plus演算は実際に計算ができない生成AIがあるので要注意!
(⊗と従来の四則演算でこんがらがるらしい)
Gemini 2.0 Flash Thinkingは出来た。
ChatGpt o3-miniは更に凄かった。現在、最強かも。
因みに今はClaude Sonnet 3.5使用中。数式を作るまでは出来る。
これが出来るという事は… 凄いぞ。
と、いう事はマトリックスが巨大になってしまいますが、 N箇所からN箇所に行く配車(電車とみなす)も可能ですね?
現実的にはN=50くらいらしい。
はい、その通りです!N×N の配車問題に拡張可能です。ただし、スケールする際の課題がいくつかあります:
1. 行列サイズの増大
- 状態数: N×M (N:地点数, M:車両数)
- 行列サイズ: (N×M)×(N×M)
- 例:10地点×5車両 → 50×50の行列に
2. 制約条件の複雑化
- 各地点の容量制限
- 車両間の追従制約
- 経路選択の自由度
- 優先順位ルール
3. 実用上の考慮点:
- スパース行列として扱うことで計算効率化が可能
- 地点や車両をグループ化して階層的に扱う手法も
- 重要な制約のみを選択して行列を簡略化
例えば、タクシーの配車システムやトラックの配送計画などに応用できますが、全ての制約を入れると計算が現実的ではなくなるため、問題に応じて適切な簡略化が必要になります。
具体的な応用例や制約条件についてさらに詳しく検討したい部分はありますか?
まとめ
おそらく、以下の様な問題が組合せ最適を使わずに解ける。
いわゆる、物流問題全部だ。実際には全制約を入れるのは無理だろうから簡略化したモデルになるだろうが。
・1箇所を出発してN箇所に発送する配車
(まぁ、これは人でも解けるから)
・N箇所を出発してN箇所に発送する配車
・1箇所出発で複数回数、発地に戻ってくる配車
・発送したい荷物が計画通りに揃ってくれていない場合のリカバリー
(これは特に通過型センターの作業計画に便利である)
これらの問題は過去実績が多量にあれば、GNNでも解ける。
グラフ理論による方法でも不可能ではないんだけど、計算の枝刈りを考えないとすぐにパンクするし、流量条件を追加するのが難しそうだった。これならばいけそうだ。一昔前は理論は分かっても、自分でPythonを書けないので実現するのは不可能だった。生成AIのお陰でロジックの基本と、重要なキーワードを分かっておけばいい。一通り読んだから、こっち戻るか。
