
AI 実装検定への道(4)
AI 実装検定 A級合格へ向けて学習を進めています。
前回投稿が3回目で、プログラミングの章を進めて書いています。Google Colaboratoryの利用は快適です。
前回は、シグモイド関数、Numpyを用いた配列の生成と、積の求め方。
さらには、配列を自動生成してくれるnp.zeros()、np.ones()、np.full()、np.arange、そして np.random。np.randomにおいては、np.random.random()、np.random.normal()、そしてnp.random.randintまで勉強してきました。その間に、データタイプに整数を表すdtype=int、浮動小数点を持った数値を表す、dtype=float。 データタイプを int にしてした場合、小数点以下が切り捨てになることを知ることができました。
今回は、前回の最後に出てきた np.random.randint が整数の配列により、画像データに活用されている・・・というあたりから再開します。
公式テキストでは、185ページの最後から。0〜9までの数字が、どのようにディスプレー上で表されているか?自身としては興味深い内容です。
スマホで撮影した写真が4,000ピクセル×3,000ピクセルで表されたとすると、これは4,000×3,000この数値を集めた配列に置き換えることができると解説されています。
このように考えると、コンピュータは高度に制御されたプログラムで動いていることが、少しばかり理解できる気がします。
NumPyの情報取得機能
手書き文字のデータセットで機械学習をする際によく用いられる「digits」を例として、配列の情報を取得していきます。
(コード記述)
import numpy as np
from sklearn import datasets
digits=datasets.load_digits()
これで、「digits」を呼び出したことになるのかな?
では、8の数字がどう表されているのか見ていきます。
(コード記述)
import matplotlib.pyplot as plt
plt.imshow(digits.images[8],cmap="Greys")
#plt.imshow(digits.images[8])
plt.show
(結果)
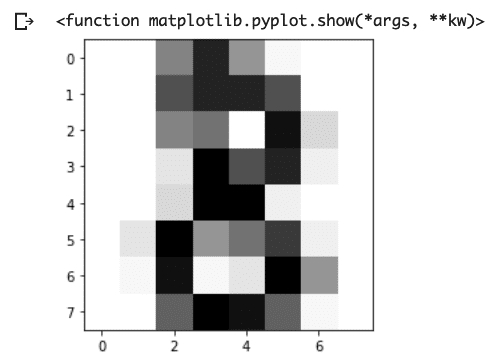
8×8のかなり荒いイメージセットなので、こんな感じですが、0〜9それぞれに見ていきましょう。
(コード記述)
import matplotlib.pyplot as pltplt.imshow(digits.images[0],cmap="Greys")
#plt.imshow(digits.images[0])
plt.show
(結果)
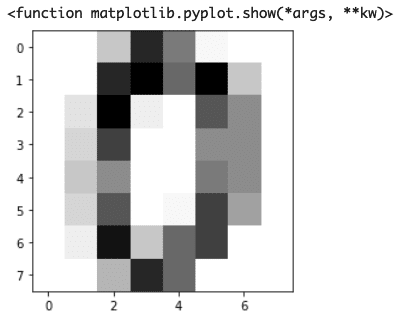
(コード記述)
import matplotlib.pyplot as pltplt.imshow(digits.images[1],cmap="Greys")
#plt.imshow(digits.images[1])
plt.show
(結果)
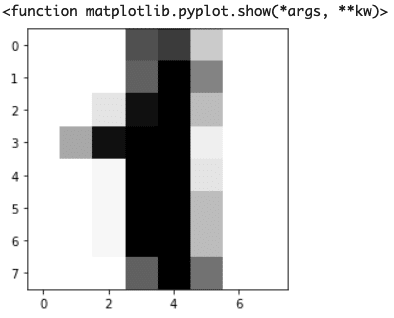
その他はこんな感じ・・・



これらを実際の配列に読み替えるのに、digits["images"]を実行します。
(コード記述)
digits["images"]
(結果)
array([[[ 0., 0., 5., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 15., 5., 0.],
[ 0., 3., 15., ..., 11., 8., 0.],
...,
[ 0., 4., 11., ..., 12., 7., 0.],
[ 0., 2., 14., ..., 12., 0., 0.],
[ 0., 0., 6., ..., 0., 0., 0.]],
これが、実際に0を表すときの行列です。
動作画面では、すべての数字の表示がされませんでしたが・・・実際にはこう表されているそうです。
[[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]]
各数値が色の濃淡を表していて、0〜16までの数値が入るそうです。
次の「target」の意味については、よく分かりませんでした・・・
(コード記述)
digits["target"]
(結果)
array([0, 1, 2, ..., 8, 9, 8])
(コード記述)
digits["images"].ndim
(結果)
3
(コード記述)
digits["target"].ndim
(結果)
1
(コード記述)
digits["images"].shape
(結果)
(1797, 8, 8)
以上のことから、「images」は8×8の配列の2次元データが何階層も重ねられることで3次元として表され、「target」はその数値そのものを特定する1次元であると解説されています。次に「shape」で導かれた結果についてを持った3次元の1797枚ある8欠けるの行列で示されるという意味らしい。
(コード記述)
x1=np.zeros(6,dtype=np.float16)
x2=np.zeros((3,4),dtype=np.uint8)
x3=np.zeros((2,4,5),dtype=np.float32)
「float16」とは、16ビットの小数点。
「unit8」とは、8ビット整数。
「float32」とは、32ビット小数点だとのこと
これを示したのちに、x1、x2、x3を見ていきます。
(コード記述)
x1
(結果)
array([0., 0., 0., 0., 0., 0.], dtype=float16)
np.zerosと示したので「0」を6つ並べた行列を示しました。
それぞれ小数点が置かれています。
(コード記述)
x2
(結果)
array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=uint8)
np.zeros((3,4))と示しましたので、3行4列の行列に0を配したものがアウトプットされています。各数値は整数です。
(コード記述)
x3
(結果)
array([[[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]],
[[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]]], dtype=float32)
np.zeros((2,4,5))と示していたので、4行5列の行列を2つアウトプットしています。それぞれ小数点がついています。次に、.ndimをつかて次元数を表します。それぞれ、1次元、2次元、3次元で表されるはずです。
(コード記述)
x1.ndim
(結果)
1
(コード記述)
x2.ndim
(結果)
2
(コード記述)
x3.ndim
(結果)
3
はいその通り、各1、2、3次元と表されました。
では、次に.shapeを使って形状を確認します。
それぞれ、1行6列で6、3行4列で3、4、そして2つの4行5列の行列を示すので2、4、5となるはずです。
(コード記述)
x1.shape
(結果)
(6,)
(コード記述)
x2.shape
(結果)
(3, 4)
(コード記述)
x3.shape
(結果)
(2, 4, 5)
はい、その通りの結果がアウトプットされました。
次は、.sizeを利用して、数値の個数を確認していきましょう。
最初は6、次は3×4=12、最後のは2×4×5=40となるはずです。
(コード記述)
x1.size
(結果)
6
(コード記述)
x2.size
(結果)
12
(コード記述)
x3.size
(結果)
40
この辺り若干退屈しますが、もう少し進んでいきましょう。
行列を抽出し、その構成(構造)を理解するには必要な工程なのでしょう。
NumPyによる配列の一部抽出と連結
NumPyを利用して、配列から一部の値を取り出せるということで、まずはrandamを利用して下記のように、0〜19までの20の数値からランダムに8つ数値を取り出してみます。
(コード記述)
import numpy as np
x1=np.random.randint(20,size=(8))
x1
(結果)
array([18, 7, 19, 10, 5, 14, 16, 11])
もちろんランダムに取り出すので、毎回実行すると結果は異なります。
もう一度実行すると・・・
(結果)
array([ 7, 11, 6, 8, 14, 18, 18, 3])
こんな風に結果が変わりました。
この中から、0番目から7番目まで選ばれた数値から、抽出してみます。
(コード記述)
x1[1]
(結果)
11
0、1、2、3、4、5、6、7番目までの8つの数値が並んでいるので、1を指定すると前から2番目の数値を選びます。この通り11が正解です。
(コード記述)
x1[3]
(結果)
8
こういうわけですね。
[ ]内にー(マイナス)を使うと後ろから何番目と指定できます。
(コード記述)
x1[-2]
(結果)
18
後ろから2番目なので、18で正解です。
(コード記述)
x1[-5]
(結果)
8
後ろから5番目。前から、0、1、2、3の順で4番目の数値ですね。
ある順位の番号に、新たな数値を代入することもできるそうです。
先ほどの後ろから5番目の数値8に12を代入してみます。
(コード記述)
x1[-5]=12
x1
(結果)
array([ 7, 11, 6, 12, 14, 18, 18, 3])
元の行列が array([ 7, 11, 6, 8, 14, 18, 18, 3]) だったので、後ろから5番目の8に12が代わりに置き換わったのが確認できます。
次は、同じようにrandomを利用して2次元の配列(行列)を生成します。
今度は、x1の代わりにx2を使用します。
(コード記述)
import numpy as np
x2=np.random.randint(20,size=(3,4))
x2
(結果)
array([[ 0, 2, 6, 1],
[ 4, 17, 7, 17],
[10, 4, 11, 1]])
これで、3行4列の配列(行列)が生成できました。
0 2 6 1
4 17 7 17
10 4 11 1
次にこの配列(行列)の数値構成をプログラムから問います。
(コード記述)
x2[0,0]
(結果)
0
配列(行列)の最初の数値を呼び出しています。
確かに0が位置しています。
[ ]内の数値は行、列の順で指定し、ここでも最初の配番は0からであり、
1行目を0、3行目は2で表します。
同様に2列目は1で、4列目は3で表されるので注意しましょう。
プログラムで書けばわかることですけどね。
では、2行目の3列目の数値7を呼び出してみましょう。
(コード記述)
x2[1,2]
(結果)
7
確かに7を返してくれています。
では、X1の時と同様に、どこかに別の数値を代入してみます。
ちょうど良いので、さきほどの7のところに3を入れてみます。
(コード記述)
x2[1,2]=3
x2
(結果)
array([[ 0, 2, 6, 1],
[ 4, 17, 3, 17],
[10, 4, 11, 1]])
良かった・・・意図した通りに変更できました。
もう少し続けます。
同様に、次はx3を用意して、今度は15までの数値で3×4の配列(行列)を生成してみます。
(コード記述)
x3=np.random.randint(15,size=(3,4))
x3
(結果)
array([[14, 0, 1, 0],
[ 5, 7, 5, 9],
[ 0, 8, 13, 11]])
今回は、少し長くなったのでここまでにします。
最後に、x1、x2、そしてx3を用意したので、次はここから続けていきます。
第4回のここでは、NumPyの情報取得機能を利用して、8×8の配列(行列)で示された0〜9までの手書き文字のデータセット(digit)を例として画像を読み込み、それぞれマス目の濃淡を0〜16で指定されて表されることを学び、その次に引き続きNumPyを利用して配列の一部抽出と連結を学び進めました。今回は途中までとなりましたが、「digits」「target」「images」「shape」「ndim」「size」を利用して、その配列(行列)に関する「target」「images」に対して「shape」=形状、「ndim」=次元数、「size」=含まれる数値の個数などをカウントしてきました。また、前回に引き続きrandamを利用してランダムに数値をピックアップし、1次元ないしは2次元の配列(行列)を生成し、x1、x2、そしてx3を用意するところまで進めてきました。中には、ある位置の数値を指定して置換するという「x2[1,2]=3」のような記述も含まれています。
ついつい、書きながら忘れてしまいがちですが、この一連のプログラムは「NumPy」を使って動かしています。勉強を再開するのに、今一度 import numpy as npの記述を追加するか、Google Colaboratory上の再開するプログラムの前回に戻って、 import numpy as npに記述のある部分を再実行してから進めていくといいでしょう。
今日のところはここまでです。
