
AI 実装検定への道(3)
AI 実装検定 A級合格へ向けて学習を進めています。
前回投稿が2回目で、プログラミングの章を進めて書いています。前回は「pandas」を使い、機械学習のライブラリ「sklearn」からdatasetsを使う方法を学び、花のアヤメのがく片と花びらの長さと幅の数値を表示すること、for 文、if 文、さらには関数を利用するところまで進めました。
今回は、なんだか難しそうですがシグモイド関数(sigmoid)なるものを見ていくことになります。公式テキストは173ページから始まります。
あ!忘れないうちに書いておこう〜
この公式テキストは、老眼者にはちときつい・・・「.」(ピリオド)か「,」(カンマ)か分かりにくい部分が多々ある。公式テキストを見ながら、キーボードで入力しつつ、ディスプレイで確認をしながら入力すると『エラー!!』・・・え!え!って戸惑って見返しても、どこが間違っているかすぐには分からない。メガネを外して、近視の裸眼でテキストに近づいて良く見ると「,」じゃん!ってなことがある。
私が入手したのは「初版第1刷発行」・・・出来れば、この公式テキストはA5版ではなくB5版に拡大して発行してほしいな〜
シグモイド関数(sigmoid)
まず、このサイトをのぞいてみよう。
シグモイド関数とは?ニューラルネットワークで用いられる理由についても解説
”シグモイド関数は、ニューラルネットワークの活性化関数でよく用いられています。しかし、なぜシグモイド関数を用いるのか、どのような利点があるのか?”
シグモイド関数はネイピア数eを用いた次の数式およびグラフで表されます。f(x)=1/(1+e⁻ᵃˣ) (a>0)と書かれています。
公式テキストでは、ςₐ(x)=1/(1+e⁻ᵃˣ)と書かれていますが気にしないでもいいですよね?
”シグモイド関数は微分形を求める計算が容易であるため、NNの逆誤差伝搬法(バックプロパゲ―ション)に活用できることがメリットです。逆誤差伝搬法とは、モデルの理想的な出力と実際の出力との誤差を入力側の層に伝えることで、モデルのパラメータを決定するアルゴリズム。層数の多いNNで用いられる代表的な計算手法です。”と解説されています。
公式テキストに戻ります。
(コード記述)
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.linspace(-10,10)
y=sigmoid(x)
plt.plot(x,y)
plt.show()
これを実行すると、下記のグラフが生成されます。
(結果)
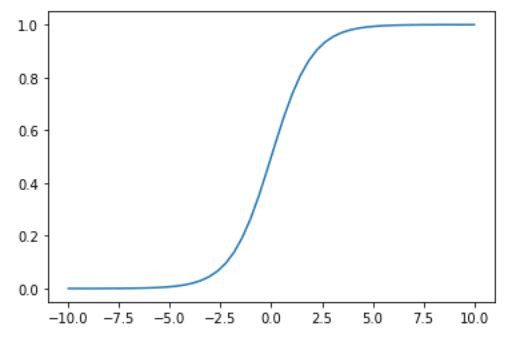
シグモイド関数を微分した時のグラフ(微分積分はあまり好きではなかったので、この辺あまりよく分かっていないですが・・・)
(コード記述)
dydx=(1-sigmoid(x))*sigmoid(x)
plt.plot(x,dydx)
plt.show()
(結果)
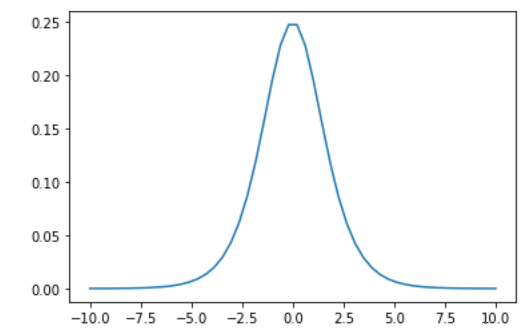
公式テキストでは、微分した時の最大値が 0.25 (x=0) と解説されているので、その通りになっていることが分かりました。
シグモイド関数と、それを微分したグラフを重ねて表示することもできるみたいです。
(コード記述)
plt.plot(x,y)
plt.plot(x,dydx)
plt.show()
(結果)
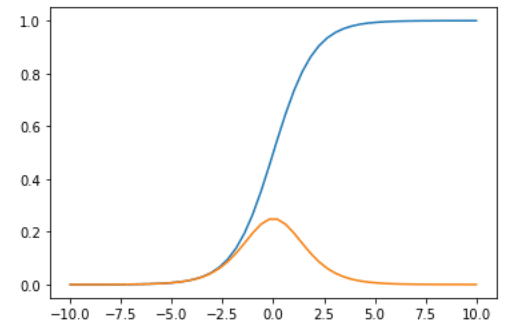
私の環境は、MacでGoogle Colaboratory を利用しているため、Windows他の環境では、表示のされ方が異なるかもしれません。(念のため)
NumPyの利用
Pythonは、比較的プログラミングが容易で使いやすいそうですが(初めての私にはどうだか・・・)、C言語やC++言語と比較すると処理速度がやや遅いそうです。そのために、配列(行列)の計算をより高速に行えるようにNumPyが用意されているとのこと。このNumPyの中身はC言語やC++言語で作られていると解説されています。
すでに第1回目でも勉強しましたが、NumPyをプログラム上で使えるようにするためには、最初にインポートする必要があるため、import numpy as np
と最初に記述する必要があります。
NumPyを用いて下記の3行3列の行列を生成しなさい。
(以下は、公式テキストと数字を変えて実施しています)
3 5 7
2 6 9
1 4 8
(ここでは、行列を示す大括弧は省略します)
(コード記述)
import numpy as np
np.array([[3,5,7],[2,6,9],[1,4,8]])
(結果)
array([[3, 5, 7],
[2, 6, 9],
[1, 4, 8]])
NumPyを用いて、下記の3行1列の行列を生成しなさい。
2
7
9
(ここでは、行列を示す大括弧は省略します)
(コード記述)
import numpy as np
np.array([[2],[7],[9]])
(結果)
array([[2],
[7],
[9]])
NumPyを用いた行列の計算
行列の計算なんてどうするものか、全く忘れていました。
下記サイトの解説を読んでみます。
行列の積(掛け算)とは何か?わかりやすく解説
なんだか私には分かりにくい解説ですが・・・こちらを引用します。
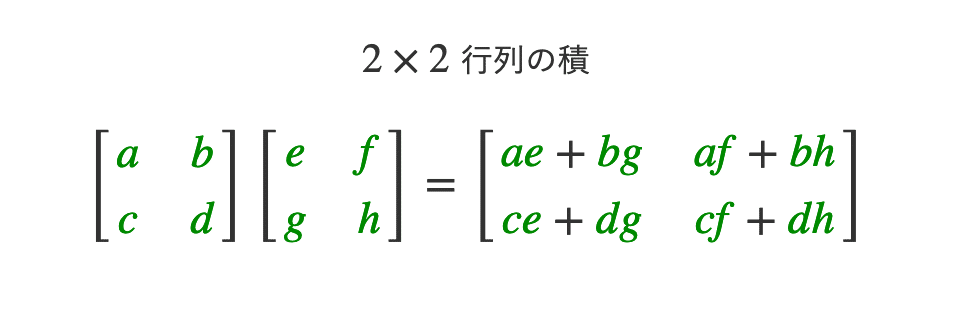
2×2行列の席を求める場合、
左の行列における上段と、右の行列の1列目を順に掛けて和を求める。
次に、左の行列における下段と、右の行列の1列目を順に掛けて和を求める。左の行列における上段と、右の行列の2列目を順に掛けて和を求める。
さらに、左の行列における下段と、右の行列の2列目を順に掛けて和を求める。・・・というふうにするそうです。
NumPyをもちいて、次の行列の積を求めなさい。
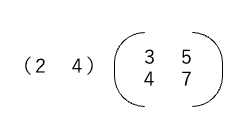
まずは、手元で計算してみます。
2×3+4×4=22 2×5+4×7=38
計算結果は、1行2列の行列となるはず・・・左の行列をxとして、右の行列をyとします・・・
(コード記述)
import numpy as np
x=np.array([2,4])
w=np.array([[3,5],[4,7]])
x.dot(w)
(結果)
array([22, 38])
良かったです。手元計算が合っていたので、行列の計算に少し離れてきたかもしれません。AとBの行列の積は、A.dot(B)あるいは、A@(B)と表すことができるそうです。念のため、A@Bとしてみます。
(コード記述)
import numpy as np
x=np.array([2,4])
w=np.array([[3,5],[4,7]])
x@(w)
(結果)
array([22, 38])
上と同じ結果を得られました。
もう少し行列の計算に離れておいた方が良さそうなので、先に引用した2×2行列の積を試してみましょう。下記の場合はどうなるでしょうか?
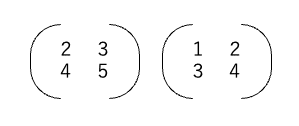
まずは手元で計算してみます。
2×1+3×3=11 2×2+3×4=16
4×1+5×3=19 4×2+5×4=28
11 16
19 28
こんな風になるでしょうか?
(コード記述)
import numpy as np
x=np.array([[2,3],[4,5]])
w=np.array([[1,2],[3,4]])
x@(w)
(結果)
array([[11, 16],
[19, 28]])
良かった、その通りの結果を得られました。ここでは、2×2行列の積までしかやりませんが、これが10×10行列とかなるとなかなか手ではできませんね。こうして、NumPyを使えるようになれば容易なことは分かりました。次に進んでいきます。
NumPyで配列の自動生成
np.zeros() を利用すると、括弧内に指定した数だけ0で埋めた配列(行列)を生成してくれるそうです。
(コード記述)
import numpy as np
np.zeros(6)
(結果)
array([0., 0., 0., 0., 0., 0.])
このままでは、小数点を保持していますので、データタイプを整数とします。その場合、dtype=int と記述します。dtype:勝手にデータタイプと覚えた。int:英語で整数を表すintegerから来ているそうです。
(コード記述)
import numpy as np
np.zeros(6,dtype=int)
(結果)
array([0, 0, 0, 0, 0, 0])
np.zeros() には、行だけでなく列を指定することも出来るそうです。
np.zeros((行数,列数))というように。ここで、括弧が二重になっていることに注意しなければなりませんね。
(コード記述)
import numpy as np
np.zeros((6,3))
(結果)
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
念のため正数に揃えておきましょう。
(コード記述)
import numpy as np
np.zeros((6,3),dtype=int)
(結果)
array([[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
果たして、これがなんの役に立つのかわからなくなてきましたが、次に進んでいきます。次は、np.zeros()に代わり、np.ones()・・・zeroでなくoneなので行列を1で埋める役割です。ちょっと大きめに5×6の行列を作ってみます。(整数にしておきましょう)
(コード記述)
import numpy as np
np.ones((5,6),dtype=int)
(結果)
array([[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]])
公式テキストでは、浮動小数点を表す float が解説されています。解説のように、整数指定してしまうと割り算をした時に小数点以下は切り捨てられてしまうため、不都合があります。そうなら、dtype=int を使わないで整数指定しなければいいじゃないかと思うんですが、一応解説に従います。
(コード記述)
import numpy as np
np.ones((5,6),dtype=float)
(結果)
array([[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]])
次は、np.zeros()、np.ones()に続いて、np.full()だそうです。0、1ではない指定の数値で行列を埋めてくれます。
(コード記述)
import numpy as np
np.full((5,6),2684)
(結果)
array([[2684, 2684, 2684, 2684, 2684, 2684],
[2684, 2684, 2684, 2684, 2684, 2684],
[2684, 2684, 2684, 2684, 2684, 2684],
[2684, 2684, 2684, 2684, 2684, 2684],
[2684, 2684, 2684, 2684, 2684, 2684]])
2684に変えて、3.14にしてみます。また、整数指定してみると・・・
(コード記述)
import numpy as np
np.full((5,6),3.64,dtype=int)
(結果)
array([[3, 3, 3, 3],
[3, 3, 3, 3],
[3, 3, 3, 3]])
あ!確かに整数指定すると『切り捨て』になっていることが分かりました。
そのうち、四捨五入する書き方とか教えてくれると思います。
次は、np.zeros()、np.ones()、np.full()に続いて、np.arange。
(初期数値,最後の数値,移動幅?)の順に数値を示し1次元の行列を生成するようです。やってみましょう。
(コード記述)
import numpy as np
np.arange(2,30,3)
2〜30までにおいて、3つ飛ばしに行列を埋めるとイメージしました。
ありゃ?アレンジの意味かと思って、arrangeとしたら大間違い。r をダブらさないで arange とするのが正解です。
(結果)
array([ 2, 5, 8, 11, 14, 17, 20, 23, 26, 29])
次は、np.linspace。arangeと同様に括弧内で要素を示すのですが、最後の三つ目は等間隔を指定します。(初期数値,最後の数値,等間隔)
こんな感じです。
(コード記述)
import numpy as np
np.linspace(2,30,8)
(結果)
array([ 2., 6., 10., 14., 18., 22., 26., 30.])
これ、うまい具合に等間隔になったので、間隔を9にして意地悪しちゃいます。
(コード記述)
import numpy as np
np.linspace(2,30,9)
(結果)
array([ 2. , 5.5, 9. , 12.5, 16. , 19.5, 23. , 26.5, 30. ])
間隔を9にしても、意外にうまく収まりました。
間隔を10にしてみると・・・
(コード記述)
import numpy as np
np.linspace(2,30,10)
(結果)
array([ 2. , 5.11111111, 8.22222222, 11.33333333, 14.44444444, 17.55555556, 20.66666667, 23.77777778, 26.88888889, 30. ])
あらら、なかなか難しい数字になりましたね。
このlinspaceは、グラフを描画する際にmatplotlibで活躍するようです。確かに、数値の間をうまく等間隔で示してやれば、グラフに利用出来そうです。次は、randomを利用します。前回には、サイコロの目をランダムに返すということで試みたものです。まずは、0〜1の範囲でランダムに4×3の行列を生成してみます。
(コード記述)
import numpy as np
np.random.random((4,3))
(結果)
array([[0.7249841 , 0.12158036, 0.48914526],
[0.6427853 , 0.28536344, 0.87184283],
[0.23164241, 0.36374326, 0.51025574],
[0.4539188 , 0.29251418, 0.94394591]])
また難しいワードが出てきました。『正規分布』に基づいた配列を生成するrandom.normal やてみましょう。0を平均値として分散値を1とします。即ち、−1〜1の範囲で、指定の行列を生成するというもの。
(コード記述)
import numpy as np
np.random.normal(0,1,(3,4))
(結果)
array([[ 0.6352216 , -0.59419916, 0.80137606, 0.14850093],
[-1.29893048, 0.92624618, 0.76831096, -0.13979871],
[ 0.80426805, -0.77073353, 1.36826564, 0.87526533]])
最後に、もう一つ。randint についても勉強します。
同じく、randomに数値を配列に収めてくれるもの。指定範囲を先に示し、配列を指定することで動きます。
(コード記述)
import numpy as np
np.random.randint(2,30,(4,5))
(結果)
array([[ 4, 20, 26, 23, 18],
[24, 26, 21, 5, 7],
[10, 17, 29, 16, 14],
[ 5, 26, 26, 16, 6]])
今回は、シグモイド関数、Numpyを用いた配列の生成と、積の求め方。さらには、配列を自動生成してくれるnp.zeros()、np.ones()、np.full()、np.arange、そしてnp.random。np.randomにおいては、np.random.random()、np.random.normal()、そしてnp.random.randintまで勉強してきました。その間に、データタイプに整数を表すdtype=int、浮動小数点を持った数値を表す、dtype=float。 データタイプを int にしてした場合、小数点以下が切り捨てになることを知ることができました。
次回は、今回の最後に出てきた np.random.randint が整数の配列により、画像データに活用されている・・・というあたりから再開していきます。
今日のところはここまで
