
統計学を知らざるを得ない話し #1
水色のパンツを履いた色黒の女の子の確率
仮に2000人の女の子を集めたとします。その中に何人、水色のパンツを履いていて、かつ色黒という女の子がいるでしょうか?
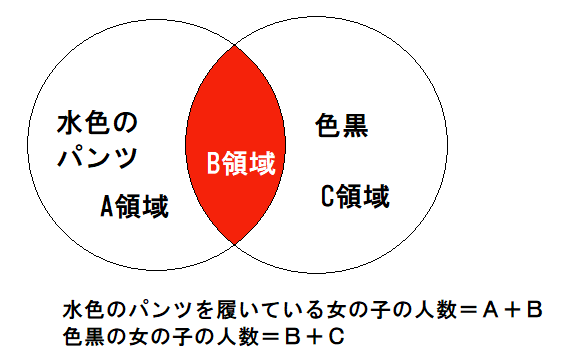
B領域の人数が答えです。もしかすると、水色パンツ率(水色のパンツを履いている確率)と色黒率(色黒である確率)を掛け算することでも目安として算出できるのではないかと思ったかもしれません。たとえば水色パンツ率が16%で、色黒率が5%であれば、0.8%の確率だろうと、、、しかしそれは独立事象だった場合です。色黒の女の子だろうと色白の女の子だろうと、同様に確からしく水色のパンツを履き得る場合の推定量になります。

独立事象かどうかを確かめる方法はたくさんありますが、文脈を変えて、「色黒の女の子が水色のパンツを履きやすいかどうかを確かめる」というのであれば分割表とカイ二乗検定は有効なツールの一つになります。

上述のようなデータが確認できれば、独立事象だという主張にはもっとも都合のよいデータをとることができたと言えます。しかし、

上述のデータは一見、先ほどのものと誤差の範囲に見えるかもしれませんが、統計学(自由度1のカイ二乗検定)は「色黒の女子が似合うと思って狙って水色のパンツを履いている可能性」を指摘せざるを得ません。
