
「亜両面は弱い」というのはつまりどういうことなのか
はじめに
また麻雀の話です。
今回は4連形、中ぶくれ、亜両面について考えました。とは言っても、個人的にはだいぶ長い間この問題を考え続けてます。
当記事も10年前に天鳳のSNSというサイトに上げた記事(「覚書 連続形同士の比較について」)のリライトです。
リライトと言っても中身はほとんど別のものになり、自説も修正しました。
元の記事は末尾に貼っておきます。
用語の定義
まず用語と基本的なことを説明します。
・4連形、中ぶくれ、亜両面
例えば456mに3m(7m)、4m(6m)、5m、をそれぞれ1枚足した形を考えます。
すると
3456m(4567m)
4456m(5677m)
4556m
の3種類の形が得られます。
これらは上から順に4連形、亜両面、中ぶくれと呼ばれています。
また、これら4枚からなる形をここでは4枚形と呼んでおきます。
・4枚形の共通点と相違点
この4枚形の共通点は、メンツ+孤立牌として見ればくっつき形(例 3345m→3m+345m)に取れる点です。
4連形だけメンツを2種類に取れます(例 3456m→345m+6m、3m+456m)。
4枚形のくっつき形は、メンツ+ただの孤立牌(例 345m+6p)よりも強い形です。なぜならターツ×2にもとれるからです。
そのターツ×2が、両面ターツ×2なのか両面ターツ+トイツなのかという違いがあります。
・端、端の一個隣、真ん中
またこの4枚形には、
端(1234、1223、1123)
端の一個隣(2345、2334、2234)
真ん中(3456、3445、3345)
の三つのレベルがあり、それぞれ微妙に形が違います。例えば、同じ4連形でも端に行くほど機能は落ちます。
結論
先に結論を述べます。
4枚形の3種類の形の基本的な関係は、打点を除けば、
4連形が一番強く(端を除く)、
①ヘッドがあるときは亜両面が弱くなり、
②ヘッドがないときは中ぶくれが弱くなる。
ただし、ルール①と②が重複する場合、②のヘッドレスの中ぶくれ形を嫌うべきである。
(ヘッド候補が両面トイツ形で、亜両面と中ぶくれとの比較になる場合、牌理の原則はくっつき形>ヘッドレス形なので)。
結論はこれです。
まずはヘッドの確定している形から考えます。
ヘッド確定形
⑴単独トイツ形

まずはヘッドが決まっている形です。
結論はとてもシンプルで、1sというヘッドがあるので亜両面が一番弱くなります。ゆえに打6sです。

⑵ヘッドレス形

対して、メンツから独立したトイツがない形を考えてみます。独立したヘッドがないのが確定している形と言い換えても良いかもしれません。
この形は先程とは逆に、中ぶくれと両面ターツの相性が良くありません。
中ぶくれ形はヘッド+両面ターツや、良形6枚待ちに受けられないからです。
ターツはもう足りてて、あとは頭をどこで作るかという話になると、中ぶくれは途端に弱くなります。
この形は打6pです。

その点で4連形は有能です。両面ターツ×2に分解できるし、最終形になっても悪形にはなりません(6枚待ちという点なら亜両面と同等です)。
繰り返しますが、結論は、
ヘッドがある場合、亜両面が弱くなる。
ヘッドがない場合、中ぶくれが弱くなる。
こうだと思います。
ヘッド不確定形
では、ヘッド候補がトイツにも両面ターツにも変化できるような、両面トイツ形の場合はどうなるでしょうか。これが次の問題です。
なぜ「両面」トイツなのかというと、悪形の複合トイツ(カンチャントイツとペンチャントイツ)の場合、トイツ固定して話はおしまいだからです。
4枚形のいずれかをメンツとして固定し、単独ヘッドに浮いた1枚をくっつけて両面トイツにします。
両面トイツ+4枚形×2(+1メンツ)
この両面トイツにプラスされる4枚形×2の組み合わせを比較していきます。
その際に先程の結論を以下のように言い換えます。
・亜両面+トイツ
・中ぶくれ+両面ターツ(両面トイツ)
この2つのペアを避けること
言い換えたのは、こちらの方が牌姿のチェックが容易になるからです。
なお、この2つの原則がぶつかったとき、より避けなければならないのは中ぶくれ+両面ターツ(両面トイツ)のペアの方です。
両面トイツをトイツ固定して亜両面+トイツの形にするのは、4メンツ1ヘッドの条件をクリアしているため、くっつき形です。
対して、両面トイツを両面固定して中ぶくれ+両面ターツの形にするとヘッドレス形になってしまいます。
ヘッドとターツの作りやすさの比較だとヘッドを作る方が大変なので、一般的な1シャンテン形の優劣はくっつき形>ヘッドレス形となります。
なのでどちらか選ぶとなったら、より避けるべきは中ぶくれ+両面ターツの形(ヘッドレス形)なのだと思います。
⑴両面トイツ形
・4連形+4連形

→4枚形最強の4連形×2という最強コンビです。
形としては3sを切るか、4連形の端を嫌うかの二択です。
打3sは、4連形×2+ヘッド
打36m47pは、4連形+両面トイツ
です。この形はちょっと厄介で、いくつかのシュミレーターによると全てトイツ固定(打3s)有利に出ます。
しかし、両面トイツをトイツに悪形固定するのは感覚として非常に気持ち悪く、美しくありません。
現麻もどちらかの4連形を切るべきとなっています。
ただ、気持ちが悪いと言うような理由だけならそのうち書き換わるかもしれないとも思ってます。
ちなみに打4sのような、唯一のヘッドを壊してヘッドレスに受ける形は、打点のない手では悪手になることが多いです。
あくまでくっつき形>ヘッドレス形が基本だからです。

・4連形+亜両面

→4連形>亜両面なので亜両面切りの打4mで良いと思います。
打3sだと、亜両面+トイツの禁忌に触れてしまいます。打4sもヘッドレス形なので悪手です。

・4連形+中ぶくれ

→中ぶくれ+両面ターツ(両面トイツ)の禁忌を拒否するには、
・打5m 中ぶくれ自体を消すか
・打3s トイツ固定で両面ターツ(両面トイツ)を消すか
の二択です。
私はこれまで打5mを正着だと信じてきましたが、打3sの方も一盃口の打点が強いみたいで微差です。
微妙な違いで結論は変わるとも思いますが、いずれにしても禁忌を避けられているならそれで良いと考えています。

・亜両面+亜両面

→これはどちらかの亜両面を嫌うのが良いです。打3sもくっつき形ですが禁忌込み、打4sがヘッドレス形なのはすでに述べました。

・亜両面+中ぶくれ

→この形はよく見かけますが、
打3sは亜両面+トイツ
打4sは中ぶくれ+両面ターツ
打6pは中ぶくれ+両面トイツ
でいずれも禁忌なので、それらを避けると打5mが残ります。
ただ、打3sはかなり有力で形によってはこちらが正着になることも多いように思います。打6pも成立の余地はあるみたいです。
とりあえずの亜両面切りや両面固定が通じない非常に面白い形です。

※記事の末尾に追記あり
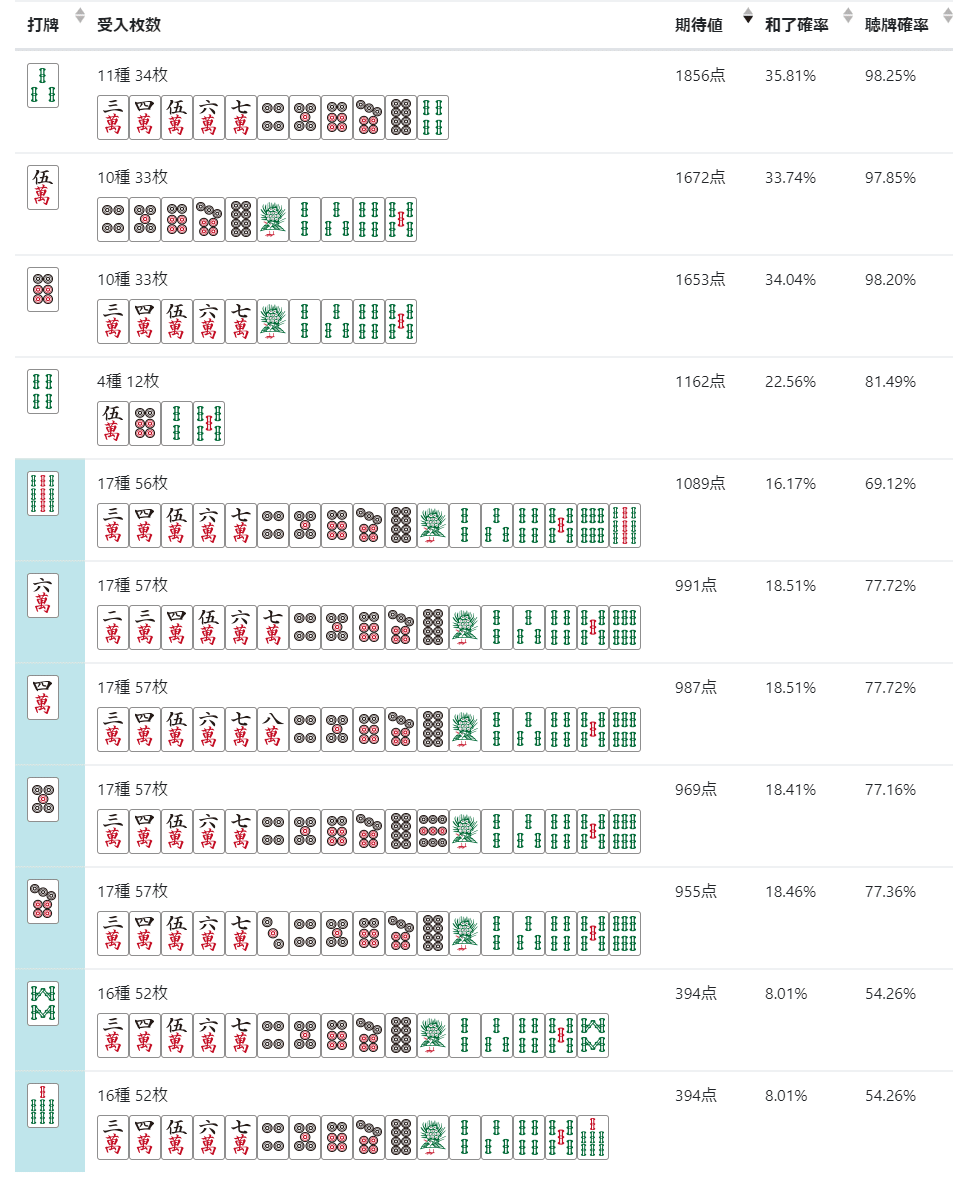
・中ぶくれ+中ぶくれ

→これは打3sで中ぶくれ+両面ターツの禁忌を拒否できます。
8枚ウイングをヘッド固定するのもこの手筋の一種だと思います。
⑵複合トイツと複合形
ここでは4枚形にさらに何枚かプラスされた形をとりあえずは「複合形」としておきます。
複合形の方が単純な形よりもヘッドもメンツも作りやすいのは分かると思います。
そのため、ヘッドがあるのと同じような効果が得られることから亜両面が弱くなりそうですが、話はそう単純でもありません。
そもそも常に複合形残しで良いかというとそうでもない気がします。
この問題はもう少しつついてみたいので保留にしておいて、以下では、複合形の中では単純な三面トイツについてのみ考えてみます。
〇三面トイツ形
両面トイツの両面部分が三面張になった形を三面トイツと呼ぶことにします。次にこれを考えてみます。
・三面トイツ+亜両面+中ぶくれ

→三面トイツがあるため、三面トイツ(複合形)>中ぶくれ>亜両面で打5pになりそうですが、最終形重視で打6sが良いようです。
677m部分と中ぶくれのペアが禁忌で、強い方(複合形)残しということなんですかね。

・三面トイツ+中ぶくれ+中ぶくれ

→中ぶくれ×2は、単純形ではヘッド固定でした。
しかし、三面トイツとなるとシミュレーターで打36m4p6sにはほとんど差がありません。
複合形という強い部分をヘッドに固定してしまう損と、中ぶくれ+677mの禁忌が拮抗しているんですかね。

・中ぶくれ三面トイツ+亜両面+中ぶくれ

→三面トイツのトイツ部分が一つ内側に寄った形です。これを中ぶくれ三面と呼んでおきます。
これも打6sのようです。667mと中ぶくれが禁忌で、強い方(複合形の667m)残しということですかね。

・中ぶくれ三面トイツ+中ぶくれ+中ぶくれ

→中ぶくれが親の敵のように集まった、中ぶくれ祭りみたいな牌姿ですが、流石に複合形が強いと言ってもこれはヘッド固定の打7mになるようです。
中ぶくれ界隈でもそっちのほうが筋が通ると思います。

打点での例外
4枚形の基本的な関係は、「打点を除けば」という留保が付いていました。
4枚形の3種類の形の基本的な関係は、打点を除けば、
4連形が一番強く、・・・(以下略)
優劣と言っても微差なので、打点差があると期待値が逆転しやすいからです。
三色やドラ、タンヤオなどで打点差が出る場合、ヘッドレスに受ける手筋が出てくることがあります。

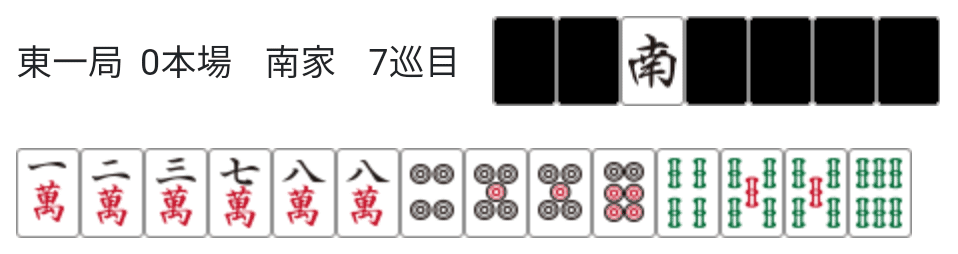
例えばこの手は形だけだと、
①くっつき>ヘッドレス
②ピンズ複合形>マンズ4連形
で、4m(1m)を切る形ですが、123と234の三色があり三色を追う方が期待値が高くなります。正着は123と234の双方を追う打2sです。
ヘッドレス形に受ける打2sは、良形は確定しますが、くっつき形に比べて受け入れが減るので通常は悪手になります。
ただ、このくらい打点差があるときには成立することがあります。

演習問題







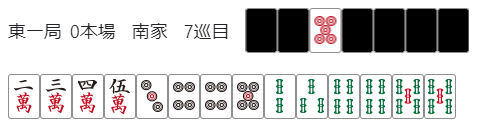
発展問題
自作の微妙なのを載せておきます。解答はありません。









亜両面が弱いとはどういうことか
4枚形比較何切るで見落とされた点

これは当記事で一番最初に出した牌姿です。
この牌姿は私が考えたものなのですが、見たことのある方もいるかもしれません。現麻に採用されているからです(p68の牌9)。


この日記を書くだいぶ前から4枚形の優劣については知識として持っていました。
どこのサイトで見たのかは忘れましたが、昔から知られている結論なのでしょう。
※追記 2024.10.10

ある時、4枚形の3つの形にヘッドを足した14枚形を何切るにすれば三者の形の優劣を一望のもとに示せるのではないかというアイデアが閃きました。
そこで早速、三色を消し、タンヤオを消し、純粋に形だけで期待値が比較できるように牌姿を調整してコミュニティの日記に投下しました。
この問題は、簡単に言うと6m6p6sのうちどの6を切るのが良いですかと問うものです。
ただ、当時はあまり自覚していませんでしたが、この形には暗黙の前提がありました。
それはヘッドが確定しているという点です。
ヘッドがすでにある以上、強いくっつき形に受けられる形には、これ以上のヘッドは不要です。
その結果、4枚形のうち両面ターツ×2に分解できない亜両面が弱くなるのは当たり前なのです。
わかってしまえば「なんだ」という感じですが、私はそこをあまり深く考えませんでした。
10年前の認識について
自戒を込めて過去の自分の発言を拾ってみました。
メモ:中膨れと亜両面とノベタンの比較。原則は中膨れ>亜両面。ただし、頭となりうる塔子がない場合、亜両面を残した方がスムーズ。特徴は、中膨れは良形ができやすいが最終形が弱く、亜両面はその逆。ノベタン(4連形)はその中間。良形受け入れ的に中膨れであり、最終形としては6枚受けが可能
— まだちぃ。 (@madarasensei) July 25, 2012
@mjharu 亜両面は枚数が弱く最終形が強い。中膨れは良形率が高いけど最終形が弱い。ノベタンは水陸両用(良形枚数は中膨れと変わらず、最終形が亜両面と同じ)。なので原則はノ>中>亜だけど、頭が連続系の場合渡れるので、亜両面のフォローが利く分中膨れを切る場合があるってなったんだけど
— まだちぃ。 (@madarasensei) September 21, 2012
@gomu_toituba 大雑把に言うと、4連形があればそれ残し、逆に亜両面は大体切ってOK、中膨れと亜両面比較も原則中膨れ残しという認識で牌理上は8割OK。残りの2割は両面対子(223pみたいな形)+中膨れ+亜両面みたいなコンボは例外的に亜両面が強いって覚えとけばいいかと思う
— まだちぃ。 (@madarasensei) June 6, 2015
この頃はリプライ飛ばしまくってたので、他にも検索すれば沢山ひっかかるのですが、内容はほぼ変わらないのでこれくらいにしておきます。
要は「原則は亜両面切りで、例外的に両面トイツ+亜両面+中ぶくれになったときは最終形を重視して中ぶくれを切るべき」という認識です。
自分でもこのルールを発見したときはそれなりに自信があったのですが、現在から見ると、自分の作った例(3456m5667p116678s)に引っ張られているし、結論も十分ではなかったと思います。
どこが十分でないのかというと、上の説明では、なぜ例外は例外なのか、例外は全部でいくつあってそれで全部なのかを説明できていないと思うからです。
また、例外にあてはまるべき形なのに、シュミレーター等にかけてもあてはまらない牌姿を単に打点で片付けていたこともありました。
中ぶくれを残せば一盃口分だけ打点期待値が増えるのは当たり前で、そこも説明になってなかったように思います。
なぜ両面トイツ+亜両面+中ぶくれは例外か
そもそもなぜこの形が例外かというと、
ヘッドの候補が両面トイツという、トイツにもターツにもとれる中間のときに、ヘッドがある場合の原則(亜両面+トイツを避ける)と、ヘッドがない場合の原則(中ぶくれ+両面ターツを避ける)が衝突するから
だと思います。
そこに例外の例外たる所以があるのだと思います。
再度確認しておくと、この問題の核心は本文で述べましたが、
ヘッドがあるかないかで4枚形の評価が変わる点
です。
なので、中ぶくれより亜両面が弱いかは、手牌にトイツがあるかに拠ります。
では、そのトイツが両面トイツで、トイツとターツどっちつかずで亜両面と中ぶくれの選択が生じたらどうすればよいのか。
そのときはより強い禁忌である中ぶくれ+両面ターツを避けたくっつき形に受ければよいということでした。
他にも例外はあるのか
では、例外は他にもあるのでしょうか。
4連形の比較をヘッドという観点から行う場合、ヘッドの存在がはっきりしている場合、取りうる選択肢はヘッドが「あるかないか」の二択です。第三の選択肢はここにはありません。
比較の観点は他にもあると思いますが(打点、端etc)、ヘッドという観点から「あるかないか」と問うた場合、それ以外の選択肢はないのです。
ゆえにヘッドがはっきりしている場合、話はそれで尽きています。
では、ヘッドがはっきりしていない場合、言い換えれば、ヘッド候補のトイツがターツにもなりうる形のような場合(両面トイツの場合)はどうでしょうか。
この場合に取りうる選択肢は「両面トイツをトイツ(ヘッド)に取るか、ターツに取るか、両面トイツには触らないか」の三択です。
前の2つが「両面トイツに触る」で、後ろの「両面トイツに触らない」と対を成しています。この観点にも中間はありません。
詳細は本文で述べたつもりですが、中ぶくれと両面ターツ(両面トイツ)の組み合わせを禁忌とすることを中心に、上に挙げた分岐は一応全て説明はできたのではないかと思います。
なので、原則同士がぶつかり合うケース(例外)はこれ以外にはなく、この問題は原理的に説明できたのではないかと思います。
まとめると、「亜両面が弱い」というのは、あくまでもヘッドが確定しているケースでの説明でしかないと私は理解しています。
4枚形を比較する全てのケースを集めたとき、亜両面を嫌うべき牌姿が全体の何割を占めるのか私にはわかりません。
4連形よりは亜両面を切る機会が増えると思われるので、あるいは多少は多いのかもしれません。
ただし、「単に亜両面を嫌え」と言っているだけでは原理的な理解からはほど遠いと思い、今回この記事で一石を投じてみた次第です。
おわりに
4連形、中ぶくれ、亜両面という分類は10年前よりはだいぶ広まったと思います。
ただ、三者の関係を体系的に位置づけて、原則と例外を説明しているものを見たことがあまりありません。
私自身「亜両面を切れ、切れ」というばかりで、その例外がなぜ例外なのかを明確に自覚できていなかったように思います。
ただ、最初の結論にもそれなりに愛着はあるので、自戒を込めて、認識の一里塚としてここに供養しておきます。
当記事で牌理関係は3作目ですが、過去2作(1シャンテンピーク理論とスリーヘッド最弱理論、両翼形とウイング形)のいずれも雀頭が重要な位置を占めています。
雀頭というルールを付け加えた人は天才だと思います。
演習問題解答
問1


問2


問3


問4


問5


問6


問7

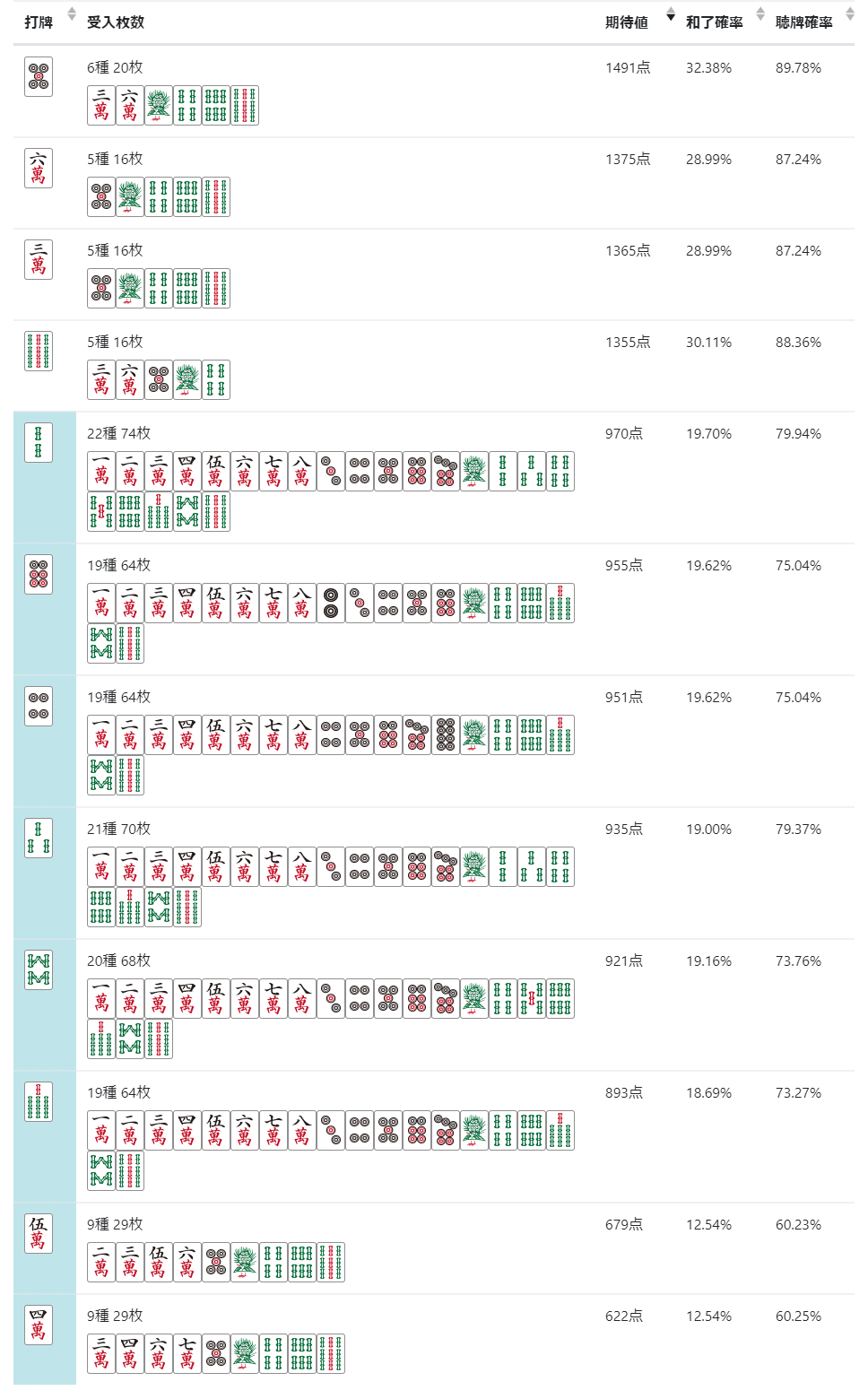
問8


発展問題の評価値
発展1


発展2


発展3


発展4
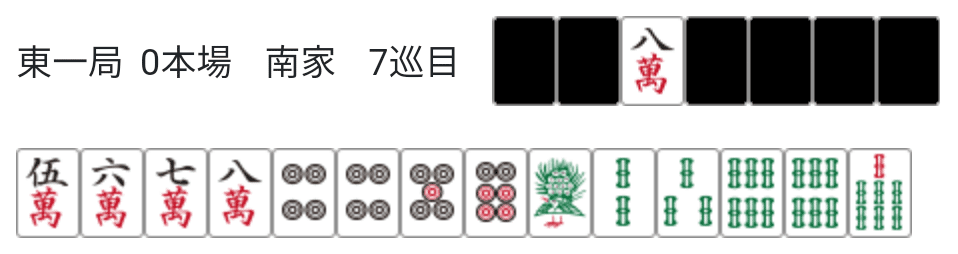

発展5

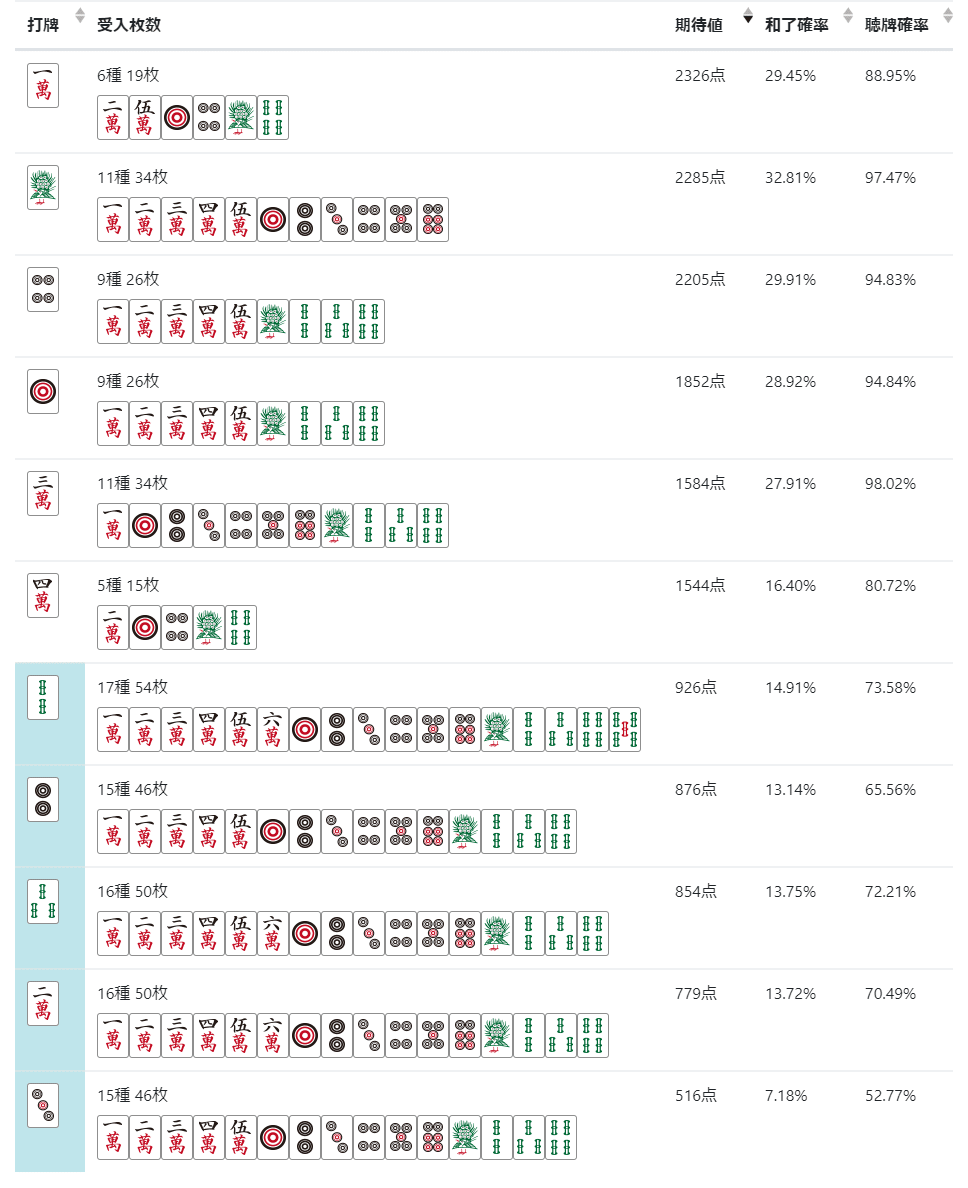
発展6


発展7


発展8


発展9


発展10

追記 ヒロポンさんからの異論
両面トイツ+亜両面+中ぶくれの形について、ヒロポンさんから異論が出されたので追記します。
当記事でのこの形の結論は、
禁忌を拒否しうる中ぶくれの解消を第一に挙げ、トイツ固定も有力、亜両面切りが成り立つ場合もある
としました。
これに対して次のような問題が出されました。
ヒロポンさんからの疑問

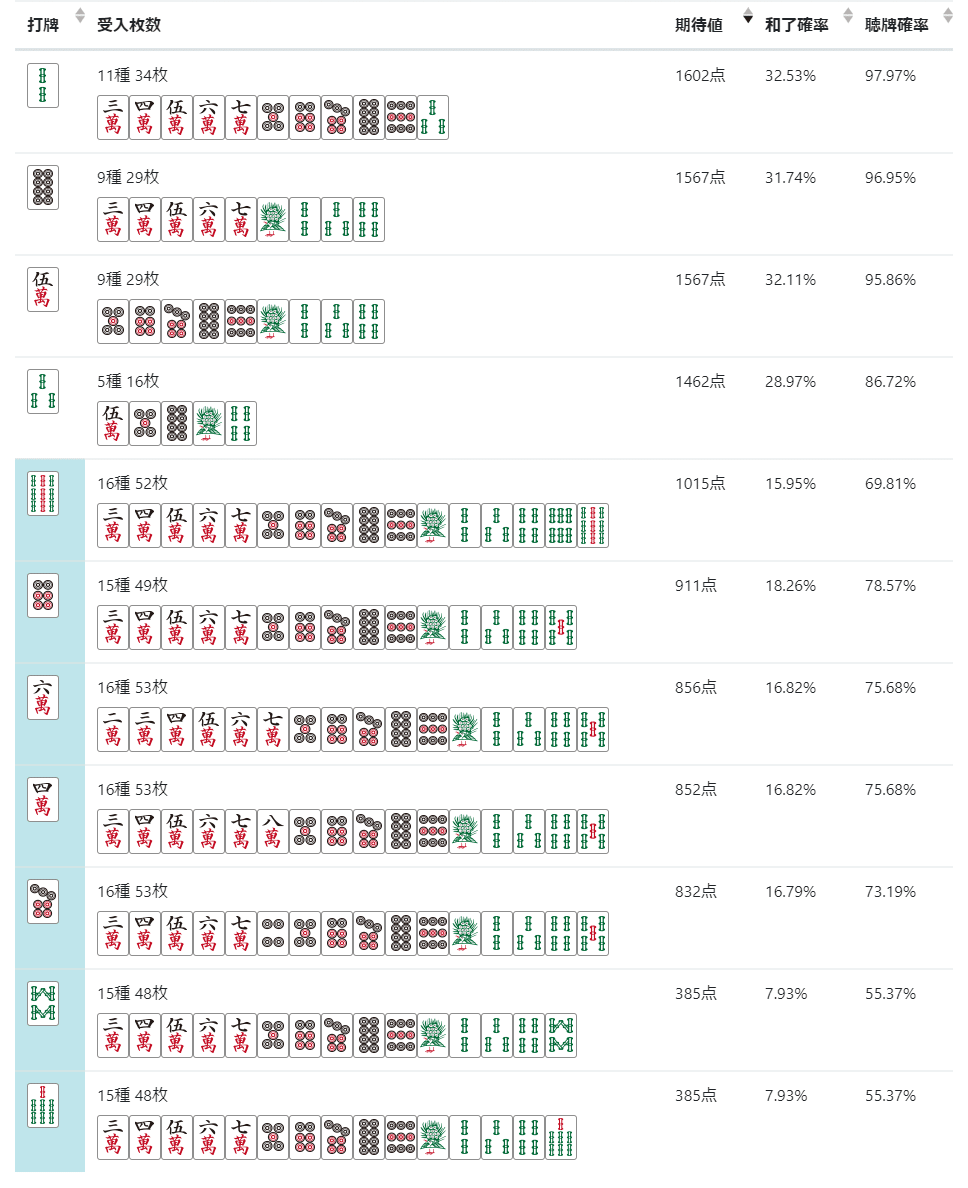
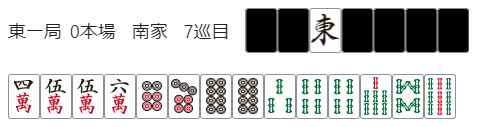

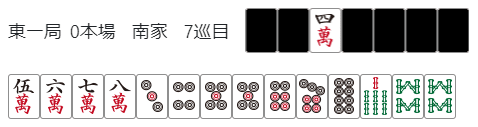
これは亜両面が一路端によっている形での「中ぶくれ+亜両面+両面トイツ」形です。
この2つの牌姿はよく似ていますが、これらに当記事の結論をそのまま適用すると、この形からはいずれも打5mになります。
シミュレーター的には打5mは全然悪いとは思えないんですが、pystyleさんシミュレーターで一番良いとされる打牌は上が打2sなのに対して、下は打8pとなっています。いずれも打5mではありません。
というわけで、この2つの差がどこから来るのかという質問です。
ちなみにツモアガリ確率計算機だとそうでもないようにも見ます。ここら辺は微差すぎて私にはよくわかりません。
pystyleシミュレーターがどう考えているのかについて考えてみます。
まず考えられるのは、単にフォロー牌同士の差です。
しかし、実際にやってみると単純な比較でpystyleシミュレーターと同じ結論は出てこないように思います。
たしかに、各ブロックを「メンツ(トイツ)+フォロー牌」と捉え、そのフォロー牌同士を比較すれば一見、瞬時に結論が得られるようにも見えます。
例えば、4556m(5m)、6788p(8p)、233s(2s)で、( )をフォロー牌とすると、
5m>2s=8p
となり、亜両面禁忌>中ぶくれ禁忌で
打2sとなりそうにも見えます。
ただ、これは次のような反例があります。


上の牌姿だと2sが明らかに機能が低いのですが、数値上この形はあくまでも亜両面否定が強いように見えます。ちなみにツモアガリ確率計算機の+1枚だと2sのようです。
この28牌や19牌がフォローになっている形については私も以前から気にはなってたのですが、理由をうまく説明できませんでした。
亜両面を①浮き牌+②面子と見て(4456sなら①4s+②456s)①が19の牌なら亜両面切り、34567なら両面対子を雀頭固定、28は不明。三色が絡む場合に中膨れ否定が現れることがある。
— まだちぃ。 (@madarasensei) December 24, 2020
以前200パターンくらい調べたが境目はこの辺の牌姿らしい
4556m2234p223789s ドラ8m
ヒロポンさんの説明




私の理解
要は、「中ぶくれ+亜両面+両面トイツ」は
原則がトイツ固定で、例外が亜両面否定になる。
例外の条件には2つあって
①亜両面が端のとき(19亜両面のとき)
②28亜両面、かつ両面トイツのフォロー牌が3~7のとき
(要は亜両面のフォロー牌<両面トイツフォロー牌)
ということだと理解しました。
何が問題か 両面トイツの意味
問題なのは、344+中ぶくれの形だと、2を引いたときでも中ぶくれをへこませれば最終形を亜両面にできます。
これが端の両面トイツ(233 or 778)+中ぶくれの形だと、
両面トイツの両面部分が埋まっても最終形を良形に取れません。
つまり、そもそも両面トイツとして持ってる意味があまりないのです。
そうであるなら中ぶくれ形を最初からへこまさないで、両面トイツをトイツ固定して一盃口で打点を見た方が良いということではないかと思います。
この「中ぶくれ+亜両面+両面トイツ」形に関しての結論が原則禁忌拒否なのか、トイツ固定なのかについて、シミュレーターの違いも含めて私にはまだいまいち核心が掴めていないのですが、ヒロポンさんの説明はすごい説得力だと思いましたので追記しておきます。
問題自体は非常にトリビアルなのですが、このような冷静で詳細な検討してくれたヒロポンさんに感謝をしています。
(2022.3.26追記)
