
MTシステム (マハラノビス・タグチシステム) ~品質工学におけるパターン認識~
以下のURLにてMTシステムを計算する機能限定のお試し版のExcelマクロを公開しております。
ExcelファイルをZIPで固めております。DLしてご利用ください。マクロが入っているので、ファイルのプロパティから、セキュリティで許可するのチェックボックスを☑にしてください。
この動画にて、上記マクロの使い方を紹介しております。
本ソフトウェアは、ExcelVBAにて作成された、小規模なMT法を計算するツールです。
※無料版のため機能限定しています。
メンバー数(データ数、行数)は100行まで
項目数(列数)は20列まで。
制限なしのバージョンは、品質工学会に入会すると、会員1人につき、1台のパソコンに無料でインストール可能になります。 制限なし版は、メンバー数、項目数無制限、直交表による項目診断・項目選択が可能です。(直交表L128まで対応)
Excelベースのパラメータ設計・SN比の自動計算ソフトも品質工学会員になると、MTシステムのソフト同様にインストール可能です。 もしご興味を持たれましたら、品質工学会にご入会下さい。
そして、入会はハードルが高いなーって思ったそこのあなた!
なんと解析支援ツールが無料(使用期限あり)で使えます!
上の方で紹介したマクロの正式版(フル版)です!
↓ ↓
解析支援ツールお試し版
こちらは、ツールの使い方、MTシステムの概念などをかいつまんで説明している動画になります!
YouTubeのマンガ動画の方もよろしく!
・~・~・~・~・~・~・~・~・~
~もくじ~
第1章 品質工学とは
1.1 品質工学を一言でいうと?
1.2 品質工学の哲学とは
第2章 MTSとは
2.1 MTSを一言でいうと?
2.2 パターン認識とは
2.3 MTSが適用できる範囲
第3章 とりあえず計算してみよう
3.1 解析の大きな流れと言葉の定義
3.2 MT法による小さい単位空間の計算
3.3 マハラノビスの距離の計算
第4章 実際のデータの場合
4.1 MTSの哲学
4.2 MT法の単位空間の作成
4.3 単位空間の信頼性の評価
第5章 項目選択
5.1 項目選択とは
5.2 直交表による項目選択
5.3 項目選択のテクニック
第6章 MTS法のこれから
6. 1 測れないものは作れない
<著者あとがき>
・~・~・~・~・~・~・~・~・~
第1章 品質工学とは
ここでは、品質工学を知らない人を対象に品質工学の概念について少しだけ触れておく。すでに品質工学の概念を知っている方は、読み飛ばしていただいてかまわない。
1.1 品質工学を一言でいうと?
よく「品質工学を一言でいうと?」と聞かれるが、これは非常に難しい。説明する時間が1時間あっても、理解してもらえるか怪しいものである。ある先生は、「そういう時は技術を効率よく評価する方法と言えばいい」、とおっしゃっていた。要するに、あなた自身の作った(考案した)技術を客観的に、効率よく評価できるということである。しかし、正しい品質工学の使い方をした場合のみ、この言葉は当てはまるのである。品質工学を、ただのツールとしてしか見ないで、計算方法だけまねをしても、まともな結果は得られない。また、そういうツールとしてしか見ない人に限って、「品質工学は使えない」という判断を下す。品質工学の品質工学ではない部分が計算方法(ツール)である。品質工学は工学という名前がついているが、すべてはいくつかの哲学のもとに成り立っており、その哲学を理解して初めて、品質工学を知ったということになる。
「品質工学を一言でいうと?」と聞かれたら私はこう答える。
「品質工学は哲学です。」
1.2 品質工学の哲学とは
少し品質工学を知っている人に、よく「実験計画法とどうちがうの?」という質問をうける。品質工学には哲学があるが、実験計画法には哲学が無いのである。前でも述べたが、品質工学のオリジナルな部分は、「哲学がある」ということである。直交表やSN比は、品質工学で生み出されたものではない。直交表は実験計画法でおなじみである。SN比はシグナル(signal)とノイズ(noise)の比で、主にステレオやカセットテープでおなじみ(音量を上げたら、雑音はどのように変化するかを見たもの)である。このSN比と区別するために、本当の単位表記はdBだが、品質工学ではdbと、わざとbを小文字で書く。これらの直交表やSN比は、品質工学の哲学を効率よく具現化するのに、今のところ有効なツールなので、使っているだけである。
図1-1 欲しい音・いらない音
では、品質工学の哲学とは何か。その一例をあげると…
「品質が欲しければ品質を測るな」
「欲しいはたらき(機能)を測れ」
これらの哲学の説明のために、モーターの例を挙げる。ここに、非常に品質の悪いモーターがあったとする。さらに、現在のエネルギ(電力)の配分は図1-2のようになっていたとする。
電力(100%) = 回転(40%)+振動(30%)+音(20%)+熱(10%)
モーターで欲しいのは回転である。それ以外は必要の無いノイズ(品質)である。例えば、哲学に反し、音のみを測定した1因子実験による最適化を行い、図1-3のように、音は小さくなったとする。
電力(100%) = 回転(50%)+振動(10%)+音(0%)+熱(40%)
音は小さくなったが、音に使われていたエネルギは他の所に回る。今度は熱の問題をなんとかしなければならなくなる。またもや哲学に反して、熱だけ測定した1因子実験による最適化を行ったとしよう。
電力(100%) = 回転(50%)+振動(20%)+音(20%)+熱(10%)
確かに、熱エネルギは小さくなったが、入力の電力は一定なので、熱に使用されていたエネルギは、音や振動のエネルギとして現れる。(図1-4)

図1-2初期のエネルギ-配分/図1-3 音が無くなったが/図1-4 熱は小さくなったが
結局もとの木阿弥である。このような実験を、品質工学的には「もぐらたたき実験」と言う。あちらをたたけば、こちらから問題が首を出す様を、よく表している言葉だと思う。このように、品質を測った実験では、対象としたものは良くても、対象としていない品質の問題が出てくるのである。
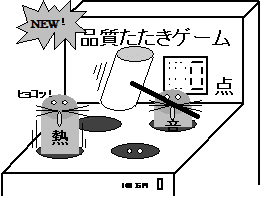
図1-5 品質のもぐらたたき実験
では、どうすればいいのか。ここで先ほどの「品質が欲しければ品質を計るな」「欲しいはたらき(機能)を測れ」という哲学が出てくるのである。ここでの品質は、振動、音、熱である。これらを測らないとすると、後は回転を計るしかない。つまり、回転=欲しいはたらき(機能)である。ここで、モーターは理想的には、全ての電力が回転エネルギになればいいのだと考える。
電力(100%) = 回転(100%)+振動(0%)+音(0%)+熱(0%)
ということで、電力と回転の関係を見た実験をすればいいのである。入力が全て欲しい出力に変換されるようにすれば、音や振動や、熱にエネルギが行かないような状態が作れるはずである。0%になるというのは無理であるとしても、この品質工学の考え方で実験をすれば
電力(100%) = 回転(70%)+振動(10%)+音(10%)+熱(10%)
という具合になることがある。(図1-6)
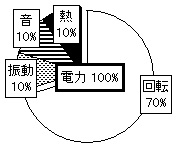
図1-6 最適化された状態
多くの人は、出て欲しくない音、熱、振動、ばらつき、不良率などを測って実験をしている。確かに測り易いのだが、本当に最適化できているのかは怪しい。最適化できても、多くの時間がかかるだろう。「品質が欲しければ品質を測るな」の一言には、これだけの重みがある。
では、音が聞こえないように、消音材料を詰めればいいじゃないか、振動しないように補強すればいいじゃないか、という声もある。しかし、それではコストアップにつながるうえに、音や振動の問題を「解決した」と言えるのだろうか?結局は、音や振動の原因を取り除いたわけではない。ただその場しのぎで、隠しているだけにすぎない。エネルギの流れは何も変わってないのである。
膨らんだ風船を、穴のあいた小さい箱につめるとしよう。もとの空気量は一定なのに、穴から出た風船を押さえようとすると、あちこちに無理が出てくるのと同じように、いくらその場しのぎで補強などをしても、いつかその問題は形を変えて、別な所に現れるのである。
図1-7 無理に補強しても、後で 問題が発生する
この他にも、以下のような哲学が存在する。
「実験にはすすんで誤差を入れろ」
「機能(欲しいはたらき)はエネルギの流れで考えろ」
「寿命試験は無駄だ」
「品質工学は技術の評価方法」 など…
品質工学が難解といわれている原因はこの哲学があるためだと思う。他の評価技術では、本に書かれている通りに計算していればよかったが、品質工学はそうではない。自身で考えるということが必要なのである。品質工学の本に書いてある通りに計算しても、品質工学を使っていないのである。
そのためか、普通の技術者ならまず、拒否反応を示す。考え方の枠組みから変えないと、簡単には理解できないだろう。また、かなり経験則に近い哲学なので、これらは文章や口で言うより、実際に実験をして経験してもらった方が理解できると思う。よって、ここでの品質工学の詳細な説明は省かせていただく。これらの哲学を理解し、その哲学もとに実験を行って初めて、品質工学を使ったといえる。
MTSも例外ではない。その根本には品質工学と同じ哲学がある。それを覚えていて欲しい。
第2章 MTSとは
本章では、主にMTSの計算以外のことについて触れておく。MTSとは何か?従来の方法とどう違うのか?どのようなことに適用できるのか?等について述べる。
2.1 MTSを一言でいうと?
「MTSを一言でいうと?」と聞かれたら「MTSはパターン認識です。」とでも答えようと思っている。まず、MTS(マハラノビス タグチ システム)の名前の由来から説明しよう。
今から50年ほど前、インドの数学者であるマハラノビス氏がマハラノビスの(汎)距離という統計学の手法を編み出した。これは統計の判別手法である。2つのデータ群があり、ここに新しいデータが1つあるとする。この新しいデータがどちらに属するかを判定するのに使われる。主に官能検査の多変量解析や主成分分析等の本を開けば載っている。タグチは、言わずと知れた品質工学の生みの親の田口玄一氏である。品質工学の哲学を生み出した方である。マハラノビス・タグチ・システム(MTS)は、これらの名前の頭文字を取って名づけられたものである。
別に、マハラノビスの距離自体は新手法というわけではない。パソコンの処理能力の向上により、大きな行列計算ができるようになったので、最近注目を集めているだけなのである。実は、数十年前に実際に健康診断に適用したという話があり、当時はパソコンの処理能力の限界から、200個程度のデータしか扱えなかったらしい。現在では、データ数が1000個でも2000個でもごく普通のパソコンを使って、解析できるようになっているので、その点は心配せず容易に行える時代になっている。
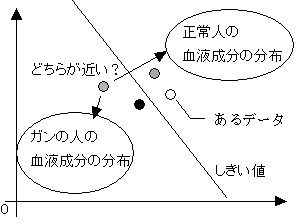
図2-1 マハラノビスの(汎)距離
2.2 パターン認識とは
さて、それでは「パターン認識とはどんなものか」ということについて説明を加える。文字認識の例をあげよう。図2-2の文字をみてもらいたい。
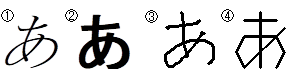
図2-2 文字の図
普通の人なら、①~④は「あ」という文字に見えるはずである。では、なぜあなたはこれらの文字が読めたのだろうか。これは人間の脳の中に文字に関するデータベース(経験)があるからである。それにより、「あ」という文字が経験上、一番「近い」「似ている」と判断したからである。ここで重要なのは「近いもの」であり、まったく「同じもの」ではないということである。「あ」1つに対して、パソコンでさえ、明朝体、ゴシック体、草書体、行書体、丸文字体、と様々な形がある。手書き文字ともなれば同じ形をしたものは、もはや1つもない。
他の例をあげれば、赤ちゃんが母親とそうでない人を見分けるのもパターン認識である。生まれたころは判断できないが、成長するにつれ人見知りを始める。つまり、赤ちゃんに人を見分けるだけのデータ(経験)が集まった、ということである。母親も、毎日まったく同じ顔をしているわけではない。それでも、ちゃんと見分けるのである。
天気予報も実態はパターン認識である。気圧や雲の状態が、過去の例と似ているかどうかを調べて、それに天気予報官の長年のカンが加わって、天気予報が行われている。気圧や雲の状態を調べて、過去の状態と照らし合わせるのはもちろんパターン認識であるし、天気予報官の長年のカン自体もパターン認識である。
われわれとて、簡単な天気の予想ぐらいはできるだろう。昨日が晴れで、今日の朝が晴れならば、午後も晴れると思うし、昨日が晴れで、今日の朝が雲が多ければ、午後は雨がふるかもしれないと思う。しかし、昨日が雨で、今日の朝が曇りならば、午後は晴れるかもしれないと思う。これは、その現象の理由を知らない子供でもやってのけることができる。つまり、われわれは、表2-1のようなパターンを経験上持っているのである。(少なくとも、私はこういうパターンを持っている。)ちなみにこれは、時系列データのある場合のパターン認識である。
表2-1 天気のパターン

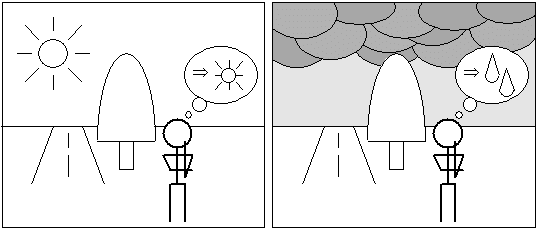
図2-3 今日の午後の天気の予想
このように、今まで蓄えたデータベース(経験)になんとなく「似ているもの」と判断するのが「パターン認識」である。今までのシステムだと「同じもの」か「違うもの」か(デジタル)の判断は得意だったが、「似ているもの」(アナログ)を判断するのは比較的難しかった。それがMTSにより「似ているもの」の評価ができるようになったのである。
少し統計をかじっている人から、主成分分析と比べてどうか、という質問を受ける。主成分分析は、個人の主観で項目に名前をつけて評価している。よって、主観が間違っていれば間違った結果になる。MTSでは、全ての項目についての関係を見ているので、主成分分析より客観性が高い。または、全ての方向について主成分分析をしたのと、同様の結果が得られると考えてもらってもいい。
また、今までの手法でよく使われてきた評価手法は回帰式であり、ある式の変数に値を入れると、答えが出てくるようなものだった。つまり、変数はそれぞれ独立であり、変数間に何も関係はない。MTSでは、全ての変数が関係付けられていて、ある変数の値に対して、他の変数もその値の影響を受けるのである。変数の交互作用のカタマリなのである。つまり、「組み合わせ」、もしくは「パターン」により評価しているのである。
・回帰式の場合
aX+bX+cX=Y
各変数A、B、Cは独立で、Xの値は各変数と比例関係を持っている。
・MT法の場合
Fa(b,c)+Fb(a,c)+Fc(a,b)=Y
各変数は独立ではなく、aはbとcの関数であり、bはaとcの関数であり、cはaとbの関数である。a1つが変化すれば、それはbもcも変化するのである。Yは各変数と比例関係を持っていない。これが交互作用である。
2.3 MTSが適用できる範囲
それでは、MTSはいったいどのようなことに使えるのだろうか。私自身は、判断、予測に関するものは、ほぼ適用できると考えている。人を見分ける、文字を見分ける、ムラを見分ける、病気かどうかを見分ける、人間の能力を見分ける、等々である。もちろん工場で良・不良を人間や機械が判断しているような部分には使えると考えている。さらには、地震予測、来年の健康状態の予測、天気の予測、1着2着の馬の予測…。他には、さわり心地、おいしさ、暖かさ等の官能検査の分野にも有効である。
図2-4 さて、あなたの予想は?
ここまで聞くと、すばらしい手法のように思えるが、そんなに甘くはない。MTSで病人かどうか判断しようとした場合では優秀な医師が必要であるし、天気予報をしようとした場合では、優秀な天気予報官が必要である。もし彼らの能力が低ければ、それなりの結果しか得られない。将棋の強いプログラムを作るには、将棋の達人が必要なのと同じである。
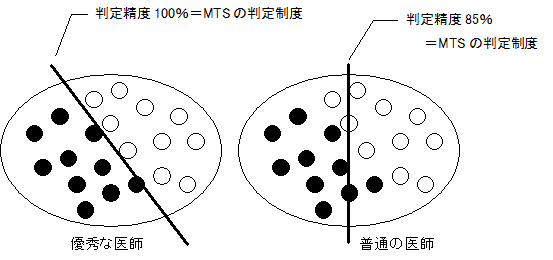
図2-5 医師の能力によって、健康のしきい値が変わる(●:病人 ○:健康人)
とどのつまり、単位空間を作成した人の判断能力が、そのまま判定精度になるのである。もし、これからMTSを何かに適用して、うまく行かない場合でも、それはMTSが悪いのではない。単位空間を作成した人と、判定者が悪いのである。品質工学のパラメータ設計と同じである。パラメータ設計をしてうまくいかないのは品質工学が悪いのではない。まずい基本機能を考えた技術者が悪いのである。
もしかすると、パラメータ設計も、MTSも、技術者の能力評価なのかもしれない。
第3章 とりあえず計算してみよう
この章では、MTSの中のMT法(相関行列の逆行列)の解析の流れについて説明をする。とにかく、MT法はどういう流れで、どんな計算をして、どのような結果が出るのかを捕らえてもらいたい。なお、もっとも重要な単位空間の定義方法や細かいテクニックについては4章で述べる。
3.1 解析の大きな流れと言葉の定義
ここでは、「文字認識をするための単位空間を作成する」として話を進める。それにはまず「あ」のデータベースが必要になる。つまり様々な「あ」のデータを集める必要がある。明朝体、ゴシック体、草書体、行書体、丸文字体、手書き文字まで含めれば多くの「あ」を集めることができる。これらはデータといい、その集めた数をメンバーという。
次に、「あ」の特徴を何かしらの手法で数値化する必要がある。例えば交点の数や、黒い部分の座標位置、囲まれた面積、等々である。これらを項目と呼ぶ。交点の数という項目ならば項目数は1個、もし「あ」の文字を14×13分割して、その部分が黒か白かという項目ならば、項目数は14×13=182個というようになる。(図3-1)

図3-1 「あ」の生データ
もし、交点の数と、分割した目の白黒の2種類を項目とするならば、項目数は、1+182=183個となる。(表3-1)
以上の作業により、「あ」のデータベースができる。MTSでは、このデータベースを単位空間データという。この単位空間の定義がMTSでもっとも重要なので、4章でじっくりと述べる。
表3-1 データベース(単位空間データ)
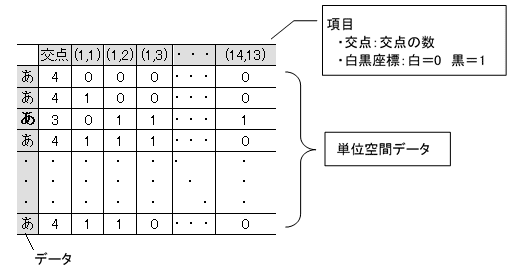
この単位空間データに、ある計算を施し、マハラノビスの空間を作成する。このマハラノビスの空間を単位空間と呼ぶ。計算方法は3章2節で述べる。
次に、「あ」かどうかわからない文字「?1」「?2」「?3」を持ってくる。この「?1」「?2」「?3」がこの単位空間からどれだけ離れているかを計算する。この、どれだけ離れているかという距離をマハラノビスの距離という。もちろん「?1」「?2」「?3」も、単位空間データと同じ項目で数値化されているものとする。距離の計算方法は3章3節で述べる。
表3-2 「?」のデータ

さらに、単位空間に使用したデータも、単位空間からの距離を計算する。その結果をヒストグラムにすると、図3-2のようになる。単位空間に使ったデータは、おおよそ1前後に分布するようになる。
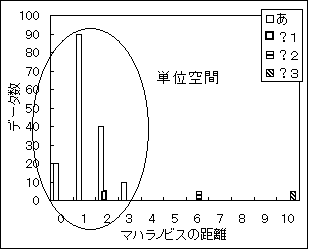
図3-2 「あ」と「?」の単位空間からの距離
このようになった場合、それぞれの「?」はどんな文字だろうか。
・「?1」は単位空間に収まっているので、「あ」であると判断してもいいだろう。
・「?2」は単位空間から少し離れているので、「め」や「お」といった文字であると考えられる。
・「?3」はあきらかに単位空間から離れているので、「あ」以外の文字であることが想像できる。
…と、いうように判断できる。また、しきい値を、例えば「5以下は「あ」である」と決めれば、客観的に数字で判断することが可能になる。
ただし、「?2」はもしかすると、汚い手書きの「あ」かもしれない。ではどこまでが「あ」でどこから「あ」ではないのだろうか。しきい値は5にすればいいのか、7にすればいいのか。これは技術者が自由に決めることができる。しきい値は、「あ」を「あ」と判断しない場合と、「め」を「あ」と判断する場合のコスト(社会的損失)などで決めればいいことである。
3.2 MT法による小さい単位空間の計算
ここでは、手計算でできるぐらい小さなデータを使い、どのような計算をしているのか「なんとなく」わかってほしい。実際はとても手計算は不可能である。現在はMTSのソフトも数種類販売されているので、それを利用するといい。(統計のマハラノビスの(汎)距離を計算するソフトとは別である。)難しい計算も無いので、自分でプログラミングしてもかまわない。
さて、ここにAとBというセンサが2つあるとする。このセンサでデータを取ったら、表3-3のようになった。このデータを使って、単位空間を作成してみよう。
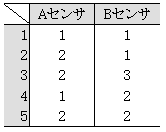
表3-3 センサの生データ
まず、データを基準化するために、平均と標準偏差を求める。
平均
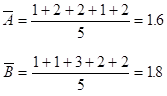
標準偏差
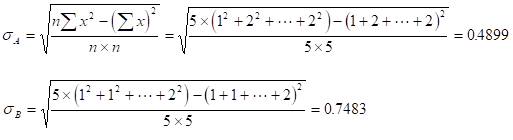
これら、平均と標準偏差を使い、基準化値 を求める。
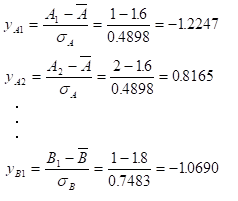
表3-4 平均、標準偏差、基準化値
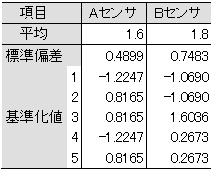
以下、同様に計算すると、表3-4のようになる。これで、全ての項目において、1を中心として均等に分布するデータに変換することができた。
次に、基準化したデータを用い、個々の項目のデータの相関を求める。基準化されていることにより、相関係数は次の簡単な式で求めることができる。
センサAとセンサBの相関係数
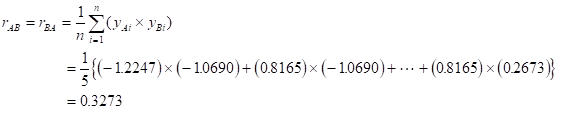
これを全ての組み合わせ(AA,AB,BA,BB)で行う。すると、次のような相関行列ができる。自分自身に対する相関は1なので、斜め成分は全て1になる。
相関行列
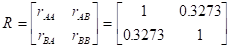
さらに、この相関行列 の逆行列を求める。
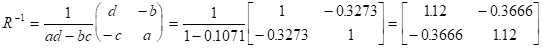
この逆行列 が最終目標の単位空間である。
3.3 マハラノビスの距離の計算
前節で単位空間ができた。では、この単位空間からの距離を求める。
表3-5、表3-6において、1~5は単位空間作成に使用したデータ、?1、?2は新しいデータである。まず、データの基準化を行う。ただし、基準化を行う場合の平均値と標準偏差は単位空間作成に使用したデータの値を使い、計算する。
「?1」のセンサAの基準化値と「?2」のセンサBの基準化値は、

表3-5 センサの生データと、新しいデータ
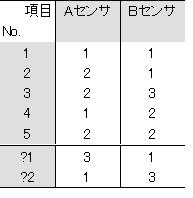
表3-6 基準化されたデータ
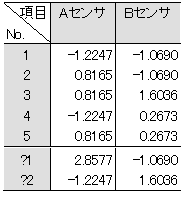
表3-5のNo.1の場合のマハラノビスの距離 は
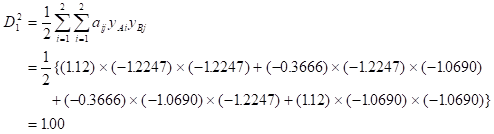
表3-5の「?1」の場合のマハラノビスの距離 は
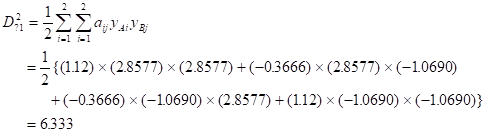
以下、同様に計算を行うと、表3-7のようになる。
表3-7 マハラノビスの距離

さて、ここで単位空間に使ったデータの距離の平均を求めると、
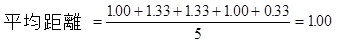
…となる。このように、単位空間のデータは1を中心に分布する。もし、これが1にならない場合は、どこか計算を間違っているはずである。コンピュータに計算させた場合でも、桁落ちなどで1にならない場合がある。あまりにも1から外れた数字ならば、計算を見直す必要がある。1~5の距離に比べ、「?1」や「?2」は見ての通り、1より大きな数字になる。実際に生データを見ても正常とは異なるデータであることがわかると思う。
以上が2次元(項目が2個)の場合の計算である。しかし、センサが10個あれば10次元(項目が10個)となり、10×10の逆行列を計算しなければならず、とても手計算はできない。
第4章 実際のデータの場合
本章では、本格的にMTSの細かい内容まで説明を加える。第3章の話をより掘り下げたものだと思ってもらいたい。
4.1 MTSの哲学
MTSでは単位空間の決め方が最も重要である。パラメータ設計で、基本機能を決めるのが最も重要なのとまったく同じである。これが間違っていれば、何も評価できない。では、どのように単位空間を決めて、どのようなデータを取ればいいのだろうか。その答えは「安定したものを基準にする」の一言である。通常、我々は問題点について研究をすることが多い。しかし、それはノイズであり、非常に多くのばらつきがある。さらに問題点の種類そのものが多い。
例えば、病気か病気ではないかを考えた場合、どちらが安定した状態だろうか。病気ではないという状態はかなり安定していると考えられる。病気という状態は、まず病気の種類だけ状態が存在する。もはやこれだけで安定している状態とは言いがたい。さらに同じ病気でも、症状の重さによって、いくつかの段階に分かれる。もはや、収集がつかない。さらにそれがどの部位なのか?胃なのか?肺なのか?喉なのか?もうわけがわからない。
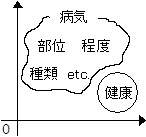
図4-1 健康はまとまっているが、病気は?
もう1つ例をあげる。ある生産工程で、製品を作っているとする。良品と不良品、どちらが安定しているだろうか。明らかに良品が安定しているだろう。不良品という状態は、寸法が大きい、色が変、動作しない、etc.…。あげればきりが無いうえ、全ての不良条件をあげ切れるとも思えない。また、それがどの程度なのかということも考えると、もう無限大である。

図4-2 1つ駄目なだけで不良品…
もちろん、安定していないものを単位空間にしてもかまわない。ただし、それでは判定精度は落ち、ただ統計のマハラノビスの(汎)距離の計算をしているに過ぎない。また、安定しているからといって、太陽の黒点の数と、経済成長率の関係をみても、あきらかに因果関係がないので意味が無い。当てはめではない、確かに因果関係のあるデータを使うべきである。
MTSで勘違いして欲しくないことがある。MTSは、測定しにくいものを測定する手法である。今までの手法で測定できるなら、わざわざMTSを適用する必要は無い。また、不良率の予測に適用するなどは言語道断である。いくら予測できても、不良率が減るわけではない。この場合は、MTSを適用するよりも、品質工学の手法であるパラメータ設計などを使い、最適化をするべきである。ただし、その不良判定が人間ではないとできないという場合は、MTSを適用するしかないであろう。そして、MTSにより客観的に測定できるようになったならば、その値を使い、パラメータ設計をして最適化をし、最終的には測定などしなくてもいい状態を作り上げるというストーリーが最もいいと思う。
MTSの哲学をわかっていただいた所で、次に単位空間と距離のイメージをつかんでもらおう。単位空間とは、データ群のかたまりで、数字では1前後に分布することは前にも述べた。距離とは、ある「?」データと単位空間(安定したデータ群)の重心までの距離である。ただし、ただの2点間(ユークリッド)の距離ではない。マハラノビスの距離では、データ群の分布に重み付けがされている。
山登りを考えてもらえばいい(図4-3)。同じ頂上でも、一般の登山道を登るのと、ガケを登るのでは意味が違う。一般の登山道では緩やかな勾配なので、頂上にたどり着くのは楽だが、道のりは長い。ガケでは勾配が非常にきついので、登るのは苦しいが、道のりは短い。ユークリッド(2点間)の距離では、道のりしか見ないので、○よりも●の方が頂上に近い。しかし、マハラノビスでは勾配(分布)も考慮に入れるので、○も●も同じ程度の距離となる。
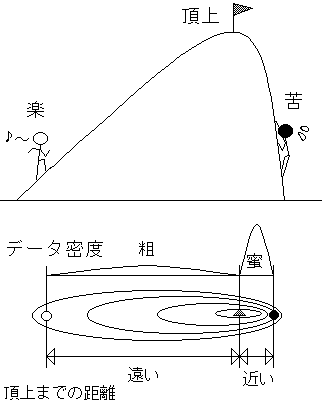
図4-3 マハラノビスの距離のイメージ1
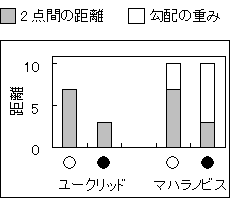
図4-4 ユークリッドの距離とマハラノビスの距離の違い
図4-3場合は2次元だが、3次元の場合はどうだろうか。図4-5を見ていただきたい。さて、AとB、どちらが頂上に近いと言えるだろうか。(a)の場合は、ユークリッドの距離でもマハラノビスの距離でも、AとBは同じ距離になる。ところが、(b)はどうだろうか。ユークリッドの距離ならば、Aの方がBより頂上に近いようだが、マハラノビスではAよりBの方が頂上に近いことになる。つまり、Bは分布に含まれるが、Aは分布の外なのである。実際にはマハラノビスの距離では、多次元のデータで、このように分布を見て、距離を計算しているのである。
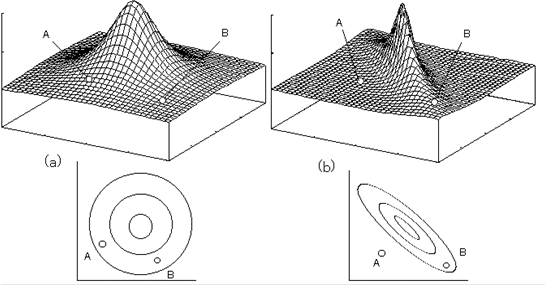
図4-5 マハラノビスの距離のイメ-ジ2
表4-1 ユークリッドの場合とマハラノビスの場合の距離の比較

4.2 MT法の単位空間の作成
実際に計算する場合は、以下のような注意点や制約が出てくる。
① 逆行列を計算するために、項目数よりデータ数が多くなければならない。
(例:項目数100個 < データ数150個)
② 1つの項目において、全て同じデータになっている場合は分散が0になり、以降の計算ができないので、その項目は外す。また、限りなく分散が0に近い場合も同様である。
(例:アンケートで、全ての人が男性だった。100人中、99人が同じ答えをした。)
③ 相関の高い項目(0.99以上)は2つのうちどちらか一方を使わない。もしくは、数学的にf(A,B)=f(C)のような関係のあるA,B,Cの項目も、どれか1つ外す。難しい言い方をすると、多重共線性が出るという。多重共線性があまりに強いと、空間が不安定になる。
(例:昨年の年齢と今年の年齢、A+B=Cや、A×B=Cなど。)
この3つをクリアしていれば、計算はできる。さらに精度のいい単位空間を作るには、
④ データ数は、できるだけ多く、最低でも単位空間のデータは200個以上は欲しい。ただし、これは経験上の話である。
(例:アンケートや感覚なら300個、良品・不良品判定なら200個)
⑤ プロフェッショナルが判断した境目(しきい値)で単位空間を作る。判定能力の無い人が分類したものでは、精度が期待できない。
(例:官能検査ならプロのパネラー、加工製品なら熟練した技術者)
⑥ MT法をよく理解している。
(例:このテキストを穴があくほど読んでいる・・・とか(^-^; )
さて、3章で出てきた式を、一般化すると次のようになる。得られたデータを とし、項目数を i=1,2,・・・,k 、データ数を i=1,2,・・・,n とする。まず、 Yijより平均値mi と標準偏差σi を計算する。
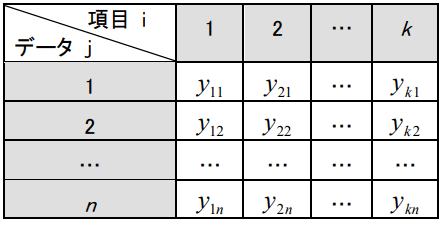
表4-2 得られたデータ
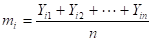
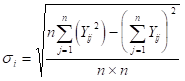
さらに基準化値Yijを求める。
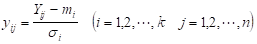
次に、基準化値 の相関行列 を求める。

ここに、
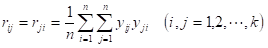
である。相関行列 の逆行列 の成分を とし、逆行列を とすれば、
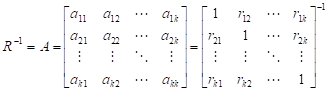
この が単位空間である。この単位空間の要素を使い、あるデータのマハラノビスの距離 を次式により求める。
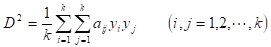
ただし、 は、単位空間の平均 と標準偏差 により基準化されているものとする。
…このようなものを見せられても、よくわからないと思う。こんな計算をするんだ、という程度知っていれば問題は何も無い。要はツールの部分なので、哲学の部分さえ知っていれば、後はどうでもいいのである。
4.3 単位空間の信頼性の評価
どんなデータでも単位空間を作ることはできるので、最後に確かめ算をしなければならない。つまり、単位空間の信頼性の評価である。ここで2つの計算を行ってもらいたい。
1つめは、単位空間までの異常データの距離を計算する。その距離が大きくなることを確認する。これが図4-6のように単位空間と重なるようでは、その単位空間の判定精度は無いと思っていい。しかし、ただ単に単位空間から異常データが離れているだけでは十分ではない。(図4-7)
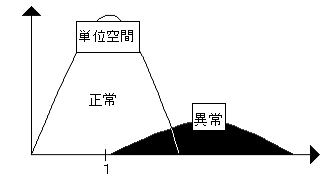
図4-6 判定精度の無い単位空間
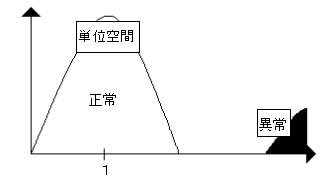
図4-7判定精度があるように見える単位空間
次に、単位空間作成に使用していない正常データの距離を求める。この距離を単位空間外データ距離という。ちなみに、単位空間に使用したデータは1前後に分布するようになっているため、単位空間に使用したデータでは単位空間の信頼性を調べることはできない。
単位空間外距離が図4-8のように単位空間から離れてしまった場合、この単位空間はやはり判定精度がないことになる。このようになったら、単位空間を作りなおす必要がある。
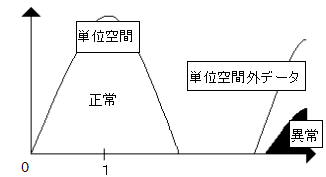
図4-8 どちらも離れてしまう単位空間
そして、良好な状態というのは、図4-9のように単位空間外距離が単位空間と重なり、異常とは離れている状態である。最もいいのは、単位空間外距離が全て単位空間と重なる場合である。
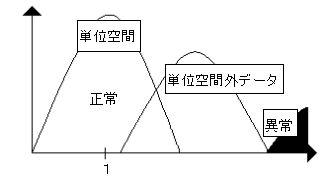
図4-9 良好な状態の単位空間
しかし、よほどうまい単位空間を作るか、非常に多いデータ数(2000個以上)があるか、単位空間が安定しすぎている場合にしかこの状態は見られない。
単位空間外データ距離であるが、もし単位空間のデータが300個程度と、たくさんあるならば、10個程度単位空間から外し、290個で単位空間を作成し、外した10個の距離がどのような分布になるか調べればいい。その分布が、図4-6~図4-9のどれに当たるかは判断できると思う。しかし、単位空間のデータが集まらず、100個や150個といった場合、10個も外しては、単位空間の判定精度が大きく落ちるのは明白である。だからといって、3個外して、97個で単位空間を作成して、3個の距離がどのような分布になっているか調べても、たった3個のデータでは信用できない。また、100程度ならば、3個外しただけでも、単位空間の精度が大きく低下する場合もある。では、どうすればいいのか? 現在のところ、以下の方法を推奨する。単位空間の信頼性の低下を最小限に抑えながら、単位空間の信頼性を評価する方法である。これはジャックナイフ法と呼ばれている。
まず、100個のうち、1個だけ単位空間からデータを外す。そして99個で単位空間を作成し、外した1個のデータの距離を計算する。次に、先ほどのデータは単位空間に戻す。今度は別なデータを1個外し、その距離も求める。以下、この繰り返しである。100回繰り返してもかまわないし、50回程度でやめてもかまわない。
もちろん、このような方法を取らなければならないような単位空間では、あまり判定精度は期待できない。やはり、単位空間のデータは、たくさん欲しいものである。
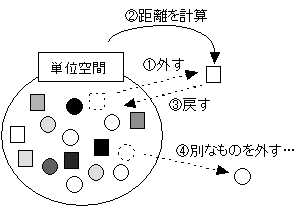
図4-10 単位空間のデータ数が少ない場合の信頼性の評価方法
あと、ごくまれに単位空間(正常)データなのに、1近辺の数字ではなく、10や20といった数字が出ることがある。単位空間外距離ならば、10や20というのは珍しくないが、単位空間のデータの距離が離れるのである。これは、その生データをみてみればわかるが、特異な正常データなのである。確かに正常は正常なのだが、全体的にまれな例の正常なのである。このような場合はまれな例のデータを増やすか、まれな例を単位空間から外したほうがいいと思われる。なにより、単位空間を安定させる必要があるのである。
また、全てのデータが、欠ける事なしに集めることができればいいが、そうはいかない場合も存在する。いわゆる欠測値がある場合には、どのように処理すればいいかである。もし、全体のデータ数に対し、欠測値が少ない場合(目安:50個に1個程度)ならば、そこに、単位空間の、その欠測している項目の平均を入れて解析してしまうのも手である。しかし、基本的には単位空間はものさしであり、そこにわざわざ誤差をいれるのは望ましくない。
10個に1個もあるようであれば、単位空間からその項目を外して解析する方がいい。ただし、単位空間からの距離を求める場合は、欠測値があっても、単位空間の平均を入れて解析すれば、欠測しない場合とほぼ同じ程度の距離が出るという研究報告がある。ただし、欠測している項目が重要な項目でない場合である。重要な項目が欠測していれば、もちろん正しい距離は出ない。
単位空間を作成したが、正常と異常がうまく分かれない場合、そこであきらめてはいけない。まず、正常と異常のしきい値を変えて、もう一度単位空間を作りなおしてみることを薦める。われわれが主観で決めたしきい値は、実際のしきい値とは異なっている場合が結構あるので、これで解決する場合がある。
しきい値をいくら変えても、正常と異常が分かれない場合は、単位空間を見直す必要がある。本当に正常としたものは安定しているのか?もしかしたら、異常としたものの方が安定しているのではないか?もしくは、正常と異常の中間の、普通というのが安定しているのではないか?判定方法はこれでいいのか?項目はこれでいいのか?重要な項目が抜けているのではないか?最終的には、正常、異常の分け方は正しかったのか? というとこまで確認するべきであろう。
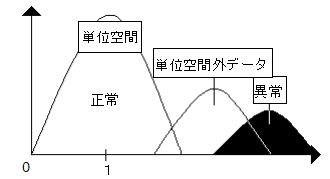
図4-11 判定があまりうまく行っていない場合
上記のことを確かめて、問題が無ければ、後は、データ数が足りないだけである。単位空間のデータ数が100個程度ならば、正常と異常が綺麗に分かれなくても不思議ではない。やはり、200個以上は欲しいものである。
最低限として、重なっていても、以下の3つの中心、単位空間の距離分布の中心、単位空間外の距離分布の中心、異常の距離分布の中心が離れていそうな場合は、まだ救いがある。将来的にデータを増やせば、離れるかもしれない。データ数が1000個とかあっても、このようになっているならば、確実に単位空間の決め方が間違っている。よく見直すか、周りでMTSに長けた人に見てもらい、客観的な意見をもらうのがベストである。
第5章 項目選択
4章までの話で、単位空間は作成できるようになり、距離も計算できるようになっているハズである。ここでは、できた単位空間に対し、項目の有効度をSN比と直交表を使い評価する手法を紹介する。
5.1 項目選択とは
項目選択(項目選定とも呼ばれる)は、単位空間ができた後、判定に有効な項目と、判定に必要の無い項目を調べる手法である。これにより、以下のようなメリットがある。
・判定に必要の無い項目を単位空間から外すことにより、計測コストを下げる。
・ 判定に必要の無い項目を単位空間から外すことにより、計算時間を短縮する。
・ 判定精度の低い単位空間の精度を向上させる。
・ 異常データの傾向を見ることができる。
ここでは直交表を使った項目選択の方法について解説する。
図5-1 必要なものと、いらないものを区別する
5.2 直交表による項目選択
ここでは、ある程度単位空間の信頼性が得られていることが前提条件である。そのデータを使い、項目選択をする。
まず、どのような計算をするのかというと、項目を2水準系の直交表に割り付け、直交表の第1水準は、「この項目を単位空間作成に使用する」、第2水準は「この項目を単位空間作成に使用しない」とする。そして、各行で単位空間を作成する。例えば、直交表L12ならば、第1行は全て1なので、全項目を使って単位空間を作成する。第2行では、前半分が1なので、半分の項目だけで単位空間を作成する。以下、同様に12個の単位空間を作成する。
作成した単位空間に対して、数個の異常データの距離を求める。検証する異常データは、多ければ多いほどいいが、異常データを集められない場合もあるので、実際には5~100個程度といった感じだろうか。文字認識ならば、「あ」ではない文字が異常データなので、簡単に集めることができる。しかし、火災用の煙センサの場合、正常を火災でない状態と定義した場合、異常は火事の状態である。しかし、そうそう火事のデータを取ることはできないので、このような場合は、異常データは少なくても仕方ないと思われる。
以上の作業により、表5-2のようになったと思われる。後はこの異常データの距離を使い、SN比を求める。SN比とは、最初の方にも述べたが、信号とノイズの比である。この場合の信号は、異常データの程度であり、出力は距離である。その出力の距離ばらつき方がノイズである。
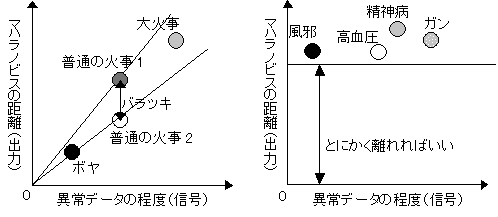
図5-2 信号因子の真値がわかっている場合/図5-3 信号因子の真値が不明の場合
異常データには程度がある。例えば、「あ」で単位空間を作成したとする。この「あ」の単位空間に、「あ」に似ている「め」や「お」といった文字のマハラノビスの距離を求めた場合は小さくでるだろうし、「あ」とまったく似てない「い」や「う」といった文字では、大きく出るだろう。また、火災用センサの場合は、ボヤと大火事の場合で距離が同じになるはずがない。さらに付け加えると、同じ病気でも、病気の重さによって単位空間からの距離が違うはずである。これを考慮した場合は動特性(0点比例の)SN比を求める。つまり原点を通る直線とそのバラツキを考慮した計算をする。計算式は以下の通りである。 nは異常データの数、Mはその異常データの程度(真値)である。注意して欲しいのは、 を にして解析することである。
表5-1 動特性の計算
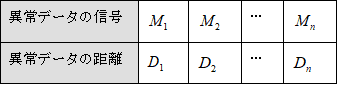
全変動
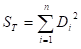
比例項の変動
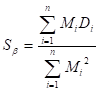
誤差変動
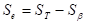
誤差分散
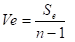
SN比
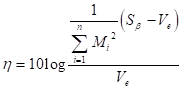
感度
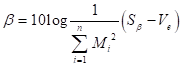
表5-2 L12直交表と計算データ
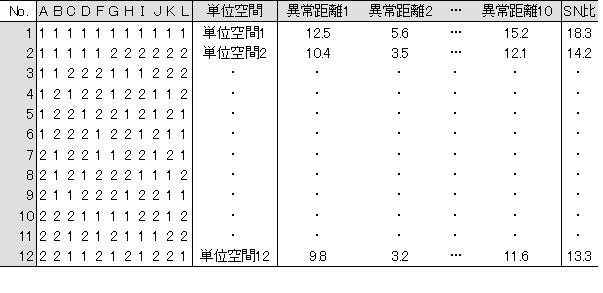
しかし、異常データの信号の真値がハッキリわかるのならいいが、だいたいしかわからない場合も存在する。火事の場合もそうだが、この火事は14、あの火事は17と真値が数字で出てくるわけではない。このような場合は、ボヤは5、普通の火事は10、大火事は20とだいたいの信号を決めてしまう。
ただし、中には異常の真値がまったくわからない場合もある。
例えば、健康人か病人か判断する場合、病人といっても、いろいろな病気があり、どの病気の重さを真値にすればいいのか不明な場合である。このような場合は、異常の程度は関係無く、ひたすら距離が大きくなってくれればいいと考える。一旦異常データの距離を計算し、それを真値とする。ただし、第2ステップとして、それぞれの異常が、どのような異常なのか調べる必要がある。図5-2でいうと、病気は病気でも、それが風邪なのか、ガンなのか調べなければ、対応ができないのである。調べるには、項目選択を異常データ1個で行う。その要因効果図の傾向から、どのような異常なのか、どこが健康人と違うのかというのを調べて判断する。これを項目診断と呼ぶ。

これで、SN比までの計算が終了した。次に、要因効果図を書く。つまり、項目を使用した、使用しなかったということで、SN比がどのように変化したか=マハラノビスの距離がどのように変化したかを見るのである。例えば、直交表L12ならば、
A1(解析に使用)=(1,2,3,4,5,6)のSN比の合計/6
A2(解析に未使用)=(7,8,9,10,11,12)のSN比の合計/6
B1(解析に使用)=(1,2,3,7,8,9)のSN比の合計/6
B2(解析に未使用)=(4,5,6,10,11,12)のSN比の合計/6
…
L1(解析に使用)=(1,5,6,7,9,12)のSN比の合計/6
L2(解析に未使用)=(2,3,4,8,10,11)のSN比の合計/6
というように、各項目で第1水準の平均、第2水準の平均を計算する。そのデータをグラフにすると、図5-4のようになったとする。
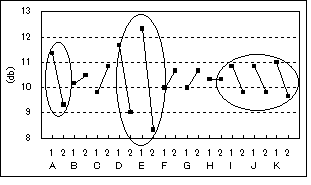
図5-4 要因効果図
SN比が高ければ、直線性があり、バラツキも比較的少ないということである。第1水準を解析に使用する、第2水準を解析に使用しないとしたので、左上がり(\)が判定に重要な項目で、右上がり(/)が判定に必要のない項目である。図5-4では、A、D、Eの項目が判定に重要な項目であるということがわかる。また、I、J、Kは重要ではないが、有効な項目、Hはどうでもいい項目、B、C、F、Gは判定に必要の無い項目である。
以上より、判定に有効な項目、有効ではない項目がわかった。後は、項目を減らしたいならば、判定に有効ではない項目を外して、もう一度単位空間を作成すればいい。それほど判定制度を落とすことなく、項目を減らせているハズである。
「ハズである」と書いたのには理由がある。個人的には項目を減らすことに、直交表を使うことに疑問を持っている。直交表は、交互作用がある場合は使えないのである。田口先生も、「MTSで取り扱うのは、全て交互作用のあるデータです」と言っている。前にも述べたが、Aという項目(変数)は独立ではなく、BやCという項目(変数)とある関係も持っているのである。ここで、Aという変数を使わなければ、BやCといった変数もその影響を受けるのである。つまり、項目選択で外せるのは、独立かつ効果の低い項目である。2水準系の直交表でわかるのは、効果の大きさだけである。効果が低いからといって、その項目を外しても、他の効果の大きい項目と関係があれば、最終結果として出る距離にまで大きな影響を与える。
例えば、図5-5の(a)のように、大きな円を支えている小さな円●でも、全体に与える影響は大きい。
しかし、(b)のように、他のものと影響の無い小さな円○なら、外してもなんら問題は起きないのである。とどのつまり、その1個を外したことにより、異常データの距離がどの程度変化したかを、注意深く見る必要がある。
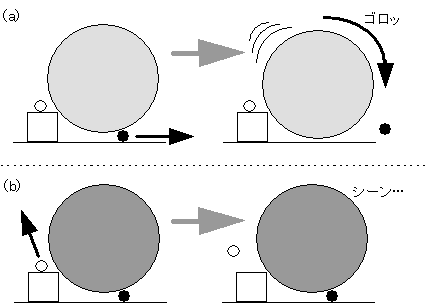
図5-5 外していいものと、外してはまずいもの
5.3 項目選択のテクニック
ここで、いくつか項目選択のテクニックを紹介する。
(1)有効な項目を固定する。
非常に重要だと思われる項目や、簡単に取れる(計測コストが安い)データを直交表の外に出し、毎回その項目を使うのである。それで項目選択を行えば、解析時間の短縮になる。使用する直交表が小さくてすむのである。しかし、最近は流行らない方法である。重要だと思われている項目も、本当に重要かわからないし、いくらコストが安いからとはいえ、判定に関係の無い項目があれば外しておきたいものである。
(2)項目選択を繰り返し、項目をさらに減らす
どこまで項目を外せばいいのか?これは結構、難しい問題である。1回の項目選択で外した項目と関係の深かった項目があった場合、関係の深かった項目も、もはや不要である。2回目の項目選択を行い、その項目を外すと、また判定に関係がないという項目が出てくる。しかし、ただ外せばいいという問題でもない。前述の通り、交互作用のかたまりなので、外すことにより判定精度が大きく低下する場合がある。図5-4の要因効果図の例ならば、水準(SN比)の平均はだいたい10.3dbといったあたりだろうか。2回目の項目選択で、この10.3dbがどの程度になるかが問題である。もしこれが8dbというように下がれば、外してはいけない項目を外してしまったことになる。10db程度なら、項目選択でいらない項目を外すことに成功したといえるだろう。動特性の場合はSN比と感度(傾き)の2つで評価しなければならない。いくら直線性(ばらつき)が抑えられても、感度も下がってしまっては、判定精度があるとは言いにくくなる。どんな信号を入れても、出力である距離は同じ値になってしまうからである。
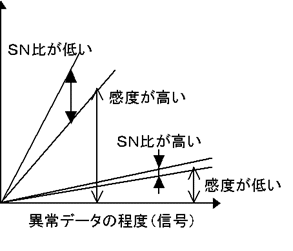
図5-6 動特性でみた単位空間の信頼性
また、計測コストと、項目の数とのトレードオフもある。センサーが多ければ多いほどコストもかかるが、判定精度もあがるのはあたりまえである。また、コストをかけないとはいえ、1個だけで判定精度を出そうというのも、虫のいい話である。適度なセンサの数(コスト)と、それに見合った適度な判定精度を決める必要がある。
(3)すべての項目が有効という結果が出た場合
結果通り、全てが有効なのである。しかし、どうしても項目を減らさなければならない場合もある。そのような時には、半分程度を核にして、1つ小さな直交表で解析するのである。おそらく、これで2~3個は判定に必要の無い項目が出てくるはずである。その2~3個は、交互作用の効果で必要と出ていた項目なのである。
別な方法として、比較的効果の小さい項目を外してしまうのも手である。この方法でも、2~3個は判定に必要の無い項目が出てくる。ただし2回目の項目選択では、1回目に外した比較的効果の小さい項目を単位空間に戻しておくことを忘れないで欲しい。効果が小さいからとはいえ、判定に有効な項目であることには間違いないからである。
第6章 MTSのこれから
この章では、無謀にもMTSのこれからの展開について私なりのコメントを加える。参考程度にとどめて欲しい。
6.1 測れないものは作れない
忘れてはならないのは、「MTSはものさしに過ぎない」ということである。いくら測っても、不良を見つけることはできても、不良を減らすことはできない。では、なぜMTSが必要となるのか。それは「測れない」「測りにくい」ものがあるからである。人間の能力、感覚といったものを始め、1次元的に評価できないのもが世の中には、結構あるものである。そのような多次元的なものには、多次元のものさしが必要になるのである。多次元のものさし=MTSなのである。
ただ、最近目立つのは、測れるのに、わざわざMTSを使う事例が多いことである。それはまったく意味が無い。そのものの機能(基本的なものの働き)を考えずに、MTSに頼るのは考え物である。まずは、機能を考え、それでだめならば、最後の砦としてMTSを使うのが、MTSの正しい使用法だと思う。
パラメータ設計ができない分野では、どうだろうか。金融機関による、融資の判断。能力評価などが例として挙げられるだろう。お金を貸して、返してくれる人。さらに、お金を貸して、一定期間空けてから返してくれる人。銀行としては、後者の方がありがたいのである。たっぷり利子が取れるからである。しかし、返してくれない人は困る。これらをどのように判断するか。ここでMTSが出てくるのである。アメリカではすでにMTSを、融資の判断に適用した研究が始まっているらしい。
能力評価はどうであろうか。人間もパラメータ設計はできない。できないならば、最初から能力のある人を取るしかない。アメリカの大学で、入試試験の成績と、卒業時の成績の相関を調べた人がいる。その結果、相関はないという結果が出たらしい。会社から見た大学の評価は、能力のある卒業生がいるかどうかである。別に入学時に成績が、よかろうが、わるかろうが、会社側は関係ないのである。ならば、大学はどうすればいいか。卒業時に能力が高くなる学生を入学時に予測できればいいのである。ここでMTSを使うのである。他にも、入社時のテストにMTSを使ったりすることも、可能であると思われる。ここまでくると、もはやIQテストのようなものである。
シミュレーションでデータを得るのも手である。大量のデータが楽に手に入る。MTSで一番大変なのは、データを集めることである。これさえできてしまえば、あとはパソコンがほとんどやってくれる。ただし、シミュレーションが正しいという前提がある。
判定対象にある程度の規格があればいいが、「好み」というのは一筋縄ではいかない。この場合は、人によって大きく異なる。ということは、単位空間が安定しないということになる。ここでテクニックになるのだが、「好み」の場合は判定対象のデータだけでなく、判定した人のデータも項目に含めてしまうのである。これで、「このような人ならば、こういうものを好む」という判定が可能になる。明らかに、判定対象のデータだけよりも安定する。
MTSの可能性は広いが、ただのツールとして使わないように。
MTSも品質工学と同様に哲学なのである。
・~・~・~・~・~・~・~・~
<著者 あとがき>
本資料は、20年前に筆者が独自に作成したものに、一部表現の変更、統一を加えたものである。今回、品質工学会からMTSの簡易計算ツールを公開するにあたって、本資料がMTSの中の1つのMT法の基本的な部分を説明しているので、再利用した次第である。
この資料を書いた後、MTA法、TS法、T法、RT法、誤圧などのMTSの派生手法が登場している。公開されたツールはMT法(逆行列)のみなので、他の手法を使いたい場合は、市販されている他のソフトウェアを購入してほしい。
20年前に田口玄一先生とMTSについて将来の展望などについて話したことがある。その際に田口先生が言ったのが「複数のMTSの距離をまとめて、さらにその複数のデータをMTSの距離にして、最終的には人間の脳を再現することまでできるようになる」ということである。当時はビッグデータもAIも話題に上らない時代だったが、そこまで見越してこのような評価システムを作り上げたのは、さすがとしか言いようがない。ただ、20年経過しても、まだこの田口先生の発言を実現できているとは思えない。
ぜひ、このソフトをきっかけとして、MTSを発展させていける人が生まれ、いつか田口先生の発言を現実のものにできる人物が出てくることを期待したい。
最後までお読みいただきありがとうございます。
正直、この文章が多くの人に需要があるとは思っていません。
かなり限られた数人の人、つまりあなたのために書いたと言っても過言ではありません。
ぜひMTシステムを使って、実務で成果を出していただければと思います!
いいなと思ったら応援しよう!

