Pythonを用いた機械学習１４日目

前回からベクトルや行列について学習している。今回は、ベクトルの和と大きさ（①）、ベクトルの内積（②）について学んでいく。

前回の内容はこちらからどうぞ。

１．ベクトルの和と大きさ

ベクトルの足し算は、各要素をそれぞれ足していくだけ。

例題）以下の２つのベクトルの和を求める

解答）

ベクトルの大きさを表すときは、ベクトル記号の両端を「｜」で囲う。ベクトルの大きさは三平方の定理で求められる。

＊NumPyでベクトルの計算を実装するコード

>>> import numpy as np
>>> import math
>>> 
>>> a = np.array([3,2])
>>> b = np.array([1,4])
>>> 
>>> print(a + b)
[4 6]
>>> print(a - b)
[ 2 -2]
>>> print(np.linalg.norm(a))
3.605551275463989
>>> print(np.linalg.norm(b))
4.123105625617661
>>> def norm(x):
...     return math.sqrt(sum([i ** 2 for i in x]))
... 
>>> print(norm(a))
3.605551275463989
>>> print(norm(b))
4.123105625617661
>>>

１〜２行目：ライブラリ（NumPyとMath）をインポート

４〜５行目：ベクトルaとベクトルbを定義

７行目：ベクトルの和を表示

９行目：ベクトルの差を表示

１１行目：ベクトルaの大きさを表示

１３行目：ベクトルbの大きさを表示

１５〜１６行目：各要素の２乗を合計して、その平方根を求める

１８行目：ベクトルaの大きさを表示

２０行目：ベクトルbの大きさを表示

２．ベクトルの内積

中点「・」を使って表記する。以下のようにベクトルaとベクトルbがあった場合、その内積はこのように求められる。

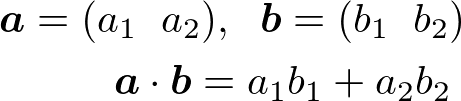
例題）ベクトルaとベクトルbが以下の場合の内積を求める

解答）

（２つのベクトルのなす角が垂直のとき、内積が０となる。内積が正のときは２つのベクトルのなす角が９０度より小さく、内積が負のときは２つのベクトルのなす角が９０度より大きくなる。）

＊NumPyのdot関数を使って内積を計算するコード

>>> import numpy as np
>>> 
>>> a = np.array([3,2])
>>> b = np.array([1,4])
>>> 
>>> print(a.dot(b))
11
>>> c = np.array([2,1])
>>> d = np.array([-1,2])
>>> 
>>> print(c.dot(d))
0
>>> ​
>>> print(b.dot(a))
11
>>> print(d.dot(c))
0
>>> ​

５行目：ベクトルaとベクトルbの内積を表示する

１０行目：ベクトルcとベクトルdの内積を表示する

１３〜１６行目：a.dot(b)のaとbを入れ替えてb.dot(a)としても結果は同じだった。c,dに関しても同様となった。

＊コーシー・シュワルツの不等式

２つのベクトルのなす角で内積の最大と最小を考えられる。これはニューラルネットワークにおいて最小値を求めたい場合に使える。また、次数が増えても同じことが成り立つ。

【TeXclipに関するメモ】

＊\bm{アルファベット}・・・ベクトルを表す太字

TeX/LaTeXの数式アルファベットの太字コマンドまとめ | tm23forest.com

＊\hspace{長さ}・・・横方向のスペース。長さは「数字mm」で書ける。行列の要素間のスペースは2mmで指定している。

＊\cdot・・・中点「・」

＊_（半角アンダーバー）・・・下付き文字

＊\times・・・記号「×」

＊leqq・・・記号「≦」

次回は、多次元のデータを演算していく。