
Photo by
cheemamericco
Pythonを用いた機械学習21日目
前回は、ニューラルネットワークの重みを誤差逆伝播で求めるプログラムを学んだ。今回は、モデル評価についてと練習問題にとり組む。
前回の内容はこちらからどうぞ。
*交差検証
ニューラルネットワークの重みなどのパラメータを学習してテストデータでどれだけ良い結果がでても、実際に使おうとして正しい結果が得られないこともある。そこで、学習したデータと別のデータを使ってその精度を確認する(モデル評価)。
一般的に、与えられたデータを訓練用とテスト用に分けて、訓練用データで学習し、テスト用データでモデル評価を行う。分け方は半分ずつにしたり、7:3や8:3など様々な考え方がある。ただ、分けた際にデータが偏っている可能性もあるので、訓練用データとテストデータを入れ替える「交差検証」を行う。
*過学習と未学習
訓練用データにだけフィットして、テスト用データに対してあまりフィットしない状態を「過学習」といい、一般的なモデルに合わず特殊なデータだけにしか使えない。精度を上げようとして、複雑なモデルを用意しすぎると処理に時間もかかりテストデータへの精度も下がる。
練習問題⑨
scikit-learnのLinearRegressionというモデルを使って、以下のデータに対し、回帰分析と重回帰分析を行い、直線の式を求める。
(scikit-learnはAnacondaでインストールできる)
(1)
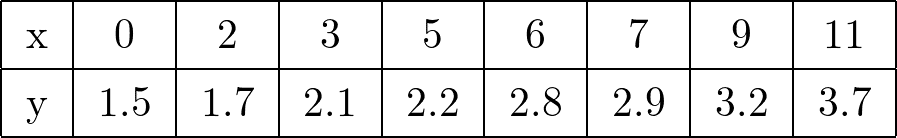
プログラム)
>>> import numpy as np
>>> from sklearn import linear_model
>>> lr = linear_model.LinearRegression()
>>>
>>> x = np.array([[0], [2], [3], [5], [6], [7], [9], [11]])
>>> y = np.array([1.5, 1.7, 2.1, 2.2, 2.8, 2.9, 3.2, 3.7])
>>>
>>> lr.fit(x, y)
>>>
>>> print('coefficient = ', lr.coef_)
coefficient = [0.20519308]
>>>
>>> print('intercept = ', lr.intercept_)
intercept = 1.4095872170439416
>>>
>>> print('y = ', lr.coef_, 'x + ', lr.intercept_)
y = [0.20519308] x + 1.4095872170439416(2)

プログラム)
>>> import numpy as np
>>> from sklearn import linear_model
>>> lr = linear_model.LinearRegression()
>>>
>>> x = np.array([[-2.1, -3.6], [-1.4, 3.1], [0.1, -2.7], [0.8, 1.8], [1.7, -0.5], [3.2, 4.1], [5.7, -1.9], [6.2, 5.2]])
>>> y = np.array([-6.8, 12.2, -8.3, 3.6, -4.8, 5.8, -17.2, 3.1])
>>>
>>> lr.fit(x, y)
>>>
>>> print('回帰係数 = ', lr.coef_)
回帰係数 = [-2.00747629 3.00565224]
>>>
>>> print('切片 = ', lr.intercept_)
切片 = -0.05311549519596337
>>>
>>> print('決定係数', lr.score(x, y))
決定係数 0.9998467355398505
>>>
>>> print('y = ', lr.coef_ [0], 'x1 + ', lr.coef_ [1], 'x2 ', lr.intercept_)
y = -2.007476293890199 x1 + 3.00565224269246 x2 -0.05311549519596337
>>> (3)

プログラム)
>>> import numpy as np
>>> from sklearn import linear_model
>>> lr = linear_model.LinearRegression()
>>>
>>> x = [-3.4, 5.1, 4.1], [-2.2, 3.7, -3.4], [-1.3, -1.6, 2.6], [0.4, 7.3, -1.4], [1.4, -6.1, -3.6], [2.9, 4.2, 3.5], [4.6, 3.9, 2.9], [6.1, 2.5, -1.1]
>>> y = [32.5, 16.1, 2.8, 19.1, -27.1, 4.8, -3.5, -17.5]
>>>
>>> lr.fit(x, y)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
>>>
>>> print('回帰係数 = ', lr.coef_)
回帰係数 = [-3.89668886 2.98806606 0.98281857]
>>>
>>> print('切片 = ', lr.intercept_)
切片 = 0.0013066645356984985
>>>
>>> print('決定係数', lr.score(x, y))
決定係数 0.9999501089821065
>>>
>>> print('y = ', lr.coef_ [0], 'x1 + ', lr.coef_ [1], 'x2 ', lr.coef_ [2], 'x3 + ',lr.intercept_)
y = -3.896688856021157 x1 + 2.9880660582622567 x2 0.982818570253159 x3 + 0.0013066645356984985練習問題⑩
分類問題を学習した結果、テストデータを入れると以下の結果が得られました。このとき、正解率、Aの適合率、Aの再現率、F値をそれぞれ求める。

解答)

*正解率
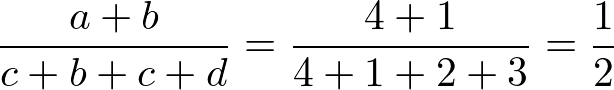
*Aの適合率
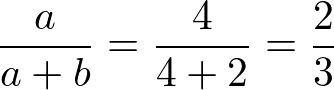
*Aの再現率
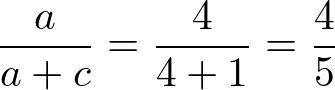
*F値

今回は、学習したモデル評価の方法をざっくりと学んだ。次から、ニューラルネットワークの問題点についてふれていく。
いいなと思ったら応援しよう!

