Pythonを用いた機械学習９日目

機械学習を学ぶ上で欠かせない統計学の知識であるが、今日は前回に引き続き「確率」について学ぶ。同時確率と条件付き確率についてまとめる。

前回の記事はこちら。試行や事象、確率変数や期待値について書いている。

１．同時確率

・「同時確率」・・・２つの事象AとBがあるとき、これらが同時に起こる確率のことであり、下記のように表す

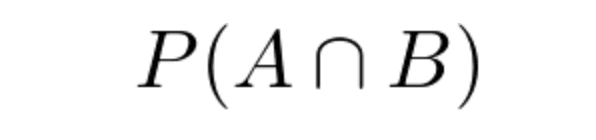
・「A ∩ B」・・・事象A、Bの積事象という

例）２つのサイコロを同時に振ったとき、事象Aは「1つ目のサイコロで偶数がでる」、事象Bは「2つ目のサイコロで3の倍数が出る」とする。このときの分布を「同時確率分布」といい、次の式で求められる。

・「独立」・・・一方の事象がもう一方の事象に影響を与えないこと

独立な事象の場合には、単純に事象の掛け算で積事象を求められる。

先ほどの例の場合は、下のような計算式になる。

２．条件付き確率

・「条件付き確率」・・・ある事象Aが起こったとき、その条件のもとで事象Bが起こる確率のことであり、以下のように表す。

事象Aを全体と考えたときに、事象Bの起こる確率であり、以下のように求めることができる。

また、この式を変形すると、次の確率の乗法定理が得られる。

例）ある夫婦には子どもが二人いる。二人のうち少なくとも一人は男の子であるということが分かった。このとき、二人とも男の子である確率を求めよ。ただし、男の子が生まれる確率、女の子が生まれる確率はともに2分の1とする。

事象Aを「少なくとも一人は男の子」、事象Bを「二人とも男の子」とすると、求める確率は下記のようになる。

事象Aは、４通りの組み合わせから「女女」の１通りを除けばいいので、下記のように表すことができる。

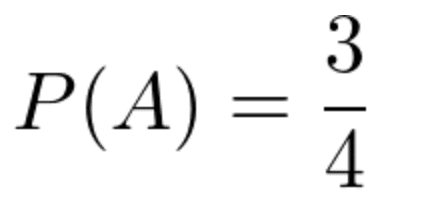
事象Aが起こった上で事象Bが起こるのは下記のようになる。

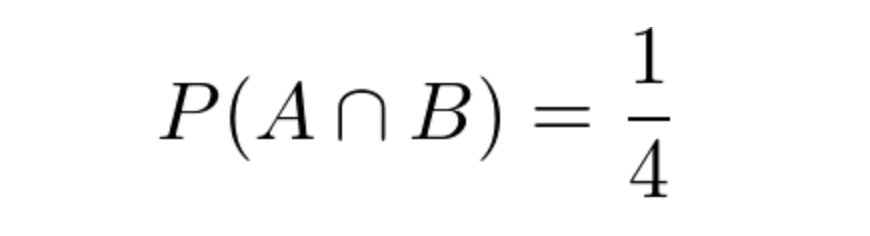
よって、答えは下記のとおり。

例題を解くことで、理解が深まった。同時確率はスッと入ってくるが、条件付き確率はベン図を頭の中で描いて（もしくは実際に書いて）考えたほうが分かりやすい。

次回は、ベイズの定理について学んでいく。

【おまけ：TeXclipメモ】

・記号「 ∩」を描きたいときは、「 \cap」と入力する

・割り算は「\frac{分子}{分母}」

・ブランクを入力したいときは「\hspace{数値mm}」

・記号「μ」は、「\mu」

・記号「λ」は、「\lambda」

・記号「σ」は、「\sigma」