Pythonを用いた機械学習１９日目

今回は回帰分析について学ぶ。

前回の学習内容はこちらからどうぞ。

１．一次関数による予測

例えば、データが一次関数に近いと仮定すると、求める関数はf(x)=ax+bとなる。

一般的なデータはきれいに一次関数に従うわけではなく、誤差が生じる。その誤差を最小にするため、「最小二乗法」をもちいる。

複数のa,bの組み合わせで、(y-f(x))^2を求め、その合計が0になることを理想として、なるべく小さい値をとるようなa,bを求めることが目標になる。

与えられた点をxk,yxであらわすと、n個のデータに対するそれぞれの点における差の合計は下の式（損失関数）であらわすことができる。

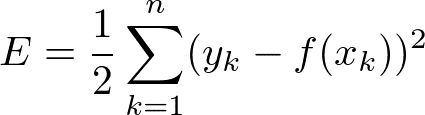
aとbのそれぞれについて偏微分を行う。

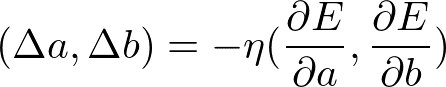
これを連鎖律をもちいて計算すると、

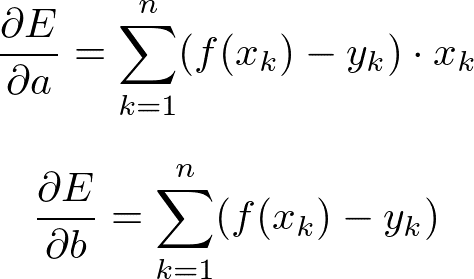
となる。実際にaとbを求めるプログラムで、収束していく様子をみてみる。

＊最小二乗で求めるコード（結果は途中を省略して記載する）

>>> data = [[0, 1.5], [2, 1.7], [3, 2.1], [5, 2.2], [6, 2.8], [7, 2.9], [9, 3.2], [11, 3.7]]
>>> 
>>> def dEa(a, b):
...     sum = 0
...     for i in data:
...         sum += i[0] * (a * i[0] + b - i[1])
...     return sum
... 
>>> def dEb(a, b):
...     sum = 0
...     for i in data:
...         sum += a * i[0] + b - i[1]
...     return sum
... 
>>> eta = 0.006
>>> a, b = 2, 1
>>> 
>>> for i in range(0, 200):
...     a += - eta * dEa(a, b)
...     b += - eta * dEb(a, b)
...     print([a, b])
... 
[-1.3942000000000005, 1.4323036]
[1.7187556712000003, 1.0407140640303998]
[-1.1375221161598432, 1.4048404949261801]
[1.4819971626608965, 1.0756528832032122]
[-0.9216157483942804, 1.3823984078951823]
[1.2826761717376094, 1.1057128320079104]
[-0.7400162738087701, 1.3641628147141933]
[1.1148614539220698, 1.131648744496018]
[-0.5872837573059388, 1.3494488141451413]
[0.9735617753911956, 1.154096333015246]
[-0.45884054053956924, 1.337680568489723]
[0.8545769268422423, 1.1735910540769179]
[-0.350834572451975, 1.3283740031738354]
[0.7543723510105269, 1.1905839844607753]
・・・
[0.20667863633892253, 1.39844083335622]
[0.20665756047211886, 1.3985980227533148]
[0.20663702768113193, 1.3987529645194237]

２．複数変数での重回帰分析

＊ロジスティック回帰・・・ONかOFFかというような、出力が２つの場合に使う。確率を予想するため、結果は0〜1の値をとる。

以下のプログラムで、２つの領域に分ける境界を求めることができる。

＊ロジスティック回帰で求めるコード

>>> import numpy as np
>>> 
>>> data = [[0, 0], [2, 0], [3, 0], [5, 0], [6, 1], [7, 1], [9, 1], [11, 1]]
>>> 
>>> def sigmoid(x):
...     return 1.0 / (1.0 + np.exp(-x))
... 
>>> def dEa(a, b):
...     sum = 0
...     for i in data:
...         sum += i[0] * (sigmoid(a * i[0] + b) - i[1])
...     return sum
... 
>>> def dEb(a, b):
...     sum = 0
...     for i in data:
...         sum += sigmoid(a * i[0] + b) - i[1]
...     return sum
... 
>>> eta = 0.5
>>> a, b = 2, 1
>>> 
>>> for i in range(0, 200):
...     a += - eta * dEa(a, b)
...     b += - eta * dEb(a, b)
...     print([b/a])
... 
[-0.8793427752672711]
[0.04932468721970782]
[-0.13759368177537623]
[-0.8015969222893439]
[0.5381775037301996]
[-0.16494546594290926]
[-0.40230431270027384]
・・・
[-5.536391199787828]
[-5.435947619318161]
[-5.517115685467487]
[-5.452864098059555]
[-5.50412023012486]

一次関数を求める回帰分析と、ロジスティック回帰についてPythonで求める方法を学んだ。次はいよいよニューラルネットワークについて学んでいく。